四川省宜宾市部分中学2022-2023学年高一下学期开学考试数学试题(含答案)
文档属性
| 名称 | 四川省宜宾市部分中学2022-2023学年高一下学期开学考试数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 00:00:00 | ||
图片预览




文档简介
宜宾市部分中学2022-2023学年高一下学期开学考试
数学试题
本试卷共4页,22小题,满分150分。考试用时120分钟。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,,则等于
A. B. C. D.
2.命题“,”的否定是
A., B.,
C., D.,
3.已知函数,则
A.0 B. C. D.1
4.已知扇形面积为8,扇形的圆心角为2 rad,扇形的周长为
A. B. C.8 D.2
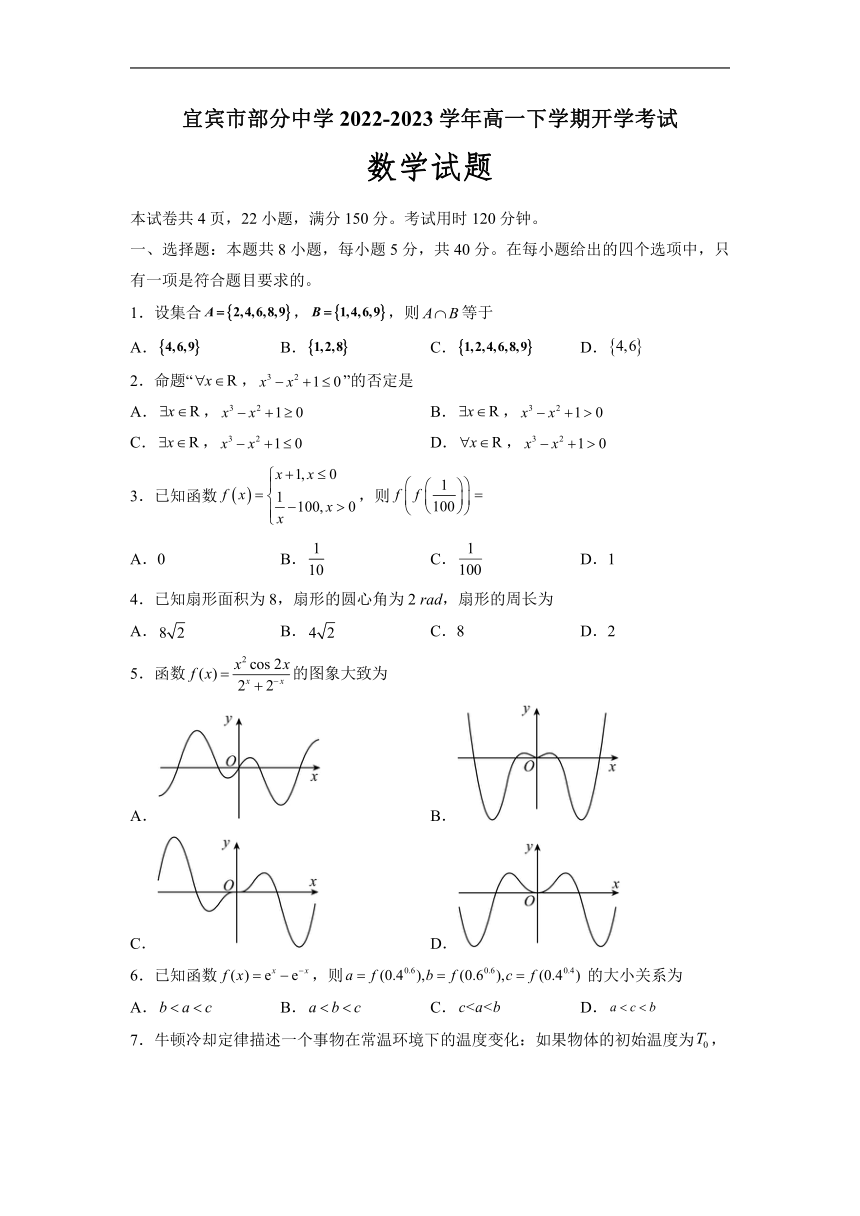
5.函数的图象大致为
A. B.
C. D.
6.已知函数,则的大小关系为
A. B. C. D.
7.牛顿冷却定律描述一个事物在常温环境下的温度变化:如果物体的初始温度为,则经过一定时间后的温度满足,其中是环境温度,称为半衰期,现有一杯80℃的热水用来泡茶,研究表明,此茶的最佳饮用口感会出现在55℃.经测量室温为25℃,茶水降至75℃大约用时1分钟,那么为了获得最佳饮用口感,从泡茶开始大约需要等待( )(参考数据:,,)
A.4分钟 B.5分钟 C.6分钟 D.7分钟
8.已知函数,若方程有六个相异实根,则实数的取值范围
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列四个关系中正确的是
A. B. C. D.
10.若关于的二次不等式的解集为,则下列说法正确的是
A. B.
C.的解集是 D.的解集是
11.下列说法正确的是
A.的最小值是
B.的最小值是
C.的最小值是
D.的最小值是
12.已知函数,,且有最小正零点,若在上单调,则
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13.化简求值:_________.
14.某班有学生45人,参加了数学小组的学生有31人,参加了英语小组的学生有26人.已知该班每个学生都至少参加了这两个小组中的一个小组,则该班学生中既参加了数学小组,又参加了英语小组的学生有___________人.
15.若函数的值域为R,则实数m的取值范围是_________.
16.已知函数的最大值为,最小值为,则的值为____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)(Ⅰ)已知实数满足,求的值.
(Ⅱ)若,求证:.
18.(12分)已知集合,集合.
(Ⅰ)求,;
(Ⅱ)设集合,若,求实数的取值范围.
19.(12分)若,.
(Ⅰ)若的解集为,求的值;
(Ⅱ)求关于的不等式的解集.
20.(12分)已知函数的图象与轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.
(Ⅰ)求的解析式和周期.
(Ⅱ)当时,求的值域.
21.(12分)近年来,我国在航天领域取得了巨大成就,得益于我国先进的运载火箭技术.据了解,在不考虑空气阻力和地球引力的理想状态下,可以用公式计算火箭的最大速度v(单位:).其中(单位)是喷流相对速度,m(单位:)是火箭(除推进剂外)的质量,M(单位:)是推进剂与火箭质量的总和,称为“总质比”.已知A型火箭的喷流相对速度为.
(Ⅰ)当总质比为230时,利用给出的参考数据求A型火箭的最大速度;
(Ⅱ)经过材料更新和技术改进后,A型火箭的喷流相对速度提高到了原来的1.5倍,总质比变为原来的,若要使火箭的最大速度增加,记此时在材料更新和技术改进前的总质比为T,求不小于T的最小整数?
参考数据:
22.(12分)已知,函数.
(Ⅰ)当时,解不等式;
(Ⅱ)若关于的方程有两个不等的实数根,求的取值范围;
(III)设,若对任意,函数在区间上的最大值与最小值的差不超过1,求的取值范围.
宜宾市部分中学2022-2023学年高一下学期开学考试
数学试题参考答案:
A 2.B 3.D 4.A 5.B 6.D 7.C 8.B
9.CD 10.ABC 11.AB 12.BC
13.2 14.12 15. 16.4
17.(1)解:,,,
又,,所以;
(2)证明:设,则且,,,
,,,
,.
18.(1)由,解得,所以,
又在集合中,,∴.
(2)由(1)知
又因为,所以∴,即所以实数的取值范围.
19.(1)的解集为,,1是的解.,.
解得:
(2)当时,不等式的解为,解集为
当时,分解因式
的根为,.
当时,,不等式的解为或;解集为.
当时,,不等式的解为;解集为.
当时,,不等式的解为;等式的解集为.
当时,原不等式为,不等式的解集为.
综上:当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
20.解:(1)由图象上一个最低点为,可得.
又函数的图象与轴的相邻两个交点之间的距离为,
,.
又图象上的一个最低点为,
,
,
又,.
,周期为.
(2)当时,,
又函数在上单调递增,在上单调递减,
故当时,;
当时,.
故函数的值域为.
21.(1)当总质比为230时,,
即A型火箭的最大速度为.
(2)A型火箭的喷流相对速度提高到了原来的1.5倍,所以A型火箭的喷流相对速度为,总质比为,由题意得:
,
因为,
所以,即
不小于T的最小整数为.
22.解:(1)当时,函数,
由不是,可得,则满足,解得或,
即当时,不等式的解集为或.
(2)由题意,关于的方程,
即,可得,
化简得且,
即且,
当时,,不符合题意,舍去;
当时,,不符合题意,舍去,
当且时,,且,
又由,即,解得,
,即,解得,
因为关于的方程有两个不等的实数根,
综上可得且且,
所以实数的取值范围为.
(3)由函数在上单调递减,
因为函数在区间上的最大值与最小值的差不超过1,
可得,即,
即,所以,
设,因为,则,
可得,
当时,,
当时,可得,
因为在区间为单调递减函数,可得,
所以
所以实数的取值范围是.
数学试题
本试卷共4页,22小题,满分150分。考试用时120分钟。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,,则等于
A. B. C. D.
2.命题“,”的否定是
A., B.,
C., D.,
3.已知函数,则
A.0 B. C. D.1
4.已知扇形面积为8,扇形的圆心角为2 rad,扇形的周长为
A. B. C.8 D.2
5.函数的图象大致为
A. B.
C. D.
6.已知函数,则的大小关系为
A. B. C. D.
7.牛顿冷却定律描述一个事物在常温环境下的温度变化:如果物体的初始温度为,则经过一定时间后的温度满足,其中是环境温度,称为半衰期,现有一杯80℃的热水用来泡茶,研究表明,此茶的最佳饮用口感会出现在55℃.经测量室温为25℃,茶水降至75℃大约用时1分钟,那么为了获得最佳饮用口感,从泡茶开始大约需要等待( )(参考数据:,,)
A.4分钟 B.5分钟 C.6分钟 D.7分钟
8.已知函数,若方程有六个相异实根,则实数的取值范围
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列四个关系中正确的是
A. B. C. D.
10.若关于的二次不等式的解集为,则下列说法正确的是
A. B.
C.的解集是 D.的解集是
11.下列说法正确的是
A.的最小值是
B.的最小值是
C.的最小值是
D.的最小值是
12.已知函数,,且有最小正零点,若在上单调,则
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13.化简求值:_________.
14.某班有学生45人,参加了数学小组的学生有31人,参加了英语小组的学生有26人.已知该班每个学生都至少参加了这两个小组中的一个小组,则该班学生中既参加了数学小组,又参加了英语小组的学生有___________人.
15.若函数的值域为R,则实数m的取值范围是_________.
16.已知函数的最大值为,最小值为,则的值为____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)(Ⅰ)已知实数满足,求的值.
(Ⅱ)若,求证:.
18.(12分)已知集合,集合.
(Ⅰ)求,;
(Ⅱ)设集合,若,求实数的取值范围.
19.(12分)若,.
(Ⅰ)若的解集为,求的值;
(Ⅱ)求关于的不等式的解集.
20.(12分)已知函数的图象与轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.
(Ⅰ)求的解析式和周期.
(Ⅱ)当时,求的值域.
21.(12分)近年来,我国在航天领域取得了巨大成就,得益于我国先进的运载火箭技术.据了解,在不考虑空气阻力和地球引力的理想状态下,可以用公式计算火箭的最大速度v(单位:).其中(单位)是喷流相对速度,m(单位:)是火箭(除推进剂外)的质量,M(单位:)是推进剂与火箭质量的总和,称为“总质比”.已知A型火箭的喷流相对速度为.
(Ⅰ)当总质比为230时,利用给出的参考数据求A型火箭的最大速度;
(Ⅱ)经过材料更新和技术改进后,A型火箭的喷流相对速度提高到了原来的1.5倍,总质比变为原来的,若要使火箭的最大速度增加,记此时在材料更新和技术改进前的总质比为T,求不小于T的最小整数?
参考数据:
22.(12分)已知,函数.
(Ⅰ)当时,解不等式;
(Ⅱ)若关于的方程有两个不等的实数根,求的取值范围;
(III)设,若对任意,函数在区间上的最大值与最小值的差不超过1,求的取值范围.
宜宾市部分中学2022-2023学年高一下学期开学考试
数学试题参考答案:
A 2.B 3.D 4.A 5.B 6.D 7.C 8.B
9.CD 10.ABC 11.AB 12.BC
13.2 14.12 15. 16.4
17.(1)解:,,,
又,,所以;
(2)证明:设,则且,,,
,,,
,.
18.(1)由,解得,所以,
又在集合中,,∴.
(2)由(1)知
又因为,所以∴,即所以实数的取值范围.
19.(1)的解集为,,1是的解.,.
解得:
(2)当时,不等式的解为,解集为
当时,分解因式
的根为,.
当时,,不等式的解为或;解集为.
当时,,不等式的解为;解集为.
当时,,不等式的解为;等式的解集为.
当时,原不等式为,不等式的解集为.
综上:当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
20.解:(1)由图象上一个最低点为,可得.
又函数的图象与轴的相邻两个交点之间的距离为,
,.
又图象上的一个最低点为,
,
,
又,.
,周期为.
(2)当时,,
又函数在上单调递增,在上单调递减,
故当时,;
当时,.
故函数的值域为.
21.(1)当总质比为230时,,
即A型火箭的最大速度为.
(2)A型火箭的喷流相对速度提高到了原来的1.5倍,所以A型火箭的喷流相对速度为,总质比为,由题意得:
,
因为,
所以,即
不小于T的最小整数为.
22.解:(1)当时,函数,
由不是,可得,则满足,解得或,
即当时,不等式的解集为或.
(2)由题意,关于的方程,
即,可得,
化简得且,
即且,
当时,,不符合题意,舍去;
当时,,不符合题意,舍去,
当且时,,且,
又由,即,解得,
,即,解得,
因为关于的方程有两个不等的实数根,
综上可得且且,
所以实数的取值范围为.
(3)由函数在上单调递减,
因为函数在区间上的最大值与最小值的差不超过1,
可得,即,
即,所以,
设,因为,则,
可得,
当时,,
当时,可得,
因为在区间为单调递减函数,可得,
所以
所以实数的取值范围是.
同课章节目录
