2022-2023学年苏科数学七年级下册 第七章 平面图形的认识(二)课后作业(共10份含答案)
文档属性
| 名称 | 2022-2023学年苏科数学七年级下册 第七章 平面图形的认识(二)课后作业(共10份含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 418.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 17:24:24 | ||
图片预览



文档简介
第7章 平面图形的认识(二)
7.1 探索直线平行的条件(1)
班级:___________ 姓名:____________
应知应会
1.如图,图形中不是同位角的是 ( )
A.∠3与∠6 B.∠4与∠7 C.∠1与∠5 D.∠2与∠5
(
(第
4
题)
) (
(第
2
题)
) (
(第
1
题)
)
(
(第
3
题)
)
2.如图,下列条件能判定的是 ( )
A.∠1=∠2 B.∠1=∠4 C.∠3=∠5 D.∠3=∠4
3.对于图中标记的各角,下列条件能够推理得到a∥b的是 ( )
A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠2+∠3=∠4
4.如图,请填写一个条件,使结论成立:∵__________,∴.
5.如图∵,
∴
( )
∵,
(
(第
5
题)
)∴
( )
巩固提升
6.如图,分别找出图中∠3的同位角,∠2的同位角,∠B的同位角.
(
(第
6
题)
)∠3的同位角:
_____________________________________________
∠2的同位角:
_____________________________________________
∠B的同位角:
_____________________________________________
拓展优化
7.如图,直线a、b被直线c所截,∠1=∠3,直线a与直线b平行吗?为什么?
(
(第
7
题)
)
(
等第:
时间
:
)
7.1 探索直线平行的条件(2)
班级:___________ 姓名:____________
应知应会
1.如图,∠1和∠2是直线 和直线 被直线 所截得到的 应选 ( )
A.a,b,c,同旁内角 B.a,c,b,同位角
C.a,b,c,同位角 D.c,b,a,同位角
(
(第
2
题)
) (
(第
1
题)
)
(
(第
4
题)
) (
(第
3
题)
)
2.如图所示,下列说法中,错误的是 ( )
A.∠A与∠EDC是同位角 B.∠A与∠C是同旁内角
C.∠A与∠ADC是同旁内角 D.∠A与∠ABF是内错角
3.如图,下列推理正确的是 ( )
A.∵∠BAD+∠ABC=180°,∴AB∥CD B.∵∠BAD+∠ADC=180°,∴AD∥BC
C.∵∠2=∠4,∴AD∥BC D.∵∠1=∠3,∴AD∥BC
巩固提升
4.如图,将两个含30°角的直角三角板的最长边靠在一起滑动,可知直角边AB∥CD,依据是 .
5.如图,AE平分∠BAC,CE平分∠ACD,有下列条件:∠1=∠2;∠1+∠2=90°;
∠3+∠4=90°;∠2+∠3=90°;其中能判定AB∥CD的有 个
(
(第
5
题)
)拓展优化
6.将一副三角板中的两个直角顶点C叠放在一起(如图①),
其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)若∠BCD=150°,求∠ACE的度数;
(2)试猜想∠BCD与∠ACE的数量关系,请说明理由;
(
(第
6
题)
)(3)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时,CD∥AB,并简要说明理由.
(
等第:
时间
:
)
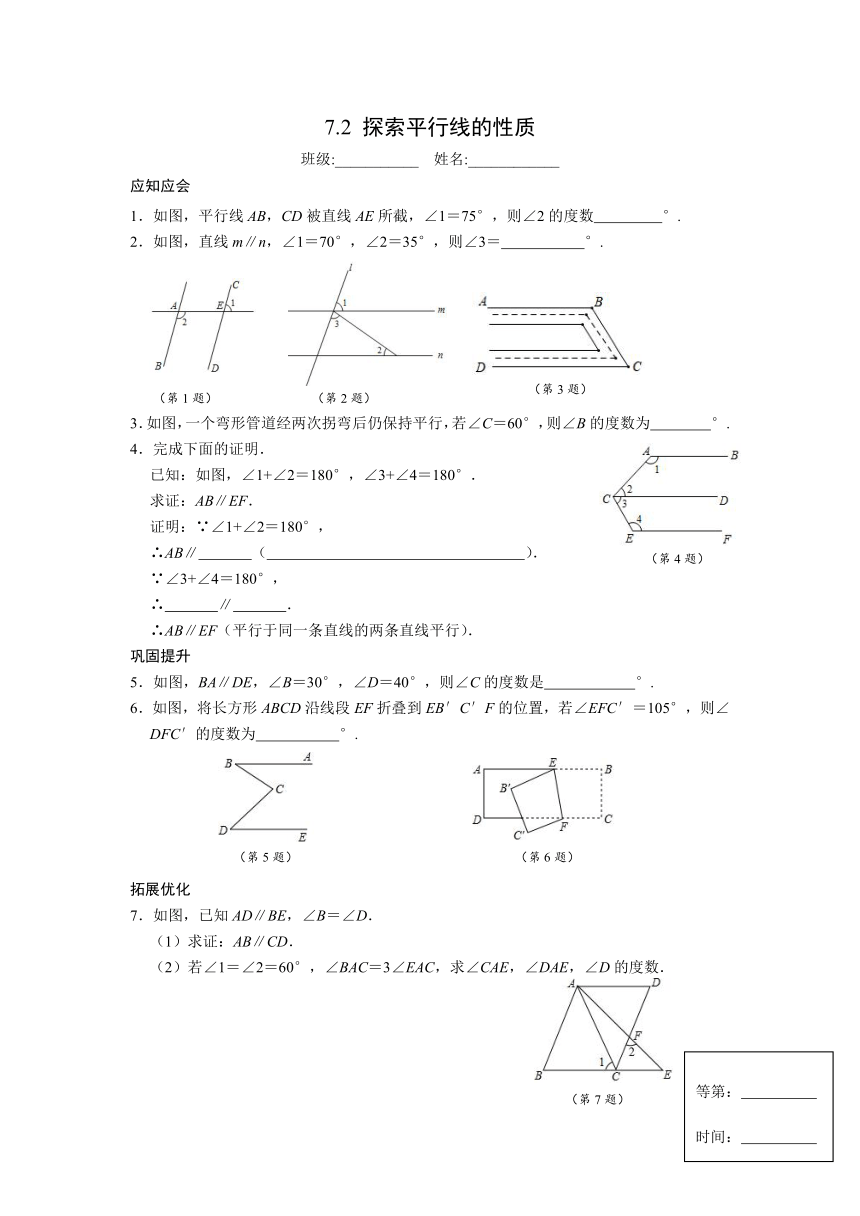
7.2 探索平行线的性质
班级:___________ 姓名:____________
应知应会
1.如图,平行线AB,CD被直线AE所截,∠1=75°,则∠2的度数 °.
2.如图,直线m∥n,∠1=70°,∠2=35°,则∠3= °.
(
(第
2
题)
) (
(第
1
题)
)
(
(第
3
题)
)
(
(第
4
题)
)3.如图,一个弯形管道经两次拐弯后仍保持平行,若∠C=60°,则∠B的度数为 °.
4.完成下面的证明.
已知:如图,∠1+∠2=180°,∠3+∠4=180°.
求证:AB∥EF.
证明:∵∠1+∠2=180°,
∴AB∥ ( ).
∵∠3+∠4=180°,
∴ ∥ .
∴AB∥EF(平行于同一条直线的两条直线平行).
巩固提升
5.如图,BA∥DE,∠B=30°,∠D=40°,则∠C的度数是 °.
6.如图,将长方形ABCD沿线段EF折叠到EB′C′F的位置,若∠EFC′=105°,则∠DFC′的度数为 °.
(
(第
6
题)
) (
(第
5
题)
)
拓展优化
7.如图,已知AD∥BE,∠B=∠D.
(1)求证:AB∥CD.
(
(第
7
题)
)(2)若∠1=∠2=60°,∠BAC=3∠EAC,求∠CAE,∠DAE,∠D的度数.
(
等第:
时间
:
)
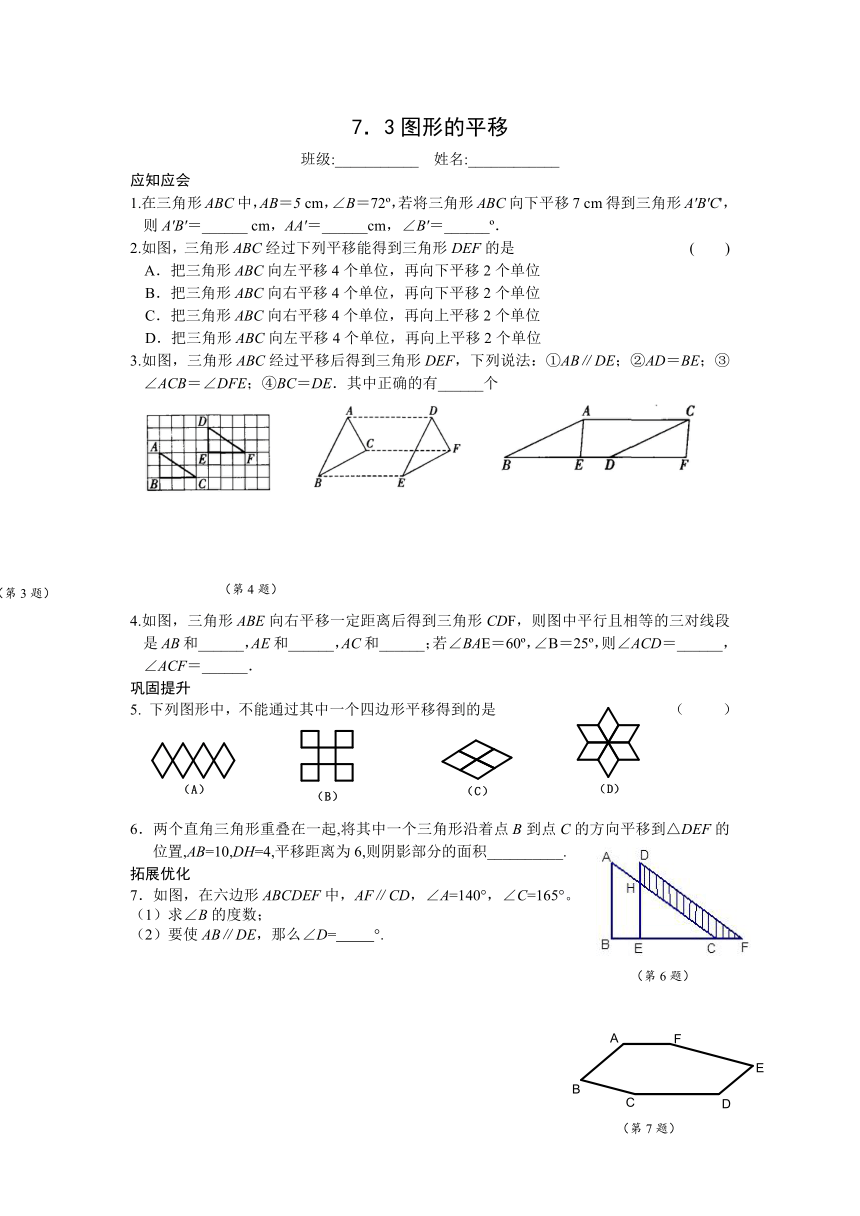
7.3图形的平移
班级:___________ 姓名:____________
应知应会
1.在三角形ABC中,AB=5 cm,∠B=72 ,若将三角形ABC向下平移7 cm得到三角形A'B'C',则A'B'=______ cm,AA'=______cm,∠B'=______ .
2.如图,三角形ABC经过下列平移能得到三角形DEF的是 ( )
A.把三角形ABC向左平移4个单位,再向下平移2个单位
B.把三角形ABC向右平移4个单位,再向下平移2个单位
C.把三角形ABC向右平移4个单位,再向上平移2个单位
D.把三角形ABC向左平移4个单位,再向上平移2个单位
3.如图,三角形ABC经过平移后得到三角形DEF,下列说法:①AB∥DE;②AD=BE;③∠ACB=∠DFE;④BC=DE.其中正确的有______个
(
(第
3
题)
) (
(第
4
题)
) (
(第
2
题)
)
4.如图,三角形ABE向右平移一定距离后得到三角形CDF,则图中平行且相等的三对线段是AB和______,AE和______,AC和______;若∠BAE=60 ,∠B=25 ,则∠ACD=______,∠ACF=______.
巩固提升
5. 下列图形中,不能通过其中一个四边形平移得到的是 ( )
(
(第
6
题)
)6.两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分的面积__________.
拓展优化
7.如图,在六边形ABCDEF中,AF∥CD,∠A=140°,∠C=165°。
(1)求∠B的度数;
(2)要使AB∥DE,那么∠D= °.
(
(第
7
题)
)
(
等第:
时间
:
)
7.4认识三角形(1)
班级:___________ 姓名:____________
应知应会
1.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是 ( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.5cm,5cm,11cm D.13cm,12cm,20cm
2.小李有2根木棒,长度分别为10cm和15cm,要组成一个三角形(木棒的首尾分别连接),还需在下列4根木棒中选取 ( )
A.4cm长的木棒 B.5cm长的木棒 C.20cm长的木棒 D.25cm长的木棒
3.现有四根木棒,长度分别为4 cm、6 cm、8 cm、10 cm.从中任取三根木棒,能组成三角形的个数为 ( )
A.1 B.2 C.3 D.4
4.(1)如图,点D在△ABC中,写出图中所有三角形: ;
(2)如图,线段BC是△ 和△ 的边;
(3)如图,△ABD的3个内角是 ,三条边是 .
5.如图,D是△ABC的边BC上的一点,则在△ABC中∠C所对的边是 ,在△ACD中∠C所对的边是 ,在△ABD中边AD所对的角是 ,在在△ACD中边AD所对的角是 。
(
(第
6
题)
) (
(第
5
题)
) (
(第
4
题)
)
6.图中有 个三角形,其中,
是锐角三角形,
是直角三角形,
是钝角三角形。
7.已知三角形的三边长为3,5,x,则第三边x的取值范围是 .
8.等腰三角形的两边长分别为4和6,则这个等腰三角形的周长是 .
9.三角形的边长都是整数,并且唯一的最长边是6,则这样的三角形共有 个.
巩固提升
10.等腰三角形的两条边长分别为6 cm和7 cm,当周长为偶数时,第三边的长度为______cm.
11.已知a、b、c是一个三角形的三条边长,则______.
拓展优化
12.已知等腰三角形的周长为14cm,底边与腰的比为3:2,求各边的长.
(
等第:
时间
:
)
7.4认识三角形(2)
班级:___________ 姓名:____________
应知应会
1.下列说法正确的是 ( )
A.三角形的角平分线、中线、高都在三角形的内部 B.直角三角形只有一条高
C.三角形的三条高至少有一条在三角形内 D.钝角三角形的三条高均在三角形外
2.如图,△ABC的角平分线AD、中线BE相交于点O,则①AO是△ABE的角平分线,②BO是△ABD的中线的结论中 ( )
A.①正确,②不正确 B.①不正确,②正确 C.①和②都正确 D.①和②都不正确
(
(第
2
题)
) (
(第
4
题)
)
3.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是 ( )
A. B. C. D.
4.如图,AD是△ABC的中线,AE、AF分别是△BAD、△CAD的角平分线,且∠BAC=90 ,则 (1)BD=______=______; (2) ∠BAE=∠______=______;
(3) ∠______=∠______=∠DAC; (4) ∠EAF=∠______.
(
(第
5
题)
)5.如图,AD、AE分别是△ABC的中线和高,BC=6 cm,AE=4 cm
(1)求△ABC、△ABD和△ADC的面积;(2)你能得出什么结论?
巩固提升
6..如图,在△ABC中,D、E分别为BC、AD的中点,且S△ABC=4,则S阴影为 ( )
A.2 B.1 C. D.
(
(第
7
题)
(第
6
题)
)
拓展优化
(
等第:
时间
:
)7.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADC的面积为S1,△ACE的面积为S2,若S△ABC=6,则S1﹣S2的值为 .
7.5 多边形的内角和与外角和(1)
班级:___________ 姓名:____________
应知应会
1.一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺
前的∠C的度数为 ( )
A.75° B.60° C.45° D.40°
2.如图,在△ABC中,AD平分∠BAC,∠C=30°,∠DAC=45°,则∠B的度数为 °.
3.如图,∠A=∠C=90°,AD、BC交于点E,∠2=25°,则∠1的值为 °.
(
(第
4
题)
) (
(第
3
题)
) (
(第
2
题)
) (
(第
1
题)
)
4.如图,△ABC,∠B、∠C的平分线BE,CD交于点F,若∠BFC=116°,则∠A= °.
5. 已知△ABC中,∠A=30°,∠C=2∠B,则∠B= °.
巩固提升
6. 如图,在△ABC中,∠ABC=80°,∠C=70°,且BE∥AC,则∠EBD= °.
7. 如图,在△ABC中,AD是∠BAC的平分线,E为AD上一点,且EF⊥BC于点F,若∠C=35°,∠DEF=15°,则∠B的度数为 °.
(
(第
7
题)
) (
(第
6
题)
)
拓展优化
8. 如图,在△ABC中,∠ABC=56°,∠ACB=44°,AD是BC边上的高,AE是△ABC的平分线,求∠DAE的度数.
(
(第
8
题)
)
(
等第:
时间
:
)
7.5 多边形的内角和与外角和(2)
班级:___________ 姓名:____________
应知应会
1.七边形的内角和为 °.
2.如图所示,∠B的值为 °.
3.如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为 °.
4.一个多边形的每个内角均为150°,则这个多边形是 边形
(
(第
7
题)
) (
(第
5
题)
) (
(第
3
题)
) (
(第
2
题)
)
5.如图,在五边形ABCDE中,∠A+∠B+∠E=320°,DP、CP分别平分∠EDC、∠BCD,则∠CPD的度数是 °.
6.在四边形ABCD中,∠A:∠B:∠C:∠D=2:3:4:6,则∠B的度数是 °.
巩固提升
7.如图,多边形ABCDEFG中,∠E=∠F=∠G=108°,∠C=∠D=72°,则∠A+∠B的值为 °.
8.如图,五边形ABCDE的每个内角都相等,已知EF⊥BC,求证:EF平分∠AED.
(
(第
8
题)
)
拓展优化
9.如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,
将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC.
求:(1)∠F的度数;(2)∠D的度数.
(
等第:
时间
:
)
(
(第
9
题)
)
7.5 多边形的内角和与外角和(3)
班级:___________ 姓名:____________
应知应会
1.六边形的外角和为 °.
2.若n边形的内角和等于外角和的3倍,则边数n为 .
3.若一个多边形的每一个外角都等于36°,则这个多边形的内角和为 °.
4.若一个多边形的内角和与外角和总共是900°,则此多边形是 边形
5.一个多边形的边数每增加一条,这个多边形的 ( )
A.内角和增加360° B.外角和增加360° C.内角和增加180° D.对角线增加一条
巩固提升
6.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于 °.
7.如图,把△ABC纸片沿DE折叠,使点A落在图中的A'处,若∠A=25°,∠BDA'=120°,则∠A'EC= °.
(
(第
7
题)
) (
(第
6
题)
)
拓展优化
8.如图①,∠1、∠2是四边形ABCD的两个不相邻的外角.
(1)猜想并说明∠1+∠2与∠A、∠C的数量关系;
(2)如图②,在四边形ABCD中,∠ABC与∠ADC的平分线交于点O.若∠A=50°,
∠C=150°,求∠BOD的度数;
(3)如图③,BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线.请直接写出∠A、∠C与∠O的的数量关系 .
(
等第:
时间
:
)
第7章 单元测过关
(时间:60分钟 满分:150分)
班级:___________ 姓名:____________
一、选择题(每题4分,共32分)
1.把右边如图所示的海豚吉祥物进行平移,能得到的图形是 ( )
A. B. C. D.
2.用下列长度的三根木棒首尾相接,能做成三角形框架的是 ( )
A.2cm,2cm,4cm B.3cm,4cm,5cm C.1cm,2cm,3cm D.2cm,3cm,6cm
3.如图,能判断AB∥CD的条件是 ( )
A.∠A=∠DCE B.∠A=∠ACD C.∠B=∠ACB D.∠B=∠ACD
4.如图所示,AB∥CD,∠A=50°,∠C=27°,则∠AEC的大小应为 ( )
A.23° B.70° C.77° D.80°
5.如图,将一副直角三角板按照图中所示位置摆放,点E在边AB上,两条斜边互相平行,
∠DEF=∠ABC=90°,∠A=30°,∠D=45°,则∠AED等于 ( )
(
(第
3
题)
(第
4
题)
(第
5
题)
(第
7
题)
)A.15° B.20° C.25° D.30°
(
(第
8
题)
)6.列说法中错误的是 ( )
A.三角形的一个外角大于任何一个内角
B.有一个内角是直角的三角形是直角三角形
C.任意三角形的外角和都是360°
D.三角形的中线、角平分线,高线都是线段
7.如图,五边形ABCDE的一个内角∠A=110°,则∠1+∠2+∠3+∠4等于 ( )
A.360° B.290° C.270° D.250°
8.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,
GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
二、填空题(每题4分,共40分)
9.在△ABC中,∠A=36°,∠B=∠C,则∠B= °.
10.一个多边形的内角和为2700°,则这个多边形的边数是 边.
11.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为 °.
12.一架飞机向北飞行,两次改变方向后,前进的方向与原来的航行方向平行,已知第一次向
左拐50°,那么第二次向右拐 。
13. 如图,△ABC沿BC方向平移4cm得到△DEF,如果四边形ABFD的周长是32cm,则△DEF的周长是 cm.
(
(第
11
题)
(第
13
题)
(第
14
题)
)14. 如图,六边形ABCDEF的各角都相等,若m∥n,则∠1+∠2= °.
15.如图,三角形纸片ABC中∠A=66°,∠B=73°,将纸片一角折叠,使点C落在△ABC的内部C′处,若∠2=55°,则∠1= .
16.如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,
④∠D=∠ACB,正确的有结论有 个.
17.如图所示,分别以五边形ABCDE的顶点为圆心,以单位1为半径画圆,则图中阴影
(
(第
16
题)
(第
15
题)
(第
17
题)
)部分的面积之和为 平方单位.
18.定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为30°,那么这个“特征角”α的度数为 °.
三、解答题(共78分)
19.(满分8分) 如图在方格纸中,△ABC的顶点都在方格纸的格点上.
(1)将△ABC平移后得到△A′B′C′,图中已画出B点
的对应点B′,请补全△A′B′C′;
(2)画出△A′B′C′的高C′H以及中线A′D;
(3)直接写出BB′和CC′的数量关系: .
20. (满分8分)已知:如图,DE∥BC,BE平分∠ABC.已知∠1=35°.求∠3的度数.
21. (满分8分)如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,∠1=∠2,问AF与BC有怎样的位置关系?为什么?
22. (满分12分)如图,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1=48°,求∠2的度数;
(2)求证:AB∥DE.
23. (满分12分)如图,AH⊥BC于点H,点D,E分别在AB,AC上,DF⊥BC于F.
∠B=55°,∠1=35°.
(1)求证:EH∥AB.
(2)求∠2的度数.
24. (满分14分)如图,在四边形ABCD中,∠A与∠C互补,∠ABC、∠ADC的平分线分别交CD、AB于点E、F.EG∥AB,交BC于点G.
(1)∠1与∠2有怎样的数量关系?为什么?
(2)若∠A=100°,∠1=42°,求∠CEG的度数.
25.(满分16分)∠MOQ=90°,点A,B分别在射线OM、OQ上运动(不与点O重合).
(1)如图1,AI平分∠BAO,BI平分∠ABO,若∠BAO=40°,则∠AIB= °;
(2)如图2,AI平分∠BAO,BC平分∠ABM,BC的反向延长线交AI于点D.
①若∠BAO=40°,则∠ADB= °;
②点A、B在运动的过程中,∠ADB是否发生变化,若不变,试求∠ADB的度数;若变化,请说明变化规律.
(3)如图3,已知点E在BA的延长线上,∠BAO的角平分线AI、∠OAE的角平分线AF
与∠BOP的角平分线所在的直线分别相交于的点D、F,在△ADF中,如果有一个角的
度数是另一个角的4倍,请直接写出∠ABO的度数.
参考答案:
第7章 单元测过关
1.C. 2.B. 3.B. 4.C. 5.A. 6.A. 7.B. 8.C. 9. 72. 10. 17. 11. 130. 12. 50. 13. 24. 14. 180. 15. 27. 16. 3. 17. π. 18. 30°、60°或100°. 19. (1)如图,△A′B′C′即为所求;
(2)高C′H、中线A′D即为所求;(3)BB′和CC′的数量关系为:相等. 20. ∵因为DE∥BC,∴所以∠2=∠3,∵因为BE平分∠ABC,∴所以∠1=∠2,∴所以∠3=∠1=35°.21. AF与BC的位置关系是平行,理由如下:因为DE∥AC,所以∠1=∠C,因为∠1=∠2,所以∠C=∠2,所以AF∥BC. 22. (1)因为六边形ABCDEF的各内角相等,所以一个内角的大小为,所以∠E=∠F=∠BAF=120°.因为∠FAB=120°,∠1=48°,所以∠FAD=∠FAB﹣∠DAB=120°﹣48°=72°.因为∠2+∠FAD+∠F+∠E=360°,∠F=∠E=120°,所以∠ADE=360°﹣∠FAD﹣∠F﹣∠E=360°﹣72°﹣120°﹣120°=48°;(2)证明:因为∠1=120°﹣∠DAF,∠2=360°﹣120°﹣120°﹣∠DAF=120°﹣∠DAF,所以∠1=∠2,所以AB∥DE. 23. (1)因为AH⊥BC,所以∠AHC=90°,因为∠1=35°.所以∠EHC=55°,因为∠B=55°,所以∠B=∠3,所以EH∥AB(同位角相等,两直线平行).(2)因为EH∥AB,所以∠1=∠BAH=35°(两直线平行,内错角相等),因为AH⊥BC,DF⊥BC,所以AH∥DF,所以∠2+∠BAH=180°(两直线平行,同旁内角互补),所以∠2=145°. 24. (1)∠1与∠2互余.因为四边形ABCD的内角和为360°,∠A与∠C互补,所以∠ABC+∠ADC=360°﹣180°=180°,因为BE、DF分别平分∠ABC、∠ADC,所以,,因为EG∥AB,所以∠2=∠ABE,所以∠1+∠2=,即∠1与∠2互余;(2)因为∠A=100°,∠1=42°,所以∠C=80°,∠2=48°,所以∠ABE=∠CBE=48°,所以∠BEC=180°﹣48°﹣80°=52°,所以∠CEG=52°﹣48°=4°.25. (1)135°;(2)如图2中,①45;②不变,理由:因为∠D=∠CBA﹣∠BAD=∠MBA﹣∠BAO=(∠MBA﹣∠BAO)=∠AOB=×90°=45°,所以点A、B在运动的过程中,∠ADB=45°.(3)当∠ABO=45°或36°时,在△ADF中,有一个角的度数是另一个角的4倍.
7.1 探索直线平行的条件(1)
班级:___________ 姓名:____________
应知应会
1.如图,图形中不是同位角的是 ( )
A.∠3与∠6 B.∠4与∠7 C.∠1与∠5 D.∠2与∠5
(
(第
4
题)
) (
(第
2
题)
) (
(第
1
题)
)
(
(第
3
题)
)
2.如图,下列条件能判定的是 ( )
A.∠1=∠2 B.∠1=∠4 C.∠3=∠5 D.∠3=∠4
3.对于图中标记的各角,下列条件能够推理得到a∥b的是 ( )
A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠2+∠3=∠4
4.如图,请填写一个条件,使结论成立:∵__________,∴.
5.如图∵,
∴
( )
∵,
(
(第
5
题)
)∴
( )
巩固提升
6.如图,分别找出图中∠3的同位角,∠2的同位角,∠B的同位角.
(
(第
6
题)
)∠3的同位角:
_____________________________________________
∠2的同位角:
_____________________________________________
∠B的同位角:
_____________________________________________
拓展优化
7.如图,直线a、b被直线c所截,∠1=∠3,直线a与直线b平行吗?为什么?
(
(第
7
题)
)
(
等第:
时间
:
)
7.1 探索直线平行的条件(2)
班级:___________ 姓名:____________
应知应会
1.如图,∠1和∠2是直线 和直线 被直线 所截得到的 应选 ( )
A.a,b,c,同旁内角 B.a,c,b,同位角
C.a,b,c,同位角 D.c,b,a,同位角
(
(第
2
题)
) (
(第
1
题)
)
(
(第
4
题)
) (
(第
3
题)
)
2.如图所示,下列说法中,错误的是 ( )
A.∠A与∠EDC是同位角 B.∠A与∠C是同旁内角
C.∠A与∠ADC是同旁内角 D.∠A与∠ABF是内错角
3.如图,下列推理正确的是 ( )
A.∵∠BAD+∠ABC=180°,∴AB∥CD B.∵∠BAD+∠ADC=180°,∴AD∥BC
C.∵∠2=∠4,∴AD∥BC D.∵∠1=∠3,∴AD∥BC
巩固提升
4.如图,将两个含30°角的直角三角板的最长边靠在一起滑动,可知直角边AB∥CD,依据是 .
5.如图,AE平分∠BAC,CE平分∠ACD,有下列条件:∠1=∠2;∠1+∠2=90°;
∠3+∠4=90°;∠2+∠3=90°;其中能判定AB∥CD的有 个
(
(第
5
题)
)拓展优化
6.将一副三角板中的两个直角顶点C叠放在一起(如图①),
其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)若∠BCD=150°,求∠ACE的度数;
(2)试猜想∠BCD与∠ACE的数量关系,请说明理由;
(
(第
6
题)
)(3)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时,CD∥AB,并简要说明理由.
(
等第:
时间
:
)
7.2 探索平行线的性质
班级:___________ 姓名:____________
应知应会
1.如图,平行线AB,CD被直线AE所截,∠1=75°,则∠2的度数 °.
2.如图,直线m∥n,∠1=70°,∠2=35°,则∠3= °.
(
(第
2
题)
) (
(第
1
题)
)
(
(第
3
题)
)
(
(第
4
题)
)3.如图,一个弯形管道经两次拐弯后仍保持平行,若∠C=60°,则∠B的度数为 °.
4.完成下面的证明.
已知:如图,∠1+∠2=180°,∠3+∠4=180°.
求证:AB∥EF.
证明:∵∠1+∠2=180°,
∴AB∥ ( ).
∵∠3+∠4=180°,
∴ ∥ .
∴AB∥EF(平行于同一条直线的两条直线平行).
巩固提升
5.如图,BA∥DE,∠B=30°,∠D=40°,则∠C的度数是 °.
6.如图,将长方形ABCD沿线段EF折叠到EB′C′F的位置,若∠EFC′=105°,则∠DFC′的度数为 °.
(
(第
6
题)
) (
(第
5
题)
)
拓展优化
7.如图,已知AD∥BE,∠B=∠D.
(1)求证:AB∥CD.
(
(第
7
题)
)(2)若∠1=∠2=60°,∠BAC=3∠EAC,求∠CAE,∠DAE,∠D的度数.
(
等第:
时间
:
)
7.3图形的平移
班级:___________ 姓名:____________
应知应会
1.在三角形ABC中,AB=5 cm,∠B=72 ,若将三角形ABC向下平移7 cm得到三角形A'B'C',则A'B'=______ cm,AA'=______cm,∠B'=______ .
2.如图,三角形ABC经过下列平移能得到三角形DEF的是 ( )
A.把三角形ABC向左平移4个单位,再向下平移2个单位
B.把三角形ABC向右平移4个单位,再向下平移2个单位
C.把三角形ABC向右平移4个单位,再向上平移2个单位
D.把三角形ABC向左平移4个单位,再向上平移2个单位
3.如图,三角形ABC经过平移后得到三角形DEF,下列说法:①AB∥DE;②AD=BE;③∠ACB=∠DFE;④BC=DE.其中正确的有______个
(
(第
3
题)
) (
(第
4
题)
) (
(第
2
题)
)
4.如图,三角形ABE向右平移一定距离后得到三角形CDF,则图中平行且相等的三对线段是AB和______,AE和______,AC和______;若∠BAE=60 ,∠B=25 ,则∠ACD=______,∠ACF=______.
巩固提升
5. 下列图形中,不能通过其中一个四边形平移得到的是 ( )
(
(第
6
题)
)6.两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分的面积__________.
拓展优化
7.如图,在六边形ABCDEF中,AF∥CD,∠A=140°,∠C=165°。
(1)求∠B的度数;
(2)要使AB∥DE,那么∠D= °.
(
(第
7
题)
)
(
等第:
时间
:
)
7.4认识三角形(1)
班级:___________ 姓名:____________
应知应会
1.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是 ( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.5cm,5cm,11cm D.13cm,12cm,20cm
2.小李有2根木棒,长度分别为10cm和15cm,要组成一个三角形(木棒的首尾分别连接),还需在下列4根木棒中选取 ( )
A.4cm长的木棒 B.5cm长的木棒 C.20cm长的木棒 D.25cm长的木棒
3.现有四根木棒,长度分别为4 cm、6 cm、8 cm、10 cm.从中任取三根木棒,能组成三角形的个数为 ( )
A.1 B.2 C.3 D.4
4.(1)如图,点D在△ABC中,写出图中所有三角形: ;
(2)如图,线段BC是△ 和△ 的边;
(3)如图,△ABD的3个内角是 ,三条边是 .
5.如图,D是△ABC的边BC上的一点,则在△ABC中∠C所对的边是 ,在△ACD中∠C所对的边是 ,在△ABD中边AD所对的角是 ,在在△ACD中边AD所对的角是 。
(
(第
6
题)
) (
(第
5
题)
) (
(第
4
题)
)
6.图中有 个三角形,其中,
是锐角三角形,
是直角三角形,
是钝角三角形。
7.已知三角形的三边长为3,5,x,则第三边x的取值范围是 .
8.等腰三角形的两边长分别为4和6,则这个等腰三角形的周长是 .
9.三角形的边长都是整数,并且唯一的最长边是6,则这样的三角形共有 个.
巩固提升
10.等腰三角形的两条边长分别为6 cm和7 cm,当周长为偶数时,第三边的长度为______cm.
11.已知a、b、c是一个三角形的三条边长,则______.
拓展优化
12.已知等腰三角形的周长为14cm,底边与腰的比为3:2,求各边的长.
(
等第:
时间
:
)
7.4认识三角形(2)
班级:___________ 姓名:____________
应知应会
1.下列说法正确的是 ( )
A.三角形的角平分线、中线、高都在三角形的内部 B.直角三角形只有一条高
C.三角形的三条高至少有一条在三角形内 D.钝角三角形的三条高均在三角形外
2.如图,△ABC的角平分线AD、中线BE相交于点O,则①AO是△ABE的角平分线,②BO是△ABD的中线的结论中 ( )
A.①正确,②不正确 B.①不正确,②正确 C.①和②都正确 D.①和②都不正确
(
(第
2
题)
) (
(第
4
题)
)
3.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是 ( )
A. B. C. D.
4.如图,AD是△ABC的中线,AE、AF分别是△BAD、△CAD的角平分线,且∠BAC=90 ,则 (1)BD=______=______; (2) ∠BAE=∠______=______;
(3) ∠______=∠______=∠DAC; (4) ∠EAF=∠______.
(
(第
5
题)
)5.如图,AD、AE分别是△ABC的中线和高,BC=6 cm,AE=4 cm
(1)求△ABC、△ABD和△ADC的面积;(2)你能得出什么结论?
巩固提升
6..如图,在△ABC中,D、E分别为BC、AD的中点,且S△ABC=4,则S阴影为 ( )
A.2 B.1 C. D.
(
(第
7
题)
(第
6
题)
)
拓展优化
(
等第:
时间
:
)7.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADC的面积为S1,△ACE的面积为S2,若S△ABC=6,则S1﹣S2的值为 .
7.5 多边形的内角和与外角和(1)
班级:___________ 姓名:____________
应知应会
1.一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺
前的∠C的度数为 ( )
A.75° B.60° C.45° D.40°
2.如图,在△ABC中,AD平分∠BAC,∠C=30°,∠DAC=45°,则∠B的度数为 °.
3.如图,∠A=∠C=90°,AD、BC交于点E,∠2=25°,则∠1的值为 °.
(
(第
4
题)
) (
(第
3
题)
) (
(第
2
题)
) (
(第
1
题)
)
4.如图,△ABC,∠B、∠C的平分线BE,CD交于点F,若∠BFC=116°,则∠A= °.
5. 已知△ABC中,∠A=30°,∠C=2∠B,则∠B= °.
巩固提升
6. 如图,在△ABC中,∠ABC=80°,∠C=70°,且BE∥AC,则∠EBD= °.
7. 如图,在△ABC中,AD是∠BAC的平分线,E为AD上一点,且EF⊥BC于点F,若∠C=35°,∠DEF=15°,则∠B的度数为 °.
(
(第
7
题)
) (
(第
6
题)
)
拓展优化
8. 如图,在△ABC中,∠ABC=56°,∠ACB=44°,AD是BC边上的高,AE是△ABC的平分线,求∠DAE的度数.
(
(第
8
题)
)
(
等第:
时间
:
)
7.5 多边形的内角和与外角和(2)
班级:___________ 姓名:____________
应知应会
1.七边形的内角和为 °.
2.如图所示,∠B的值为 °.
3.如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为 °.
4.一个多边形的每个内角均为150°,则这个多边形是 边形
(
(第
7
题)
) (
(第
5
题)
) (
(第
3
题)
) (
(第
2
题)
)
5.如图,在五边形ABCDE中,∠A+∠B+∠E=320°,DP、CP分别平分∠EDC、∠BCD,则∠CPD的度数是 °.
6.在四边形ABCD中,∠A:∠B:∠C:∠D=2:3:4:6,则∠B的度数是 °.
巩固提升
7.如图,多边形ABCDEFG中,∠E=∠F=∠G=108°,∠C=∠D=72°,则∠A+∠B的值为 °.
8.如图,五边形ABCDE的每个内角都相等,已知EF⊥BC,求证:EF平分∠AED.
(
(第
8
题)
)
拓展优化
9.如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,
将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC.
求:(1)∠F的度数;(2)∠D的度数.
(
等第:
时间
:
)
(
(第
9
题)
)
7.5 多边形的内角和与外角和(3)
班级:___________ 姓名:____________
应知应会
1.六边形的外角和为 °.
2.若n边形的内角和等于外角和的3倍,则边数n为 .
3.若一个多边形的每一个外角都等于36°,则这个多边形的内角和为 °.
4.若一个多边形的内角和与外角和总共是900°,则此多边形是 边形
5.一个多边形的边数每增加一条,这个多边形的 ( )
A.内角和增加360° B.外角和增加360° C.内角和增加180° D.对角线增加一条
巩固提升
6.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于 °.
7.如图,把△ABC纸片沿DE折叠,使点A落在图中的A'处,若∠A=25°,∠BDA'=120°,则∠A'EC= °.
(
(第
7
题)
) (
(第
6
题)
)
拓展优化
8.如图①,∠1、∠2是四边形ABCD的两个不相邻的外角.
(1)猜想并说明∠1+∠2与∠A、∠C的数量关系;
(2)如图②,在四边形ABCD中,∠ABC与∠ADC的平分线交于点O.若∠A=50°,
∠C=150°,求∠BOD的度数;
(3)如图③,BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线.请直接写出∠A、∠C与∠O的的数量关系 .
(
等第:
时间
:
)
第7章 单元测过关
(时间:60分钟 满分:150分)
班级:___________ 姓名:____________
一、选择题(每题4分,共32分)
1.把右边如图所示的海豚吉祥物进行平移,能得到的图形是 ( )
A. B. C. D.
2.用下列长度的三根木棒首尾相接,能做成三角形框架的是 ( )
A.2cm,2cm,4cm B.3cm,4cm,5cm C.1cm,2cm,3cm D.2cm,3cm,6cm
3.如图,能判断AB∥CD的条件是 ( )
A.∠A=∠DCE B.∠A=∠ACD C.∠B=∠ACB D.∠B=∠ACD
4.如图所示,AB∥CD,∠A=50°,∠C=27°,则∠AEC的大小应为 ( )
A.23° B.70° C.77° D.80°
5.如图,将一副直角三角板按照图中所示位置摆放,点E在边AB上,两条斜边互相平行,
∠DEF=∠ABC=90°,∠A=30°,∠D=45°,则∠AED等于 ( )
(
(第
3
题)
(第
4
题)
(第
5
题)
(第
7
题)
)A.15° B.20° C.25° D.30°
(
(第
8
题)
)6.列说法中错误的是 ( )
A.三角形的一个外角大于任何一个内角
B.有一个内角是直角的三角形是直角三角形
C.任意三角形的外角和都是360°
D.三角形的中线、角平分线,高线都是线段
7.如图,五边形ABCDE的一个内角∠A=110°,则∠1+∠2+∠3+∠4等于 ( )
A.360° B.290° C.270° D.250°
8.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,
GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
二、填空题(每题4分,共40分)
9.在△ABC中,∠A=36°,∠B=∠C,则∠B= °.
10.一个多边形的内角和为2700°,则这个多边形的边数是 边.
11.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为 °.
12.一架飞机向北飞行,两次改变方向后,前进的方向与原来的航行方向平行,已知第一次向
左拐50°,那么第二次向右拐 。
13. 如图,△ABC沿BC方向平移4cm得到△DEF,如果四边形ABFD的周长是32cm,则△DEF的周长是 cm.
(
(第
11
题)
(第
13
题)
(第
14
题)
)14. 如图,六边形ABCDEF的各角都相等,若m∥n,则∠1+∠2= °.
15.如图,三角形纸片ABC中∠A=66°,∠B=73°,将纸片一角折叠,使点C落在△ABC的内部C′处,若∠2=55°,则∠1= .
16.如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,
④∠D=∠ACB,正确的有结论有 个.
17.如图所示,分别以五边形ABCDE的顶点为圆心,以单位1为半径画圆,则图中阴影
(
(第
16
题)
(第
15
题)
(第
17
题)
)部分的面积之和为 平方单位.
18.定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为30°,那么这个“特征角”α的度数为 °.
三、解答题(共78分)
19.(满分8分) 如图在方格纸中,△ABC的顶点都在方格纸的格点上.
(1)将△ABC平移后得到△A′B′C′,图中已画出B点
的对应点B′,请补全△A′B′C′;
(2)画出△A′B′C′的高C′H以及中线A′D;
(3)直接写出BB′和CC′的数量关系: .
20. (满分8分)已知:如图,DE∥BC,BE平分∠ABC.已知∠1=35°.求∠3的度数.
21. (满分8分)如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,∠1=∠2,问AF与BC有怎样的位置关系?为什么?
22. (满分12分)如图,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1=48°,求∠2的度数;
(2)求证:AB∥DE.
23. (满分12分)如图,AH⊥BC于点H,点D,E分别在AB,AC上,DF⊥BC于F.
∠B=55°,∠1=35°.
(1)求证:EH∥AB.
(2)求∠2的度数.
24. (满分14分)如图,在四边形ABCD中,∠A与∠C互补,∠ABC、∠ADC的平分线分别交CD、AB于点E、F.EG∥AB,交BC于点G.
(1)∠1与∠2有怎样的数量关系?为什么?
(2)若∠A=100°,∠1=42°,求∠CEG的度数.
25.(满分16分)∠MOQ=90°,点A,B分别在射线OM、OQ上运动(不与点O重合).
(1)如图1,AI平分∠BAO,BI平分∠ABO,若∠BAO=40°,则∠AIB= °;
(2)如图2,AI平分∠BAO,BC平分∠ABM,BC的反向延长线交AI于点D.
①若∠BAO=40°,则∠ADB= °;
②点A、B在运动的过程中,∠ADB是否发生变化,若不变,试求∠ADB的度数;若变化,请说明变化规律.
(3)如图3,已知点E在BA的延长线上,∠BAO的角平分线AI、∠OAE的角平分线AF
与∠BOP的角平分线所在的直线分别相交于的点D、F,在△ADF中,如果有一个角的
度数是另一个角的4倍,请直接写出∠ABO的度数.
参考答案:
第7章 单元测过关
1.C. 2.B. 3.B. 4.C. 5.A. 6.A. 7.B. 8.C. 9. 72. 10. 17. 11. 130. 12. 50. 13. 24. 14. 180. 15. 27. 16. 3. 17. π. 18. 30°、60°或100°. 19. (1)如图,△A′B′C′即为所求;
(2)高C′H、中线A′D即为所求;(3)BB′和CC′的数量关系为:相等. 20. ∵因为DE∥BC,∴所以∠2=∠3,∵因为BE平分∠ABC,∴所以∠1=∠2,∴所以∠3=∠1=35°.21. AF与BC的位置关系是平行,理由如下:因为DE∥AC,所以∠1=∠C,因为∠1=∠2,所以∠C=∠2,所以AF∥BC. 22. (1)因为六边形ABCDEF的各内角相等,所以一个内角的大小为,所以∠E=∠F=∠BAF=120°.因为∠FAB=120°,∠1=48°,所以∠FAD=∠FAB﹣∠DAB=120°﹣48°=72°.因为∠2+∠FAD+∠F+∠E=360°,∠F=∠E=120°,所以∠ADE=360°﹣∠FAD﹣∠F﹣∠E=360°﹣72°﹣120°﹣120°=48°;(2)证明:因为∠1=120°﹣∠DAF,∠2=360°﹣120°﹣120°﹣∠DAF=120°﹣∠DAF,所以∠1=∠2,所以AB∥DE. 23. (1)因为AH⊥BC,所以∠AHC=90°,因为∠1=35°.所以∠EHC=55°,因为∠B=55°,所以∠B=∠3,所以EH∥AB(同位角相等,两直线平行).(2)因为EH∥AB,所以∠1=∠BAH=35°(两直线平行,内错角相等),因为AH⊥BC,DF⊥BC,所以AH∥DF,所以∠2+∠BAH=180°(两直线平行,同旁内角互补),所以∠2=145°. 24. (1)∠1与∠2互余.因为四边形ABCD的内角和为360°,∠A与∠C互补,所以∠ABC+∠ADC=360°﹣180°=180°,因为BE、DF分别平分∠ABC、∠ADC,所以,,因为EG∥AB,所以∠2=∠ABE,所以∠1+∠2=,即∠1与∠2互余;(2)因为∠A=100°,∠1=42°,所以∠C=80°,∠2=48°,所以∠ABE=∠CBE=48°,所以∠BEC=180°﹣48°﹣80°=52°,所以∠CEG=52°﹣48°=4°.25. (1)135°;(2)如图2中,①45;②不变,理由:因为∠D=∠CBA﹣∠BAD=∠MBA﹣∠BAO=(∠MBA﹣∠BAO)=∠AOB=×90°=45°,所以点A、B在运动的过程中,∠ADB=45°.(3)当∠ABO=45°或36°时,在△ADF中,有一个角的度数是另一个角的4倍.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
