安徽省滁州市定远县育才学校2022-2023学年八年级下学期开学考试数学试题(Word版含解析)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2022-2023学年八年级下学期开学考试数学试题(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 461.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 18:03:17 | ||
图片预览




文档简介
定远县育才学校2022-2023学年八年级下学期开学考试
数学试题
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 下列四个图形中,不是轴对称图形的为( )
A. B. C. D.
2. 如图,点,点向上平移个单位,再向右平移个单位,得到点;点向上平移个单位,再向右平移个单位,得到点;点向上平移个单位,再向右平移个单位,得到点,,按这个规律平移得到点,则点的横坐标为( )
A. B. C. D.
3. 如图,四边形的顶点坐标分别为,,,,当过点的直线将四边形分成面积相等的两部分时,直线所对应的函数表达式为( )
A. B. C. D.
4. 一个装有进水管和出水管的容器,从某时刻开始的分钟内只进水不出水,在随后的分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量单位:升与时间单位:分钟之间的部分关系如图所示.下列四种说法中正确的有( )
每分钟的进水量为升.
每分钟的进水量比每分钟的出水量多升.
当时,与之间的函数关系式为.
容器从进水开始到水全部放完的时间是分钟.
A. 个 B. 个 C. 个 D. 个
5. 如图,在中,,若沿图中虚线截去,则( )
A. B. C. D.
6. 如图,≌,点在边上,若,则的度数是( )
A. B. C. D.
7. 如图,≌,,,则的度数为( )
A. B. C. D.
8. 如图所示,已知,,再添一个条件仍不能证明≌的是( )
A. B.
C. D.
9. 如图,在中,,用直尺和圆规在边上确定一点,使点到点、点的距离相等,则符合要求的作图痕迹是( )
A. B.
C. D.
10. 如图,的面积为,平分,于,连接,则的面积为( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
11. 将直线沿轴向下平移个单位长度,点关于轴的对称点落在平移后的直线上,则的值为______.
12. 如图,点是的两条角平分线的交点,若,则的大小是______ .
13. 如图的个三角形中,均有,则经过三角形的一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是______填序号.
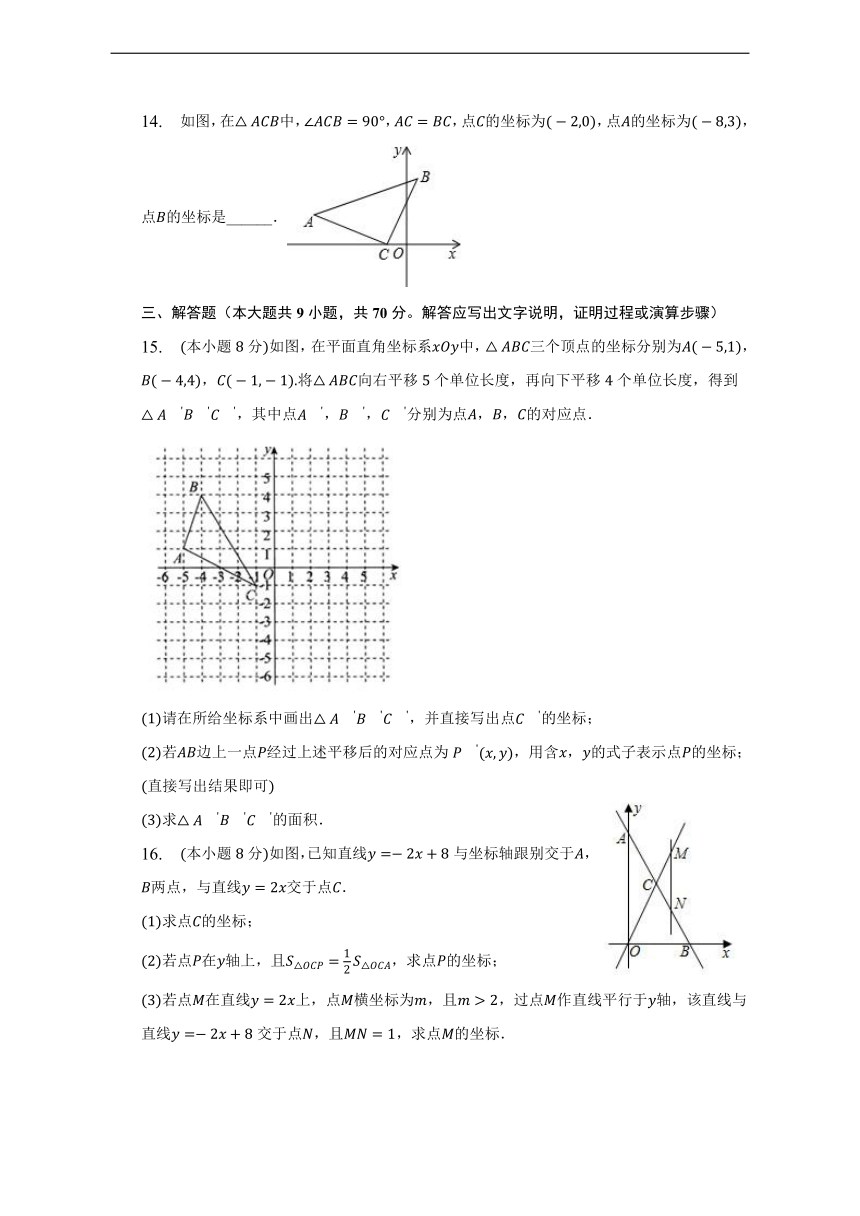
14. 如图,在中,,,点的坐标为,点的坐标为,点的坐标是______.
三、解答题(本大题共9小题,共70分。解答应写出文字说明,证明过程或演算步骤)
15. 本小题分如图,在平面直角坐标系中,三个顶点的坐标分别为,,将向右平移个单位长度,再向下平移个单位长度,得到,其中点,,分别为点,,的对应点.
请在所给坐标系中画出,并直接写出点的坐标;
若边上一点经过上述平移后的对应点为 ,用含,的式子表示点的坐标;直接写出结果即可
求的面积.
16. 本小题分如图,已知直线与坐标轴跟别交于,两点,与直线交于点.
求点的坐标;
若点在轴上,且,求点的坐标;
若点在直线上,点横坐标为,且,过点作直线平行于轴,该直线与直线交于点,且,求点的坐标.
17. 本小题分如图,在中,为边上的高,点为边上的一点,连接.
当为边上的中线时,若,的面积为,求的长;
当为的角平分线时,若,,求的度数.
18. 本小题分
某体育用品商场采购员要到厂家批发购买篮球和排球共个,篮球个数不少于排球个数,付款总额不得超过元,已知两种球厂家的批发价和商场的零售价如下表.设该商场采购个篮球.
品名 厂家批发价元个 商场零售价元个
篮球
排球
求该商场采购费用单位:元与单位:个的函数关系式,并写出自变量的取值范围;
该商场把这个球全部以零售价售出,求商场能获得的最大利润;
受原材料和工艺调整等因素影响,采购员实际采购时,篮球的批发价上调了元个,同时排球批发价下调了元个.该体育用品商场决定不调整商场零售价,发现将个球全部卖出获得的最低利润是元,求的值.
19. 本小题分
已知:,,平分,.
与全等吗?请说明理由;
若,试求与的长.
20. 本小题分已知:如图一次函数与的图象相交于点.
求点的坐标;
若一次函数与的图象与轴分别相交于点、,求的面积.
结合图象,直接写出时的取值范围.
21. 本小题分如图,在中,的垂直平分线交于点,边的垂直平分线交于点.
已知的周长,求的长;
若,,求的度数.
22. 本小题分如图所示:
若,,,求证:
若把中的题设“”与结论“”对调,所得命题是真命题吗说明理由.
23. 本小题分证明角平分线具有的性质:角平分线上的点到角的两边的距离相等.
为了更直观、清楚地表达题意,我们通常在证明之前画出图形,并用符号表示已知和求证.
如图,已知:平分,点在上,,,垂足分别为,求证:.
如图,在中,平分,交于点,于点,于点,,若,求的长.
答案和解析
1. 【解析】选项A、、能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;故选:.
2. 【解析】点的横坐标为,
点的横坐为标,
点的横坐标为,
点的横坐标为,
按这个规律平移得到点的横坐标为为,故选:.
3. 【解析】由,,,,
得,,
四边形的面积,
连接,交轴于点,可求直线的解析式为,
令,则,,,
,,
,,
要使过点的直线将四边形分成面积相等的两部分,则直线必与相交.
可求直线的解析式为,设过点的直线所对应的函数表达式为,
将点代入得,
,,
联立解得
直线与直线的交点坐标为,
直线与轴的交点坐标为,
,解得,
直线所对应的函数表达式为,故选D.
4. 【解析】由图象可得,
每分钟的进水量为,故正确;
每分钟的出水量为,故错误;
设当时,与之间的函数关系式为,把,代入得,
,
,
,故正确;
容器从进水开始到水全部放完的时间是:分钟,故正确;故选:.
5. 【解析】如图,、是的外角,
,,
即.
故选:.
6. 【解析】≌,
,,
,
,故选:.
7. 【解析】≌,,
,
.故选C.
8. 【解析】已知,,
A、添加,则,利用可以判定≌,不符合题意,
B、添加,不能判定≌,符合题意;
C、添加,利用可以判定≌,不符合题意;
D、添加,利用可以判定≌,不符合题意;故选:.
9. 【解析】要使点到点、点的距离相等,
需作的垂直平分线,
所以选项符合题意.故选:.
10. 【解析】延长交于,
平分,
,
,
,
在和中,
,
≌,
,
,,
故选:.
11.
【解析】将直线沿轴向下平移个单位长度,得直线.
点关于轴的对称点是,
把点代入,得,解得.故答案为.
12.
【解析】中,,
.
和是的角平分线,
,
在中,
,
.故答案为.
13.
【解析】过点作的角平分线,
,,
,
,,
和是等腰三角形,
正确;
不能分成两个小等腰三角形;
过点作的角平分线,
,
,,
,
和是等腰三角形;
正确;
把点分成和的角,
,,
,,
,
,
和是等腰三角形;
正确;
不能分成两个小等腰三角形.
不能分成两个小等腰三角形
故答案为:.
14.
【解析】过和分别作于,于,
,
,
,
在和中,
,
≌,
,,
点的坐标为,点的坐标为,
,,,
,,
,
则点的坐标是
故答案为.
15.如图所示:
点的坐标为;
根据将向右平移个单位长度,再向下平移个单位长度,得到,
并且边上一点经过上述平移后的对应点为 ,
点的坐标为;
的面积
.
16.由,
解得,
点的坐标为;
直线与坐标轴跟别交于,两点,
,,
,
点在轴上,且,
,
的坐标为或;
点在直线上,点横坐标为,且,
,,
,
,
,
点的坐标为
17.为边上的中线,
,
为边上的高,
,
.
,
为的角平分线,
,
,
,
,
18.根据题意得,;
,解得,
;
答:采购费用与的函数关系式为;
设总利润为,根据题意得:
,随的最大的增大,
时,元,
答:商场把这个球全部以零售价售出,能获得的最大利润为元;
由题意得:
,
当时,即时,随的增大而增大,
又,
当时,最小,
即:,
解得:舍去,
当时,即时,随的增大而减小,
又,
当时,最小,
即:,
解得:,
综上所述,将个球全部卖出获得的最低利润是元,的值为元.
19.与全等,
理由如下:平分,
,
在和中,
,
≌;
≌,
,,
,
,
,,
.
20.解方程组,得,
所以点坐标为;
当时,,,则点坐标为;
当时,,,则点坐标为;
,
的面积;
根据图象可知,时的取值范围是.
21.是线段的垂直平分线,
,
同理,,
的周长为,
,
;
,,
,,
,
,
22.证明:已知,
两直线平行,内错角相等,
已知,
等量代换,
同位角相等,两直线平行,
两直线平行,同位角相等
垂直定义;
是真命题.
理由:已知,
,
同位角相等,两直线平行,
两直线平行,同位角相等,
已知,
等量代换,
内错角相等,两直线平行.
23.证明:,,
,
平分,
,
在和中,
,
≌,
;
平分,,,
,
,
,
,
,
,
,
.
数学试题
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 下列四个图形中,不是轴对称图形的为( )
A. B. C. D.
2. 如图,点,点向上平移个单位,再向右平移个单位,得到点;点向上平移个单位,再向右平移个单位,得到点;点向上平移个单位,再向右平移个单位,得到点,,按这个规律平移得到点,则点的横坐标为( )
A. B. C. D.
3. 如图,四边形的顶点坐标分别为,,,,当过点的直线将四边形分成面积相等的两部分时,直线所对应的函数表达式为( )
A. B. C. D.
4. 一个装有进水管和出水管的容器,从某时刻开始的分钟内只进水不出水,在随后的分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量单位:升与时间单位:分钟之间的部分关系如图所示.下列四种说法中正确的有( )
每分钟的进水量为升.
每分钟的进水量比每分钟的出水量多升.
当时,与之间的函数关系式为.
容器从进水开始到水全部放完的时间是分钟.
A. 个 B. 个 C. 个 D. 个
5. 如图,在中,,若沿图中虚线截去,则( )
A. B. C. D.
6. 如图,≌,点在边上,若,则的度数是( )
A. B. C. D.
7. 如图,≌,,,则的度数为( )
A. B. C. D.
8. 如图所示,已知,,再添一个条件仍不能证明≌的是( )
A. B.
C. D.
9. 如图,在中,,用直尺和圆规在边上确定一点,使点到点、点的距离相等,则符合要求的作图痕迹是( )
A. B.
C. D.
10. 如图,的面积为,平分,于,连接,则的面积为( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
11. 将直线沿轴向下平移个单位长度,点关于轴的对称点落在平移后的直线上,则的值为______.
12. 如图,点是的两条角平分线的交点,若,则的大小是______ .
13. 如图的个三角形中,均有,则经过三角形的一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是______填序号.
14. 如图,在中,,,点的坐标为,点的坐标为,点的坐标是______.
三、解答题(本大题共9小题,共70分。解答应写出文字说明,证明过程或演算步骤)
15. 本小题分如图,在平面直角坐标系中,三个顶点的坐标分别为,,将向右平移个单位长度,再向下平移个单位长度,得到,其中点,,分别为点,,的对应点.
请在所给坐标系中画出,并直接写出点的坐标;
若边上一点经过上述平移后的对应点为 ,用含,的式子表示点的坐标;直接写出结果即可
求的面积.
16. 本小题分如图,已知直线与坐标轴跟别交于,两点,与直线交于点.
求点的坐标;
若点在轴上,且,求点的坐标;
若点在直线上,点横坐标为,且,过点作直线平行于轴,该直线与直线交于点,且,求点的坐标.
17. 本小题分如图,在中,为边上的高,点为边上的一点,连接.
当为边上的中线时,若,的面积为,求的长;
当为的角平分线时,若,,求的度数.
18. 本小题分
某体育用品商场采购员要到厂家批发购买篮球和排球共个,篮球个数不少于排球个数,付款总额不得超过元,已知两种球厂家的批发价和商场的零售价如下表.设该商场采购个篮球.
品名 厂家批发价元个 商场零售价元个
篮球
排球
求该商场采购费用单位:元与单位:个的函数关系式,并写出自变量的取值范围;
该商场把这个球全部以零售价售出,求商场能获得的最大利润;
受原材料和工艺调整等因素影响,采购员实际采购时,篮球的批发价上调了元个,同时排球批发价下调了元个.该体育用品商场决定不调整商场零售价,发现将个球全部卖出获得的最低利润是元,求的值.
19. 本小题分
已知:,,平分,.
与全等吗?请说明理由;
若,试求与的长.
20. 本小题分已知:如图一次函数与的图象相交于点.
求点的坐标;
若一次函数与的图象与轴分别相交于点、,求的面积.
结合图象,直接写出时的取值范围.
21. 本小题分如图,在中,的垂直平分线交于点,边的垂直平分线交于点.
已知的周长,求的长;
若,,求的度数.
22. 本小题分如图所示:
若,,,求证:
若把中的题设“”与结论“”对调,所得命题是真命题吗说明理由.
23. 本小题分证明角平分线具有的性质:角平分线上的点到角的两边的距离相等.
为了更直观、清楚地表达题意,我们通常在证明之前画出图形,并用符号表示已知和求证.
如图,已知:平分,点在上,,,垂足分别为,求证:.
如图,在中,平分,交于点,于点,于点,,若,求的长.
答案和解析
1. 【解析】选项A、、能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;故选:.
2. 【解析】点的横坐标为,
点的横坐为标,
点的横坐标为,
点的横坐标为,
按这个规律平移得到点的横坐标为为,故选:.
3. 【解析】由,,,,
得,,
四边形的面积,
连接,交轴于点,可求直线的解析式为,
令,则,,,
,,
,,
要使过点的直线将四边形分成面积相等的两部分,则直线必与相交.
可求直线的解析式为,设过点的直线所对应的函数表达式为,
将点代入得,
,,
联立解得
直线与直线的交点坐标为,
直线与轴的交点坐标为,
,解得,
直线所对应的函数表达式为,故选D.
4. 【解析】由图象可得,
每分钟的进水量为,故正确;
每分钟的出水量为,故错误;
设当时,与之间的函数关系式为,把,代入得,
,
,
,故正确;
容器从进水开始到水全部放完的时间是:分钟,故正确;故选:.
5. 【解析】如图,、是的外角,
,,
即.
故选:.
6. 【解析】≌,
,,
,
,故选:.
7. 【解析】≌,,
,
.故选C.
8. 【解析】已知,,
A、添加,则,利用可以判定≌,不符合题意,
B、添加,不能判定≌,符合题意;
C、添加,利用可以判定≌,不符合题意;
D、添加,利用可以判定≌,不符合题意;故选:.
9. 【解析】要使点到点、点的距离相等,
需作的垂直平分线,
所以选项符合题意.故选:.
10. 【解析】延长交于,
平分,
,
,
,
在和中,
,
≌,
,
,,
故选:.
11.
【解析】将直线沿轴向下平移个单位长度,得直线.
点关于轴的对称点是,
把点代入,得,解得.故答案为.
12.
【解析】中,,
.
和是的角平分线,
,
在中,
,
.故答案为.
13.
【解析】过点作的角平分线,
,,
,
,,
和是等腰三角形,
正确;
不能分成两个小等腰三角形;
过点作的角平分线,
,
,,
,
和是等腰三角形;
正确;
把点分成和的角,
,,
,,
,
,
和是等腰三角形;
正确;
不能分成两个小等腰三角形.
不能分成两个小等腰三角形
故答案为:.
14.
【解析】过和分别作于,于,
,
,
,
在和中,
,
≌,
,,
点的坐标为,点的坐标为,
,,,
,,
,
则点的坐标是
故答案为.
15.如图所示:
点的坐标为;
根据将向右平移个单位长度,再向下平移个单位长度,得到,
并且边上一点经过上述平移后的对应点为 ,
点的坐标为;
的面积
.
16.由,
解得,
点的坐标为;
直线与坐标轴跟别交于,两点,
,,
,
点在轴上,且,
,
的坐标为或;
点在直线上,点横坐标为,且,
,,
,
,
,
点的坐标为
17.为边上的中线,
,
为边上的高,
,
.
,
为的角平分线,
,
,
,
,
18.根据题意得,;
,解得,
;
答:采购费用与的函数关系式为;
设总利润为,根据题意得:
,随的最大的增大,
时,元,
答:商场把这个球全部以零售价售出,能获得的最大利润为元;
由题意得:
,
当时,即时,随的增大而增大,
又,
当时,最小,
即:,
解得:舍去,
当时,即时,随的增大而减小,
又,
当时,最小,
即:,
解得:,
综上所述,将个球全部卖出获得的最低利润是元,的值为元.
19.与全等,
理由如下:平分,
,
在和中,
,
≌;
≌,
,,
,
,
,,
.
20.解方程组,得,
所以点坐标为;
当时,,,则点坐标为;
当时,,,则点坐标为;
,
的面积;
根据图象可知,时的取值范围是.
21.是线段的垂直平分线,
,
同理,,
的周长为,
,
;
,,
,,
,
,
22.证明:已知,
两直线平行,内错角相等,
已知,
等量代换,
同位角相等,两直线平行,
两直线平行,同位角相等
垂直定义;
是真命题.
理由:已知,
,
同位角相等,两直线平行,
两直线平行,同位角相等,
已知,
等量代换,
内错角相等,两直线平行.
23.证明:,,
,
平分,
,
在和中,
,
≌,
;
平分,,,
,
,
,
,
,
,
,
.
同课章节目录
