安徽省滁州市定远县育才学校2022-2023学年七年级下学期开学考试数学试题(Word版含答案)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2022-2023学年七年级下学期开学考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 215.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 18:49:28 | ||
图片预览



文档简介
定远县育才学校2022-2023学年七年级下学期开学考试
数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 的相反数是( )
A. B. C. D.
2. 年月日第七次全国人口普查数据显示,安徽省人口共万人,数据万用科学记数法表示正确的是( )
A. B. C. D.
3. 下列说法正确的是( )
A. 的次数是 B. 是单项式
C. 的系数为 D. 是单项式的系数
4. 鸿星尔克某件商品的成本价为元,按成本价提高后标价,又以八折销售,这件商品的售价( )
A. 比成本价低了元 B. 比成本价低了元
C. 比成本价高了元 D. 与成本价相同
5. 今年某月的月历上圈出了相邻的三个数、、,并求出了它们的和为,这三个数在月历中的排布不可能是( )
A. B. C. D.
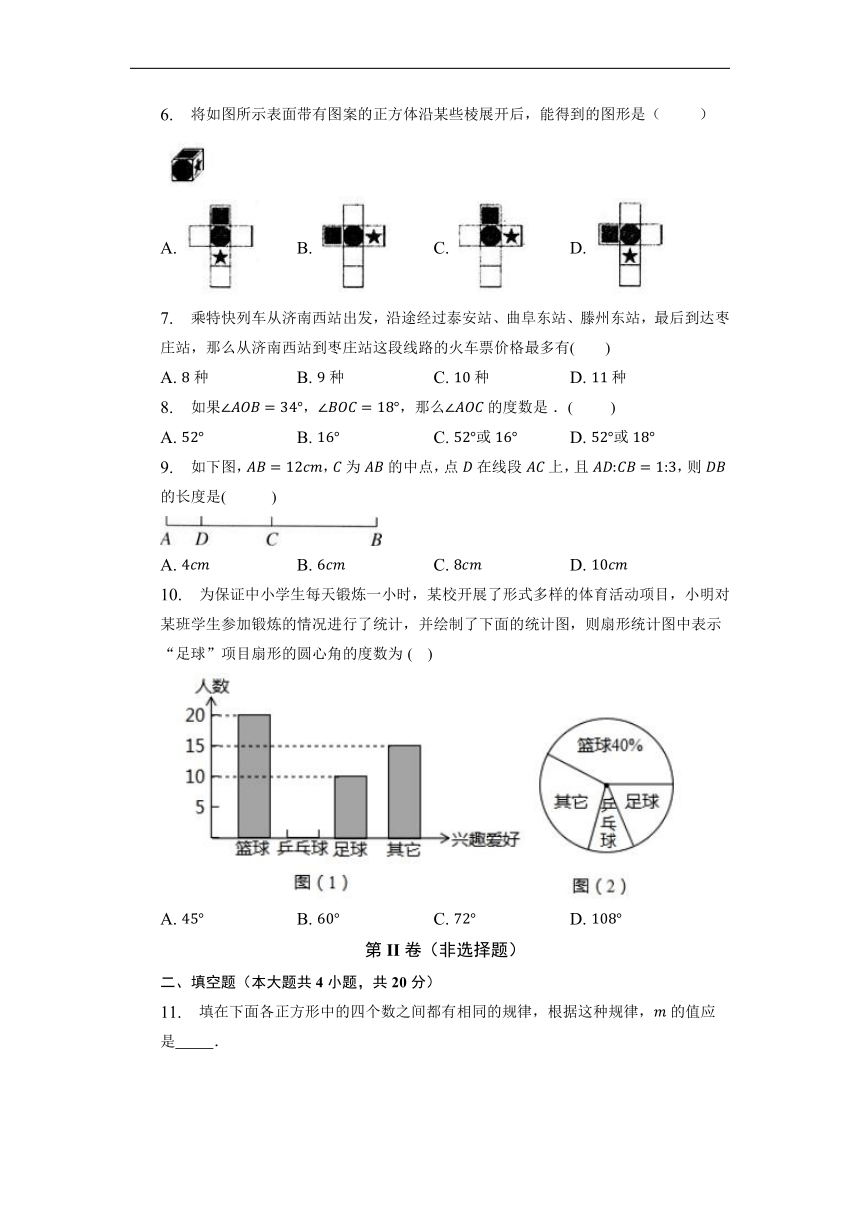
6. 将如图所示表面带有图案的正方体沿某些棱展开后,能得到的图形是( )
A. B. C. D.
7. 乘特快列车从济南西站出发,沿途经过泰安站、曲阜东站、滕州东站,最后到达枣庄站,那么从济南西站到枣庄站这段线路的火车票价格最多有( )
A. 种 B. 种 C. 种 D. 种
8. 如果,,那么的度数是.( )
A. B. C. 或 D. 或
9. 如下图,,为的中点,点在线段上,且,则的长度是( )
A. B. C. D.
10. 为保证中小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班学生参加锻炼的情况进行了统计,并绘制了下面的统计图,则扇形统计图中表示“足球”项目扇形的圆心角的度数为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共20分)
11. 填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,的值应是 .
12. 若,则代数式的值为_______.
13. 一个两位数,个位数字比十位数字大,如果把个位数字与十位数字对调,那么所得到的新数与原数的和是,原来的两位数是______.
14. ,,则______.
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题8分)解下列方程:
;
.
16. 本小题分
阅读:已知:线段如图.
求作:线段,使得线段.
小明的作法:作射线
在射线上截取.
所以线段即为所求,如图.
解决下列问题:
已知:线段如图.
请你仿照小明的作法,在图中的射线上求作点,使得不要求写作法和结论,保留作图痕迹
在的条件下,取的中点若,,求线段的长.
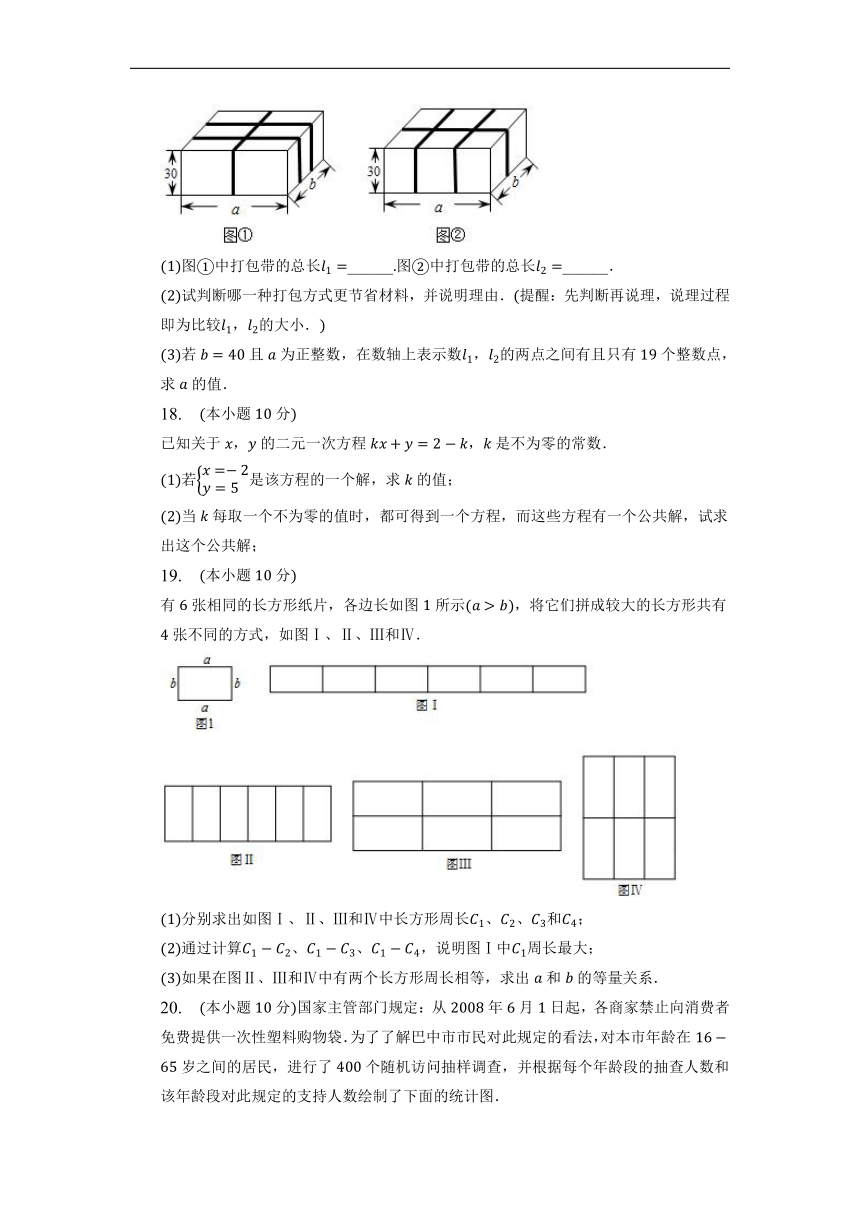
17. 本小题分火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为、、的箱子其中,准备采用如图、的两种打包方式,所用打包带的总长不计接头处的长分别记为、.
图中打包带的总长______图中打包带的总长______.
试判断哪一种打包方式更节省材料,并说明理由.提醒:先判断再说理,说理过程即为比较,的大小.
若且为正整数,在数轴上表示数,的两点之间有且只有个整数点,求的值.
18. 本小题分
已知关于,的二元一次方程,是不为零的常数.
若是该方程的一个解,求的值;
当每取一个不为零的值时,都可得到一个方程,而这些方程有一个公共解,试求出这个公共解;
19. 本小题分
有张相同的长方形纸片,各边长如图所示,将它们拼成较大的长方形共有张不同的方式,如图Ⅰ、Ⅱ、Ⅲ和Ⅳ.
分别求出如图Ⅰ、Ⅱ、Ⅲ和Ⅳ中长方形周长、、和;
通过计算、、,说明图Ⅰ中周长最大;
如果在图Ⅱ、Ⅲ和Ⅳ中有两个长方形周长相等,求出和的等量关系.
20. 本小题分国家主管部门规定:从年月日起,各商家禁止向消费者免费提供一次性塑料购物袋.为了了解巴中市市民对此规定的看法,对本市年龄在岁之间的居民,进行了个随机访问抽样调查,并根据每个年龄段的抽查人数和该年龄段对此规定的支持人数绘制了下面的统计图.
根据图提供的信息回答下列问题:
被调查的居民中,人数最多的年龄段是______ 岁.
已知被调查的人中有的人对此规定表示支持,请你求出岁年龄段的满意人数,并补全图.
比较岁和岁这两个年龄段对此规定的支持率的高低四舍五入到,注:某年龄段的支持率.
21. 本小题分今夏,某村小麦喜获丰收某种植户共收获小麦吨,现计划租用甲、乙两种货车将小麦全部运往外地销售,两辆甲种货车和一辆乙种货车可装小麦吨,一辆甲种货车和两辆乙种货车可装小麦吨.
一辆甲种货车和一辆乙种货车一次共运货多少吨?
若甲种货车每辆要付运输费元,乙种货车每辆要付运输费元,这位种植户想同时租用这两种货车,一次运完所有小麦,要求租用的每辆车都需要装满,则应如何选择方案,使运输费最少?最少运费是多少?
22. 本小题分
【概念学习】
规定:求若干个相同的有理数均不等于的除法运算叫做除方,如,等,类比有理数的乘方,我们把记作,读作“的次商”,记作,读作“的次商”一般地,我们把个相除记作,读作“的次商”.
【初步探究】
直接写出结果:______;
关于除方,下列说法错误的是______;
任何非零数的次商都等于;对于任何正整数,;;负数的奇数次商结果是负数,负数的偶数次商结果是正数.
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算能够转化为乘法运算,那么有理数的除方运算如何转化为乘方运算呢?例:.
试一试:仿照上面的算式,将下列运算结果直接写成乘方幂的形式______;______;
想一想:将一个非零有理数的次商写成幂的形式等于______;
算一算:______.
23. 本小题分
以直线上一点为端点作射线使,将一个直角三角形的直角顶点放在处注:.
如图,若直角三角板的一边放在射线上,则______;
如图,将直角三角板绕点逆时针方向转动到某个位置,若恰好平分,则______;
如图,将三角板绕点逆时针转动到某个位置时,若恰好,求的度数.
答案和解析
1. 【解析】的相反数是,故选:.
2. 【解析】万.故选:.
3. 【解析】、的次数是,此选项错误;
B、是单项式,此选项正确;
C、的系数为,此选项错误;
D、是多项式,此选项错误;故选:.
4.
【解析】该商品的售价为:元,
元,
则比成本价低了元,故选:.
5. 【解析】设最小的数是,则,解得,本选项正确,
B.设最小的数是,则,解得,本选项正确,
C.设最小的数是,则,解得,本选项错误,
D.设最小的数是,则,解得,本选项正确.故选C.
6. 【解析】根据立体图形可知五角星图案与正方形图案应是相邻面,而展开图中成了相对面,故A错误;
.根据立体图形可知五角星图案与正方形图案应是相邻面,而展开图中成了相对面,故B错误;
正方形的展开图是图,故C正确;
当将展开图折成立体图时,当正方形在上面,圆在正前面,五角星在左边,故D错误.故选C.
7. 【解析】根据题意得:从济南西站到枣庄站这段线路的火车票价格最多有:种
故选C.
8.
【解析】分为两种情况:如图,
;
如图,
,故选:.
9. 【解析】,为的中点,
,
::,
,
,
,故选:.
10. 【解析】总人数是:人,
,
则扇形统计图中表示“足球”项目扇形的圆心角度数为.故选C.
11.
【解析】根据排列规律,下面的数是,右面的数是,
因为,,,
所以,故答案为:.
12.
【解析】,
,
原式
,故答案为.
13.
【解析】设个位数字为,十位数字为,
由题意,得,
解得:,
即原来的两位数是.故答案为:.
14.
【解析】解:,,
,故答案为:.
15.解:去括号得:,
移项得:,
合并得:,
系数化为得:;
去分母得:,
去括号得:,
移项得:,
合并得:,系数化为得:.
16. 【解析】 如图所示:
因为为线段的中点,所以.
如图,点在线段的延长线上.
因为,,所以.
所以所以.
如图,点在线段上.
因为,,所以.
所以所以.
综上所述,的长为或.
17.解:图中打包带的长有长方体的个长、个宽、个高,
;
图中打包带的长有长方体的个长、个宽、个高,
;
故答案为:,;
第种打包方式更节省材料,
理由:,
,
,
,
第种打包方式更节省材料;
在数轴上表示数,的两点之间有且只有个整数点,
,
,
,
.
18.解:把代入方程,得,
解得:.
任取两个的值,不妨取,,得到两个方程并组成方程组.
解得.
即这个公共解是.
19.解:根据题意得:
,
,,,
,
,,即,
,
,
同理得:,,即最大;
,
,
,即,
当时,,即;
当时,,即.
20.解:由扇形统计图可得,
人数最多的年龄段是岁,
故答案为:;
由题意和图象可得,
岁年龄段的满意人数为:,
补全的条形统计图,如下图所示,
由题意可得,
岁这个年龄段的支持率是:,
岁这个年龄段的支持率是:,
,
岁这个年龄段的支持率高.
21.解:设一辆甲种货车可运货吨,一辆乙种货车可运货吨,
由题意得:,
解得.
.
故一辆甲种货车和一辆乙种货车一次共运货吨;
设需要甲种货车辆,乙种货车辆,
由题意得:,
.
,,且,为整数,
或.
当时,,所需费用.
当时,,所需费用.
选择甲种货车和乙种货车各辆费用最少,运费是元.
22.
解::;
故答案为:;
任何非零数的次商等于这个数与它本身相除,结果为,
任何非零数的次商都等于,
故正确;
对于任何正整数,当为奇数时,,当为偶数时,,
错误;
,,
.
错误;
负数的奇数次商结果是负数,负数的偶数次商结果是正数,
正确;
综上,说法错误的是:,
故答案为:;
,
,
故答案为:;;
,
将一个非零有理数的次商写成幂的形式等于.
故答案为:.
原式.
23.解:因为,
又因为,
所以,
故答案为:;
因为平分,
所以,
因为,
所以,,
所以;
故答案为:;
设,则.
因为,,,
所以,
解得,
即,
所以,
所以的度数为.
数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 的相反数是( )
A. B. C. D.
2. 年月日第七次全国人口普查数据显示,安徽省人口共万人,数据万用科学记数法表示正确的是( )
A. B. C. D.
3. 下列说法正确的是( )
A. 的次数是 B. 是单项式
C. 的系数为 D. 是单项式的系数
4. 鸿星尔克某件商品的成本价为元,按成本价提高后标价,又以八折销售,这件商品的售价( )
A. 比成本价低了元 B. 比成本价低了元
C. 比成本价高了元 D. 与成本价相同
5. 今年某月的月历上圈出了相邻的三个数、、,并求出了它们的和为,这三个数在月历中的排布不可能是( )
A. B. C. D.
6. 将如图所示表面带有图案的正方体沿某些棱展开后,能得到的图形是( )
A. B. C. D.
7. 乘特快列车从济南西站出发,沿途经过泰安站、曲阜东站、滕州东站,最后到达枣庄站,那么从济南西站到枣庄站这段线路的火车票价格最多有( )
A. 种 B. 种 C. 种 D. 种
8. 如果,,那么的度数是.( )
A. B. C. 或 D. 或
9. 如下图,,为的中点,点在线段上,且,则的长度是( )
A. B. C. D.
10. 为保证中小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班学生参加锻炼的情况进行了统计,并绘制了下面的统计图,则扇形统计图中表示“足球”项目扇形的圆心角的度数为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共20分)
11. 填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,的值应是 .
12. 若,则代数式的值为_______.
13. 一个两位数,个位数字比十位数字大,如果把个位数字与十位数字对调,那么所得到的新数与原数的和是,原来的两位数是______.
14. ,,则______.
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题8分)解下列方程:
;
.
16. 本小题分
阅读:已知:线段如图.
求作:线段,使得线段.
小明的作法:作射线
在射线上截取.
所以线段即为所求,如图.
解决下列问题:
已知:线段如图.
请你仿照小明的作法,在图中的射线上求作点,使得不要求写作法和结论,保留作图痕迹
在的条件下,取的中点若,,求线段的长.
17. 本小题分火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为、、的箱子其中,准备采用如图、的两种打包方式,所用打包带的总长不计接头处的长分别记为、.
图中打包带的总长______图中打包带的总长______.
试判断哪一种打包方式更节省材料,并说明理由.提醒:先判断再说理,说理过程即为比较,的大小.
若且为正整数,在数轴上表示数,的两点之间有且只有个整数点,求的值.
18. 本小题分
已知关于,的二元一次方程,是不为零的常数.
若是该方程的一个解,求的值;
当每取一个不为零的值时,都可得到一个方程,而这些方程有一个公共解,试求出这个公共解;
19. 本小题分
有张相同的长方形纸片,各边长如图所示,将它们拼成较大的长方形共有张不同的方式,如图Ⅰ、Ⅱ、Ⅲ和Ⅳ.
分别求出如图Ⅰ、Ⅱ、Ⅲ和Ⅳ中长方形周长、、和;
通过计算、、,说明图Ⅰ中周长最大;
如果在图Ⅱ、Ⅲ和Ⅳ中有两个长方形周长相等,求出和的等量关系.
20. 本小题分国家主管部门规定:从年月日起,各商家禁止向消费者免费提供一次性塑料购物袋.为了了解巴中市市民对此规定的看法,对本市年龄在岁之间的居民,进行了个随机访问抽样调查,并根据每个年龄段的抽查人数和该年龄段对此规定的支持人数绘制了下面的统计图.
根据图提供的信息回答下列问题:
被调查的居民中,人数最多的年龄段是______ 岁.
已知被调查的人中有的人对此规定表示支持,请你求出岁年龄段的满意人数,并补全图.
比较岁和岁这两个年龄段对此规定的支持率的高低四舍五入到,注:某年龄段的支持率.
21. 本小题分今夏,某村小麦喜获丰收某种植户共收获小麦吨,现计划租用甲、乙两种货车将小麦全部运往外地销售,两辆甲种货车和一辆乙种货车可装小麦吨,一辆甲种货车和两辆乙种货车可装小麦吨.
一辆甲种货车和一辆乙种货车一次共运货多少吨?
若甲种货车每辆要付运输费元,乙种货车每辆要付运输费元,这位种植户想同时租用这两种货车,一次运完所有小麦,要求租用的每辆车都需要装满,则应如何选择方案,使运输费最少?最少运费是多少?
22. 本小题分
【概念学习】
规定:求若干个相同的有理数均不等于的除法运算叫做除方,如,等,类比有理数的乘方,我们把记作,读作“的次商”,记作,读作“的次商”一般地,我们把个相除记作,读作“的次商”.
【初步探究】
直接写出结果:______;
关于除方,下列说法错误的是______;
任何非零数的次商都等于;对于任何正整数,;;负数的奇数次商结果是负数,负数的偶数次商结果是正数.
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算能够转化为乘法运算,那么有理数的除方运算如何转化为乘方运算呢?例:.
试一试:仿照上面的算式,将下列运算结果直接写成乘方幂的形式______;______;
想一想:将一个非零有理数的次商写成幂的形式等于______;
算一算:______.
23. 本小题分
以直线上一点为端点作射线使,将一个直角三角形的直角顶点放在处注:.
如图,若直角三角板的一边放在射线上,则______;
如图,将直角三角板绕点逆时针方向转动到某个位置,若恰好平分,则______;
如图,将三角板绕点逆时针转动到某个位置时,若恰好,求的度数.
答案和解析
1. 【解析】的相反数是,故选:.
2. 【解析】万.故选:.
3. 【解析】、的次数是,此选项错误;
B、是单项式,此选项正确;
C、的系数为,此选项错误;
D、是多项式,此选项错误;故选:.
4.
【解析】该商品的售价为:元,
元,
则比成本价低了元,故选:.
5. 【解析】设最小的数是,则,解得,本选项正确,
B.设最小的数是,则,解得,本选项正确,
C.设最小的数是,则,解得,本选项错误,
D.设最小的数是,则,解得,本选项正确.故选C.
6. 【解析】根据立体图形可知五角星图案与正方形图案应是相邻面,而展开图中成了相对面,故A错误;
.根据立体图形可知五角星图案与正方形图案应是相邻面,而展开图中成了相对面,故B错误;
正方形的展开图是图,故C正确;
当将展开图折成立体图时,当正方形在上面,圆在正前面,五角星在左边,故D错误.故选C.
7. 【解析】根据题意得:从济南西站到枣庄站这段线路的火车票价格最多有:种
故选C.
8.
【解析】分为两种情况:如图,
;
如图,
,故选:.
9. 【解析】,为的中点,
,
::,
,
,
,故选:.
10. 【解析】总人数是:人,
,
则扇形统计图中表示“足球”项目扇形的圆心角度数为.故选C.
11.
【解析】根据排列规律,下面的数是,右面的数是,
因为,,,
所以,故答案为:.
12.
【解析】,
,
原式
,故答案为.
13.
【解析】设个位数字为,十位数字为,
由题意,得,
解得:,
即原来的两位数是.故答案为:.
14.
【解析】解:,,
,故答案为:.
15.解:去括号得:,
移项得:,
合并得:,
系数化为得:;
去分母得:,
去括号得:,
移项得:,
合并得:,系数化为得:.
16. 【解析】 如图所示:
因为为线段的中点,所以.
如图,点在线段的延长线上.
因为,,所以.
所以所以.
如图,点在线段上.
因为,,所以.
所以所以.
综上所述,的长为或.
17.解:图中打包带的长有长方体的个长、个宽、个高,
;
图中打包带的长有长方体的个长、个宽、个高,
;
故答案为:,;
第种打包方式更节省材料,
理由:,
,
,
,
第种打包方式更节省材料;
在数轴上表示数,的两点之间有且只有个整数点,
,
,
,
.
18.解:把代入方程,得,
解得:.
任取两个的值,不妨取,,得到两个方程并组成方程组.
解得.
即这个公共解是.
19.解:根据题意得:
,
,,,
,
,,即,
,
,
同理得:,,即最大;
,
,
,即,
当时,,即;
当时,,即.
20.解:由扇形统计图可得,
人数最多的年龄段是岁,
故答案为:;
由题意和图象可得,
岁年龄段的满意人数为:,
补全的条形统计图,如下图所示,
由题意可得,
岁这个年龄段的支持率是:,
岁这个年龄段的支持率是:,
,
岁这个年龄段的支持率高.
21.解:设一辆甲种货车可运货吨,一辆乙种货车可运货吨,
由题意得:,
解得.
.
故一辆甲种货车和一辆乙种货车一次共运货吨;
设需要甲种货车辆,乙种货车辆,
由题意得:,
.
,,且,为整数,
或.
当时,,所需费用.
当时,,所需费用.
选择甲种货车和乙种货车各辆费用最少,运费是元.
22.
解::;
故答案为:;
任何非零数的次商等于这个数与它本身相除,结果为,
任何非零数的次商都等于,
故正确;
对于任何正整数,当为奇数时,,当为偶数时,,
错误;
,,
.
错误;
负数的奇数次商结果是负数,负数的偶数次商结果是正数,
正确;
综上,说法错误的是:,
故答案为:;
,
,
故答案为:;;
,
将一个非零有理数的次商写成幂的形式等于.
故答案为:.
原式.
23.解:因为,
又因为,
所以,
故答案为:;
因为平分,
所以,
因为,
所以,,
所以;
故答案为:;
设,则.
因为,,,
所以,
解得,
即,
所以,
所以的度数为.
同课章节目录
