2022-2023学年人教版九年级数学下册28.2.2应用举例 同步练习(无答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册28.2.2应用举例 同步练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 261.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 08:44:43 | ||
图片预览

文档简介
28.2.2应用举例
姓名: 得分: 日期:
一、选择题(本大题共 7 小题)
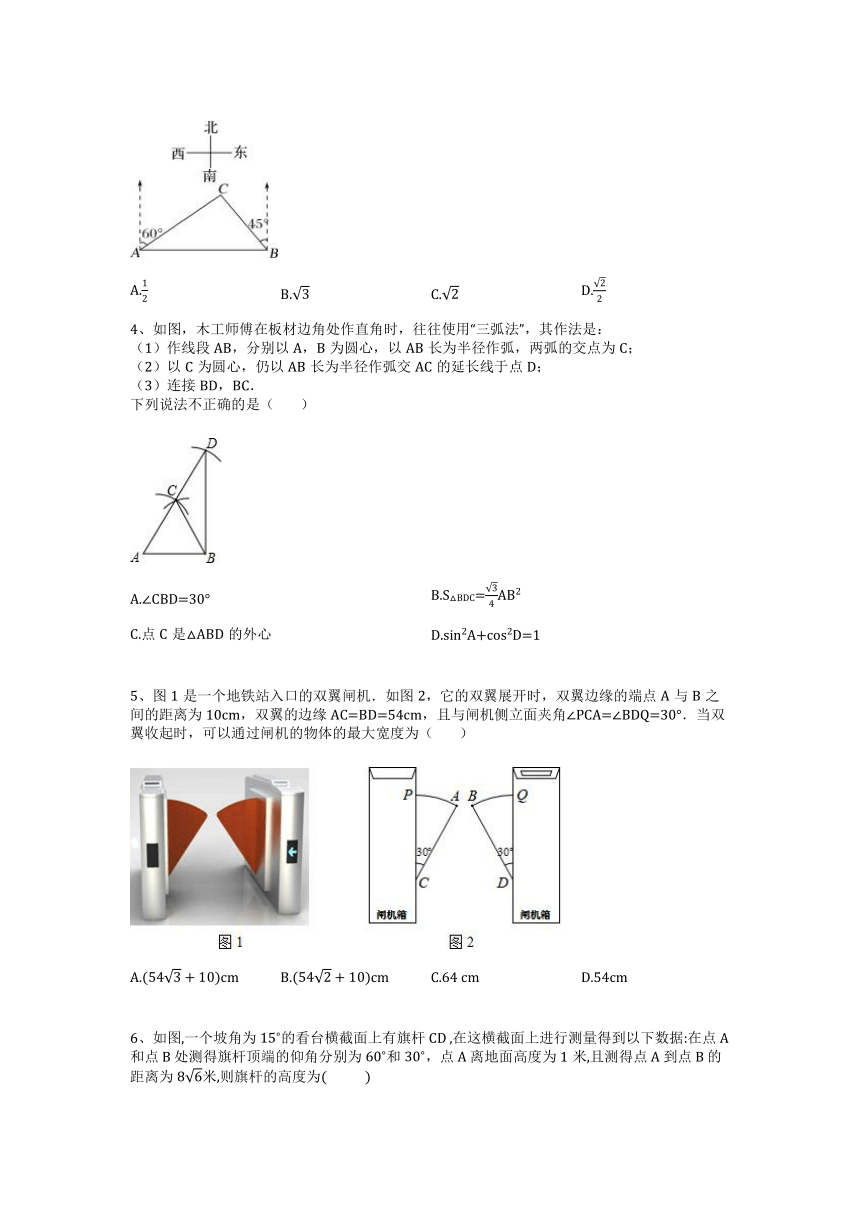
1、如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40 海里 B.40 海里 C.80海里 D.40 海里
2、如图,在斜坡EF上有一信号发射塔CD,某兴趣小组想要测量发射塔CD的高度,于是在水平地面用仪器测得塔顶D的仰角为31°,已知仪器AB高为2m,斜坡EF的坡度为i=3:4,塔底距离坡底的距离CE=10m,最后测得塔高为12m,A、B、C、D、E在同一平面内,则仪器到坡底距离AE约为( )米
(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)
A.18.6 B.18.7 C.22.0 D.24.0
3、如图,在一笔直的沿湖道路l上有A,B两个游船码头,观光岛屿C在码头A北偏东60°的方向,在码头B北偏西45°的方向,AC=8 km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A,B的游船速度分别为v1,v2,若他回到A,B所用时间相等,则 等于( )
A. B. C. D.
4、如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;
(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
下列说法不正确的是( )
A.∠CBD=30° B.S△BDC= AB2
C.点C是△ABD的外心 D.sin2A+cos2D=1
5、图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. cm B. cm C.64 cm D.54cm
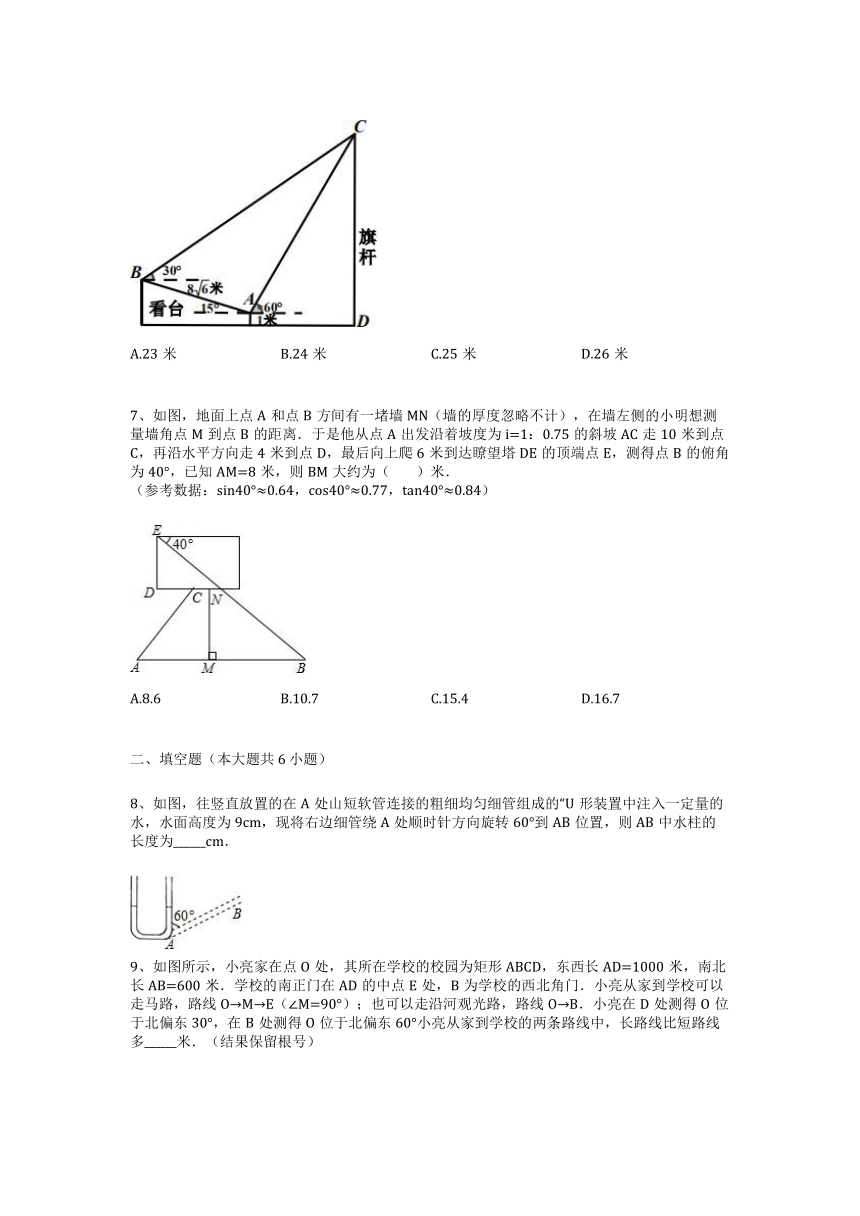
6、如图,一个坡角为 的看台横截面上有旗杆 CD ,在这横截面上进行测量得到以下数据:在点 A 和点 B 处测得旗杆顶端的仰角分别为 和 ,点 A 离地面高度为1米,且测得点 A 到点 B 的距离为 米,则旗杆的高度为( )
A.23米 B.24米 C.25米 D.26米
7、如图,地面上点A和点B方间有一堵墙MN(墙的厚度忽略不计),在墙左侧的小明想测量墙角点M到点B的距离.于是他从点A出发沿着坡度为i=1:0.75的斜坡AC走10米到点C,再沿水平方向走4米到点D,最后向上爬6米到达瞭望塔DE的顶端点E,测得点B的俯角为40°,已知AM=8米,则BM大约为( )米.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
A.8.6 B.10.7 C.15.4 D.16.7
二、填空题(本大题共 6 小题)
8、如图,往竖直放置的在A处山短软管连接的粗细均匀细管组成的“U形装置中注入一定量的水,水面高度为9cm,现将右边细管绕A处顺时针方向旋转60°到AB位置,则AB中水柱的长度为______cm.
9、如图所示,小亮家在点O处,其所在学校的校园为矩形ABCD,东西长AD=1000米,南北长AB=600米.学校的南正门在AD的中点E处,B为学校的西北角门.小亮从家到学校可以走马路,路线O→M→E(∠M=90°);也可以走沿河观光路,路线O→B.小亮在D处测得O位于北偏东30°,在B处测得O位于北偏东60°小亮从家到学校的两条路线中,长路线比短路线多______米.(结果保留根号)
10、如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.则该电线杆PQ的高度是______(结果可保留根号)
11、永定塔是北京园博园的标志性建筑,其外观为辽金风格的八角九层木塔,游客可登至塔顶,俯瞰园博园全貌.如图,在A处测得∠CAD=30°,在B处测得∠CBD=45°,并测得AB=52米,那么永定塔的高CD约是______米.( ≈1.4, ≈1.7,结果保留整数)
12、如图,已知∠MAN=30°,点B在边AM上,且AB=4 ,点P从点A出发沿射线AN方向运动,在边AN上取点C(点C在点P右侧),连结BP,BC.设PC=m,当△BPC成为等腰三角形的个数恰好有3个时,m的值为______.
13、某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)______米.
三、解答题(本大题共 6 小题)
14、某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计,EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
15、如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈ ,cos21°≈ ,tan20°≈ ,tan43°≈ ,所有结果精确到个位)
16、某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
17、夏季多雨,在山坡CD处出现了滑坡,为了测量山体滑坡的坡面长度CD,探测队在距离坡底C点 米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
18、如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端C在OP上滑动,将窗户OM按图示方向向内旋转37°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为28°,点D到点O的距离为30cm.
(1)求B点到OP的距离;
(2)求滑动支架的长.(结果精确到0.1)
(数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin 53°≈0.8,cos53°≈0.6,tan53°≈1.33)
19、如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有暗礁的危险?
姓名: 得分: 日期:
一、选择题(本大题共 7 小题)
1、如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40 海里 B.40 海里 C.80海里 D.40 海里
2、如图,在斜坡EF上有一信号发射塔CD,某兴趣小组想要测量发射塔CD的高度,于是在水平地面用仪器测得塔顶D的仰角为31°,已知仪器AB高为2m,斜坡EF的坡度为i=3:4,塔底距离坡底的距离CE=10m,最后测得塔高为12m,A、B、C、D、E在同一平面内,则仪器到坡底距离AE约为( )米
(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)
A.18.6 B.18.7 C.22.0 D.24.0
3、如图,在一笔直的沿湖道路l上有A,B两个游船码头,观光岛屿C在码头A北偏东60°的方向,在码头B北偏西45°的方向,AC=8 km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A,B的游船速度分别为v1,v2,若他回到A,B所用时间相等,则 等于( )
A. B. C. D.
4、如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;
(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
下列说法不正确的是( )
A.∠CBD=30° B.S△BDC= AB2
C.点C是△ABD的外心 D.sin2A+cos2D=1
5、图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. cm B. cm C.64 cm D.54cm
6、如图,一个坡角为 的看台横截面上有旗杆 CD ,在这横截面上进行测量得到以下数据:在点 A 和点 B 处测得旗杆顶端的仰角分别为 和 ,点 A 离地面高度为1米,且测得点 A 到点 B 的距离为 米,则旗杆的高度为( )
A.23米 B.24米 C.25米 D.26米
7、如图,地面上点A和点B方间有一堵墙MN(墙的厚度忽略不计),在墙左侧的小明想测量墙角点M到点B的距离.于是他从点A出发沿着坡度为i=1:0.75的斜坡AC走10米到点C,再沿水平方向走4米到点D,最后向上爬6米到达瞭望塔DE的顶端点E,测得点B的俯角为40°,已知AM=8米,则BM大约为( )米.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
A.8.6 B.10.7 C.15.4 D.16.7
二、填空题(本大题共 6 小题)
8、如图,往竖直放置的在A处山短软管连接的粗细均匀细管组成的“U形装置中注入一定量的水,水面高度为9cm,现将右边细管绕A处顺时针方向旋转60°到AB位置,则AB中水柱的长度为______cm.
9、如图所示,小亮家在点O处,其所在学校的校园为矩形ABCD,东西长AD=1000米,南北长AB=600米.学校的南正门在AD的中点E处,B为学校的西北角门.小亮从家到学校可以走马路,路线O→M→E(∠M=90°);也可以走沿河观光路,路线O→B.小亮在D处测得O位于北偏东30°,在B处测得O位于北偏东60°小亮从家到学校的两条路线中,长路线比短路线多______米.(结果保留根号)
10、如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.则该电线杆PQ的高度是______(结果可保留根号)
11、永定塔是北京园博园的标志性建筑,其外观为辽金风格的八角九层木塔,游客可登至塔顶,俯瞰园博园全貌.如图,在A处测得∠CAD=30°,在B处测得∠CBD=45°,并测得AB=52米,那么永定塔的高CD约是______米.( ≈1.4, ≈1.7,结果保留整数)
12、如图,已知∠MAN=30°,点B在边AM上,且AB=4 ,点P从点A出发沿射线AN方向运动,在边AN上取点C(点C在点P右侧),连结BP,BC.设PC=m,当△BPC成为等腰三角形的个数恰好有3个时,m的值为______.
13、某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)______米.
三、解答题(本大题共 6 小题)
14、某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计,EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
15、如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈ ,cos21°≈ ,tan20°≈ ,tan43°≈ ,所有结果精确到个位)
16、某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
17、夏季多雨,在山坡CD处出现了滑坡,为了测量山体滑坡的坡面长度CD,探测队在距离坡底C点 米处的E点用热气球进行数据监测,当热气球垂直升腾到B点时观察滑坡的终端C点,俯视角为60°,当热气球继续垂直升腾90米到达A点,此时探测到滑坡的始端D点,俯视角为45°,若滑坡的山体坡角∠DCH为30°,求山体滑坡的坡面长度CD的长.(计算保留根号)
18、如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端C在OP上滑动,将窗户OM按图示方向向内旋转37°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为28°,点D到点O的距离为30cm.
(1)求B点到OP的距离;
(2)求滑动支架的长.(结果精确到0.1)
(数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin 53°≈0.8,cos53°≈0.6,tan53°≈1.33)
19、如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有暗礁的危险?
