2022-2023学睥人教版九年级数学下册28.2.1解直角三角形 同步练习(无答案)
文档属性
| 名称 | 2022-2023学睥人教版九年级数学下册28.2.1解直角三角形 同步练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 08:45:55 | ||
图片预览


文档简介
28.2.1解直角三角形
姓名: 得分: 日期:
一、选择题(本大题共 7 小题)
1、如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为( )
A. B. C. D.
2、如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于 MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
A.(1,0) B.( ,0)
C.( ,0) D.(2 ,0)
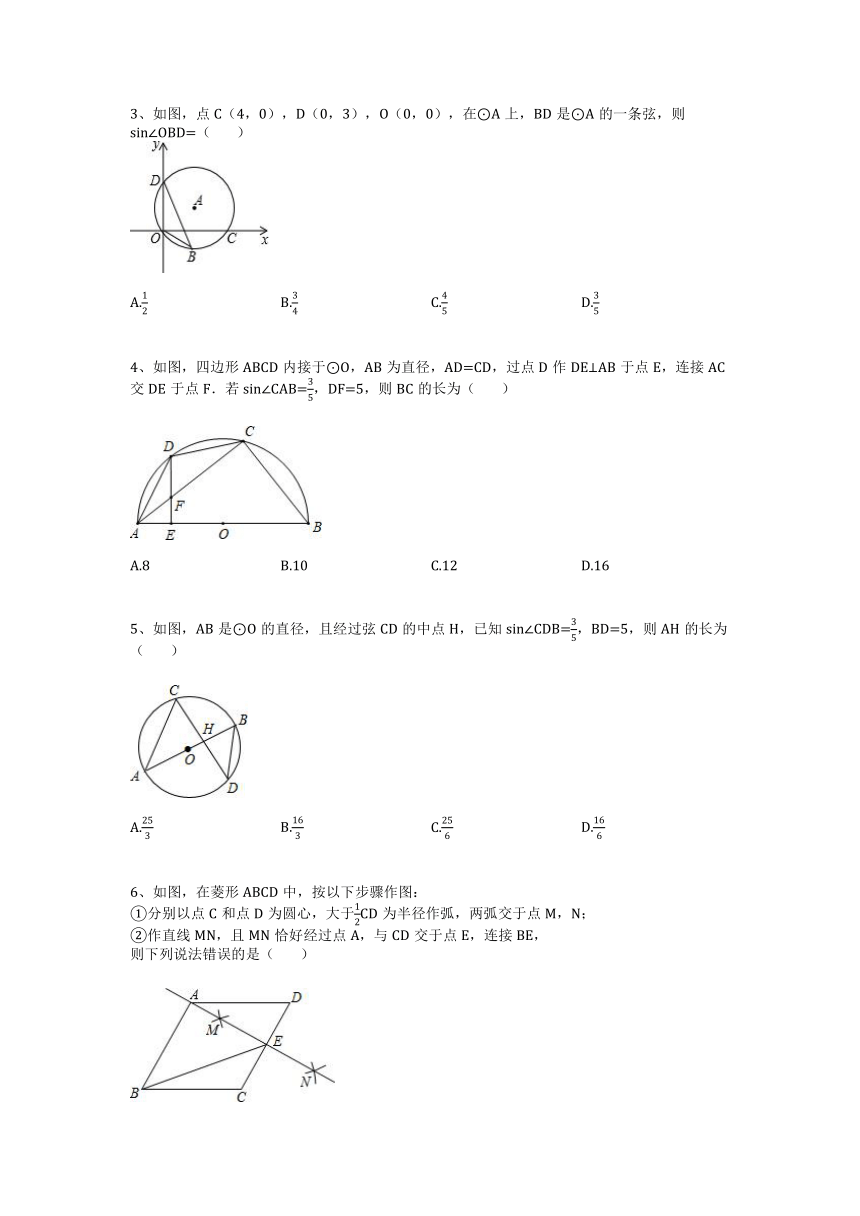
3、如图,点C(4,0),D(0,3),O(0,0),在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
4、如图,四边形ABCD内接于⊙O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F.若sin∠CAB= ,DF=5,则BC的长为( )
A.8 B.10 C.12 D.16
5、如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB= ,BD=5,则AH的长为( )
A. B. C. D.
6、如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于 CD为半径作弧,两弧交于点M,N;
②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,
则下列说法错误的是( )
A.∠ABC=60° B.S△ABE=2S△ADE
C.若AB=4,则BE= D.sin∠CBE=
7、由三角函数定义,对于任意锐角A,有sinA=cos(90°-A)及sin2A+cos2A=1成立.如图,在△ABC中,∠A,∠B是锐角,BC=a,AC=b,AB=c.CD⊥AB于D,DE∥AC交BC于E,设CD=h,BE=a',DE=b',BD=c',则下列条件中能判定△ABC是直角三角形的个数是( )
①a2+b2=c2;②aa'+bb'=cc';③sin2A+sin2B=1;④ .
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共 6 小题)
8、如图所示,在△ABD中,BC为AD边上的高线,tan∠BAD=1,在BC上截取CG=CD,连结AG,将△ACG绕点C旋转,使点G落在BD边上的F处,A落在E处,连结BE,若AD=4,tanD=3,则△CFD和△ECF的面积比为______;BE长为______.
9、如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB的值是______.
10、如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为 ,tan∠ABC= ,则CQ的最大值是______.
11、如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为______.
12、如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为______.
13、如图,边长为1的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止.第一次滚动时正方形旋转了______°,点A在滚动过程中到出发点的最大距离是______.
三、解答题(本大题共 6 小题)
14、在 中, 、b、c分别为∠A、∠B、∠C的对边.
,求b、c、 ;
(2)a+c=16,b=8,求a、c、 .
15、如图,在 中, 、∠B、∠C的对边分别为a、b、c,且 的平分线 解直角三角形ABC.
16、如图,已知⊙O的半径为2,弦AB的长为 ,点C与点D分别是劣弧AB与优弧ADB上的任一点(点C、D均不与A、B重合).
(1)求∠ACB;
(2)求 的最大面积.
17、如图,在正方形ABCD中,边长AB=3,点E(与B,C不重合)是BC边上任意一点,把EA绕点E顺时针方向旋转 到EF,连接CF.
(1)求证:CF是正方形ABCD的外角平分线;
(2)当 时,求CF的长.
18、已知:如图, 中, 为AB边上一点,PD⊥BC于D.
(1)当BP:PA=2:1时,求 、 、 ;
(2)当BP:PA=1:2时,求 、 、 .
19、将 绕点B逆时针旋转α得到 的延长线与AC相交于点F,连接DA、BF.
(1)如图1,若 .
①求证: ;②猜想线段DF、AF的数量关系,并证明你的猜想;
(2)如图2,若∠ABC < α,BF=mAF(m为常数),求 的值(用含m、α的式子表示).
姓名: 得分: 日期:
一、选择题(本大题共 7 小题)
1、如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为( )
A. B. C. D.
2、如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于 MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
A.(1,0) B.( ,0)
C.( ,0) D.(2 ,0)
3、如图,点C(4,0),D(0,3),O(0,0),在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
4、如图,四边形ABCD内接于⊙O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F.若sin∠CAB= ,DF=5,则BC的长为( )
A.8 B.10 C.12 D.16
5、如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB= ,BD=5,则AH的长为( )
A. B. C. D.
6、如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于 CD为半径作弧,两弧交于点M,N;
②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,
则下列说法错误的是( )
A.∠ABC=60° B.S△ABE=2S△ADE
C.若AB=4,则BE= D.sin∠CBE=
7、由三角函数定义,对于任意锐角A,有sinA=cos(90°-A)及sin2A+cos2A=1成立.如图,在△ABC中,∠A,∠B是锐角,BC=a,AC=b,AB=c.CD⊥AB于D,DE∥AC交BC于E,设CD=h,BE=a',DE=b',BD=c',则下列条件中能判定△ABC是直角三角形的个数是( )
①a2+b2=c2;②aa'+bb'=cc';③sin2A+sin2B=1;④ .
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共 6 小题)
8、如图所示,在△ABD中,BC为AD边上的高线,tan∠BAD=1,在BC上截取CG=CD,连结AG,将△ACG绕点C旋转,使点G落在BD边上的F处,A落在E处,连结BE,若AD=4,tanD=3,则△CFD和△ECF的面积比为______;BE长为______.
9、如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB的值是______.
10、如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为 ,tan∠ABC= ,则CQ的最大值是______.
11、如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为______.
12、如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为______.
13、如图,边长为1的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止.第一次滚动时正方形旋转了______°,点A在滚动过程中到出发点的最大距离是______.
三、解答题(本大题共 6 小题)
14、在 中, 、b、c分别为∠A、∠B、∠C的对边.
,求b、c、 ;
(2)a+c=16,b=8,求a、c、 .
15、如图,在 中, 、∠B、∠C的对边分别为a、b、c,且 的平分线 解直角三角形ABC.
16、如图,已知⊙O的半径为2,弦AB的长为 ,点C与点D分别是劣弧AB与优弧ADB上的任一点(点C、D均不与A、B重合).
(1)求∠ACB;
(2)求 的最大面积.
17、如图,在正方形ABCD中,边长AB=3,点E(与B,C不重合)是BC边上任意一点,把EA绕点E顺时针方向旋转 到EF,连接CF.
(1)求证:CF是正方形ABCD的外角平分线;
(2)当 时,求CF的长.
18、已知:如图, 中, 为AB边上一点,PD⊥BC于D.
(1)当BP:PA=2:1时,求 、 、 ;
(2)当BP:PA=1:2时,求 、 、 .
19、将 绕点B逆时针旋转α得到 的延长线与AC相交于点F,连接DA、BF.
(1)如图1,若 .
①求证: ;②猜想线段DF、AF的数量关系,并证明你的猜想;
(2)如图2,若∠ABC < α,BF=mAF(m为常数),求 的值(用含m、α的式子表示).
