1.3.2 同底数幂的除法(第2课时) 课件(共23张PPT)
文档属性
| 名称 | 1.3.2 同底数幂的除法(第2课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 20:10:18 | ||
图片预览








文档简介
(共23张PPT)
1.3.2同底数幂的除法(第2课时)
第一章
整式的乘除
北师大版七年级下册
学习目标
1.会用科学记数法表示绝对值小于1的数,能将用科学记数法表示的数还原为原数.
2.会用科学记数法解决相应的实际问题.
3.借助自己熟悉的事物感受绝对值较小的数据,体会估测微小事物的方法与策略.
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,n是正整数.
例如,864000可以写成 .
8.64×105
情境导入
情境导入
生活中,常用的长度单位有哪一些?
情境导入
“2019-nCoV”病毒是一种新型冠状病毒,它的直径大约是0.00000012m,可以通过飞沫和密切接触传播. 这种病毒不耐高温,56℃的环境中30分钟就可以灭活,常见的含氯消毒液和75%的酒精都可以对其灭火,据测算一滴稀释后某浓度的含氯消毒液可以杀死约105个冠状病毒.
戴口罩 不聚集 勤洗手 多锻炼 爱学习 常通风
探究新知
核心知识点一:
用科学计数法表示绝对值小于1的数
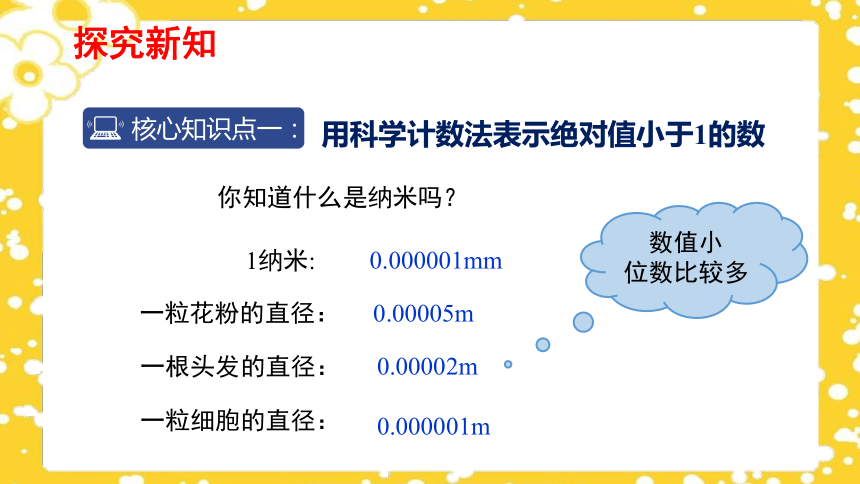
你知道什么是纳米吗?
1纳米:
一粒花粉的直径:
一根头发的直径:
一粒细胞的直径:
0.00005m
0.00002m
0.000001mm
数值小
位数比较多
0.000001m
1纳米= 0.000 000 001米
这个结果还能用科学记数法表示吗?
思考:怎样把0.000 000 001用科学记数法表示?
0.000 000 001
=1×10-9
探究新知
10-3
10-6
10-9
=0.001
=0.000001
=0.000000001
1×10-3
1×10-6
1×10-9
0.001=
0.000001=
0.000000001=
0.000091=9.1×0.00001=9.1×10-5
0.00006=6×0.00001=6×10-5
0.00000012=1.2×0.0000001=1.2×10-7
探究新知
归纳总结
表示小于1的正数科学记数法.
一般地,一个小于1的正数可以表示成a×10n,其中1≤a<10,n为负整数.
a=8.61
0.000 861=
.
0.000 861=
8.61×10-4
8.61×10-4
n个0
0.00…01
注:a满足1≤a<10
n:(1)小数点移动位数
(2)数0法(左起第一个非零数前的0的个数)
探究新知
例1 用科学记数法表示下列各数:
(1)0.000 04;(2)0.034;(3)0.000 000 45.
解:(1)0.000 04=4×10-5;
(2)0.034=3.4×10-2;
(3)0.000 000 45=4.5×10-7.
分析:数清每个数中左起第一个非0的数字前面有几个0,用科学记数法表示时10的指数就是负几.
例题讲解
例2:纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓球上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个1nm3的物体(物体之间隙忽略不计)?
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
例题讲解
例3 把下列用科学记数法表示的数还原:
(1)7.2×10-5;(2)1.5×10-4.
分析:(1)n=-5,还原后的数中7前面有5个0(包括最后整数部分的那个0);
(2)n=-4,还原后的数中1 前面有4个0(包括最后整数部分的那个0).
解:(1)7.2×10-5=0.000 072;
(2)1.5×10-4=0.000 15.
例题讲解
探究新知
5.35 ×104
8.61×10-4
同:都是a ×10n的形式,1≤ a <10
异
原数大于10
原数小于1的正数
n为正整数
n为负整数
53500=
0.000 861=
总结:科学记数法既可以表示较大的数,也可以表示较小的数.
归纳总结
探究新知
读一读
纳米(nm)是一种长度单位. 1 nm 为十亿分之一米,即 10 – 9 m,它相当于 1 根头发丝直径的六万分之一.直径为 1 nm 的球与乒乓球相比, 相当于乒乓球与地球相比.
纳米技术是指在 0.1 ~ 100 nm 范围内,通过直接操纵和安排原子、分子来创造新物质,它将对人类的未来产生深远影响.例如,采用纳米技术,可以在一块方糖大小的磁盘上存放一个国家图书馆的所有信息;应用纳米技术还可以制造出“纳米医生”,它微小到可以注入人体的血管中.
纳 米
随堂练习
1. 数据 0.000 031 4 用科学记数法表示为( )
A. 31.4×10 – 4 B. 3.14×10 – 5
C. 3.14×10 – 6 D. 0.314×10 – 6
B
2. 已知空气的单位体积质量为 1.24×10 – 3 克/厘米3,1.24×10 – 3 用小数表示为( )
A. 0.000 124 B. 0.012 4
C. – 0.001 24 D. 0.001 24
D
3. 肥皂泡的泡壁厚度大约是0.000 7 mm,0.000 7用科学记数法表示为( )
A.0.7×10-3 B.7×10-3
C.7×10-4 D.7×10-5
C
4. 将6.18×10-3化为小数是( )
A.0.000618 B.0.00618
C.0.0618 D.0.618
B
随堂练习
5.中国抗疫取得了巨大成就,堪称奇迹,为世界各国防控疫情提供了重要借鉴和支持,让中国人民倍感自豪.2020年1月12日,世界卫生组织正式将2019新型冠状病毒命名为2019-nCoV.该病毒的直径在0.000 000 08米~0.000 000 12米,将0.000 000 12用科学记数法表示为a×10n的形式,则n为( )
A.-8 B.-7 C.7 D.8
B
随堂练习
6.某颗粒物的直径是0.0000025米,把0.0000025用科学记数法表示为 .
7.据测算,5万粒芝麻的质量约为200 g,那么一粒芝麻的质量约为 g.(用科学记数法表示)
2.5× 10-6
4× 10-3
随堂练习
8.用科学记数法表示下列各数
(1)0.000 72=____________
(2)0.000 000 306 = ____________
(3)0.000 000 001 295 =____________
(1)2.1×10-4 =____________
(2)7.08×10-3=____________
(3)2.17×10-1=____________
9.把下列科学记数法表示的数还原成小数
7.2×10-4
3.06×10-7
1.295×10-9
0.0001
0.007 08
0.217
=0.000 21
2.1×
随堂练习
10.用科学记数法表示下列各数:
0.000 000 72;
0.000 861;
0.000 000 000 342 5
解:(1)0.000 000 72=7.2×10-7.
(2)0.000 861=8.61×10-4.
(3)0.000 000 000 342 5=3.425×10-10.
随堂练习
10. 用科学记数法表示下列各数:
(1)0.002 1; (2)0.000 1;
(3)0.000 305; (4)– 0.000 000 08.
2.1×10 – 3
1×10 – 4
3.05×10 – 4
– 8×10 – 8
随堂练习
11.用小数表示下列各数:
(1)2×10-7;(2)3.14×10-5;
(3)7.08×10-3;(4)2.17×10-1.
解:(1)2×10-7=0.0000002;
(2)3.14×10-5=0.0000314;
(3)7.08×10-3=0.00708;
(4)2.17×10-1=0.217.
随堂练习
课堂小结
用科学记数法表示数分为两种:
(1)当N>1时,N=a×10n,其中1≤a<10,
n=N的整数位数减1;
(2)当0n=N中第一个非零数字前0的个数.
(包括整数位上的0)
1.3.2同底数幂的除法(第2课时)
第一章
整式的乘除
北师大版七年级下册
学习目标
1.会用科学记数法表示绝对值小于1的数,能将用科学记数法表示的数还原为原数.
2.会用科学记数法解决相应的实际问题.
3.借助自己熟悉的事物感受绝对值较小的数据,体会估测微小事物的方法与策略.
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,n是正整数.
例如,864000可以写成 .
8.64×105
情境导入
情境导入
生活中,常用的长度单位有哪一些?
情境导入
“2019-nCoV”病毒是一种新型冠状病毒,它的直径大约是0.00000012m,可以通过飞沫和密切接触传播. 这种病毒不耐高温,56℃的环境中30分钟就可以灭活,常见的含氯消毒液和75%的酒精都可以对其灭火,据测算一滴稀释后某浓度的含氯消毒液可以杀死约105个冠状病毒.
戴口罩 不聚集 勤洗手 多锻炼 爱学习 常通风
探究新知
核心知识点一:
用科学计数法表示绝对值小于1的数
你知道什么是纳米吗?
1纳米:
一粒花粉的直径:
一根头发的直径:
一粒细胞的直径:
0.00005m
0.00002m
0.000001mm
数值小
位数比较多
0.000001m
1纳米= 0.000 000 001米
这个结果还能用科学记数法表示吗?
思考:怎样把0.000 000 001用科学记数法表示?
0.000 000 001
=1×10-9
探究新知
10-3
10-6
10-9
=0.001
=0.000001
=0.000000001
1×10-3
1×10-6
1×10-9
0.001=
0.000001=
0.000000001=
0.000091=9.1×0.00001=9.1×10-5
0.00006=6×0.00001=6×10-5
0.00000012=1.2×0.0000001=1.2×10-7
探究新知
归纳总结
表示小于1的正数科学记数法.
一般地,一个小于1的正数可以表示成a×10n,其中1≤a<10,n为负整数.
a=8.61
0.000 861=
.
0.000 861=
8.61×10-4
8.61×10-4
n个0
0.00…01
注:a满足1≤a<10
n:(1)小数点移动位数
(2)数0法(左起第一个非零数前的0的个数)
探究新知
例1 用科学记数法表示下列各数:
(1)0.000 04;(2)0.034;(3)0.000 000 45.
解:(1)0.000 04=4×10-5;
(2)0.034=3.4×10-2;
(3)0.000 000 45=4.5×10-7.
分析:数清每个数中左起第一个非0的数字前面有几个0,用科学记数法表示时10的指数就是负几.
例题讲解
例2:纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓球上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个1nm3的物体(物体之间隙忽略不计)?
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
例题讲解
例3 把下列用科学记数法表示的数还原:
(1)7.2×10-5;(2)1.5×10-4.
分析:(1)n=-5,还原后的数中7前面有5个0(包括最后整数部分的那个0);
(2)n=-4,还原后的数中1 前面有4个0(包括最后整数部分的那个0).
解:(1)7.2×10-5=0.000 072;
(2)1.5×10-4=0.000 15.
例题讲解
探究新知
5.35 ×104
8.61×10-4
同:都是a ×10n的形式,1≤ a <10
异
原数大于10
原数小于1的正数
n为正整数
n为负整数
53500=
0.000 861=
总结:科学记数法既可以表示较大的数,也可以表示较小的数.
归纳总结
探究新知
读一读
纳米(nm)是一种长度单位. 1 nm 为十亿分之一米,即 10 – 9 m,它相当于 1 根头发丝直径的六万分之一.直径为 1 nm 的球与乒乓球相比, 相当于乒乓球与地球相比.
纳米技术是指在 0.1 ~ 100 nm 范围内,通过直接操纵和安排原子、分子来创造新物质,它将对人类的未来产生深远影响.例如,采用纳米技术,可以在一块方糖大小的磁盘上存放一个国家图书馆的所有信息;应用纳米技术还可以制造出“纳米医生”,它微小到可以注入人体的血管中.
纳 米
随堂练习
1. 数据 0.000 031 4 用科学记数法表示为( )
A. 31.4×10 – 4 B. 3.14×10 – 5
C. 3.14×10 – 6 D. 0.314×10 – 6
B
2. 已知空气的单位体积质量为 1.24×10 – 3 克/厘米3,1.24×10 – 3 用小数表示为( )
A. 0.000 124 B. 0.012 4
C. – 0.001 24 D. 0.001 24
D
3. 肥皂泡的泡壁厚度大约是0.000 7 mm,0.000 7用科学记数法表示为( )
A.0.7×10-3 B.7×10-3
C.7×10-4 D.7×10-5
C
4. 将6.18×10-3化为小数是( )
A.0.000618 B.0.00618
C.0.0618 D.0.618
B
随堂练习
5.中国抗疫取得了巨大成就,堪称奇迹,为世界各国防控疫情提供了重要借鉴和支持,让中国人民倍感自豪.2020年1月12日,世界卫生组织正式将2019新型冠状病毒命名为2019-nCoV.该病毒的直径在0.000 000 08米~0.000 000 12米,将0.000 000 12用科学记数法表示为a×10n的形式,则n为( )
A.-8 B.-7 C.7 D.8
B
随堂练习
6.某颗粒物的直径是0.0000025米,把0.0000025用科学记数法表示为 .
7.据测算,5万粒芝麻的质量约为200 g,那么一粒芝麻的质量约为 g.(用科学记数法表示)
2.5× 10-6
4× 10-3
随堂练习
8.用科学记数法表示下列各数
(1)0.000 72=____________
(2)0.000 000 306 = ____________
(3)0.000 000 001 295 =____________
(1)2.1×10-4 =____________
(2)7.08×10-3=____________
(3)2.17×10-1=____________
9.把下列科学记数法表示的数还原成小数
7.2×10-4
3.06×10-7
1.295×10-9
0.0001
0.007 08
0.217
=0.000 21
2.1×
随堂练习
10.用科学记数法表示下列各数:
0.000 000 72;
0.000 861;
0.000 000 000 342 5
解:(1)0.000 000 72=7.2×10-7.
(2)0.000 861=8.61×10-4.
(3)0.000 000 000 342 5=3.425×10-10.
随堂练习
10. 用科学记数法表示下列各数:
(1)0.002 1; (2)0.000 1;
(3)0.000 305; (4)– 0.000 000 08.
2.1×10 – 3
1×10 – 4
3.05×10 – 4
– 8×10 – 8
随堂练习
11.用小数表示下列各数:
(1)2×10-7;(2)3.14×10-5;
(3)7.08×10-3;(4)2.17×10-1.
解:(1)2×10-7=0.0000002;
(2)3.14×10-5=0.0000314;
(3)7.08×10-3=0.00708;
(4)2.17×10-1=0.217.
随堂练习
课堂小结
用科学记数法表示数分为两种:
(1)当N>1时,N=a×10n,其中1≤a<10,
n=N的整数位数减1;
(2)当0
(包括整数位上的0)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
