17.1勾股定理(3) 课件(共22张PPT)
文档属性
| 名称 | 17.1勾股定理(3) 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 21:14:35 | ||
图片预览





文档简介
(共22张PPT)
17.1勾股定理(3)
人教版八年级下册
教学目标
2. 能利用勾股定理在数轴上作出表示无理数的点.
1. 会用勾股定理解决简单的实际问题,建立数形结合的思想.
3.灵活运用勾股定理进行计算,并会运用勾股定理解决相应的折叠问题.
新知导入
欣赏下面海螺的图片:
在数学中也有这样一幅美丽的“海螺型”图案,
如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?
新知讲解
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
知识点 1
证明“HL”
已知:如图,在Rt△ABC 和Rt△A′B′ C′中,
∠C=∠C′=90°,AB=A′B ′,AC=A′C′ .
求证:△ABC≌△ A′B′ C′ .
新知讲解
′
′
′
′
′
′
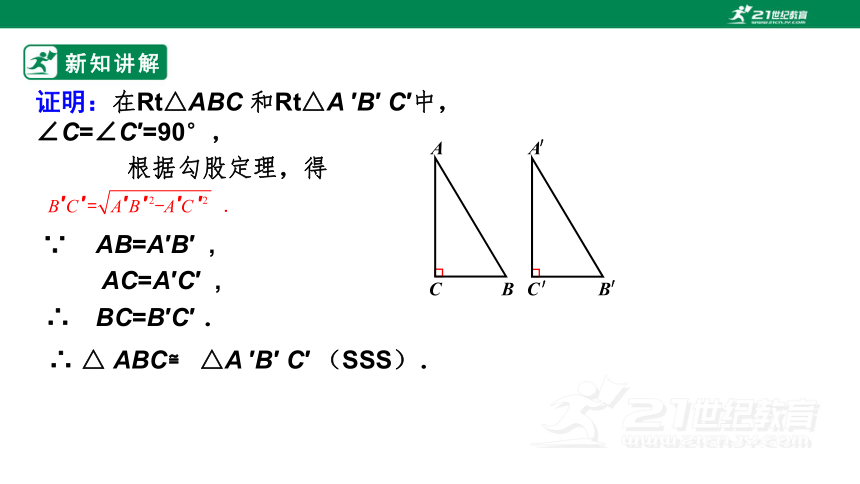
证明:在Rt△ABC 和Rt△A ′B′ C′中,∠C=∠C′=90°,
根据勾股定理,得
A
B
C
A
B
C′
′
′
∵ AB=A′B′ ,
AC=A′C′ ,
∴ BC=B′C′ .
∴ △ ABC≌ △A ′B′ C′ (SSS).
新知讲解
-1 0 1 2 3
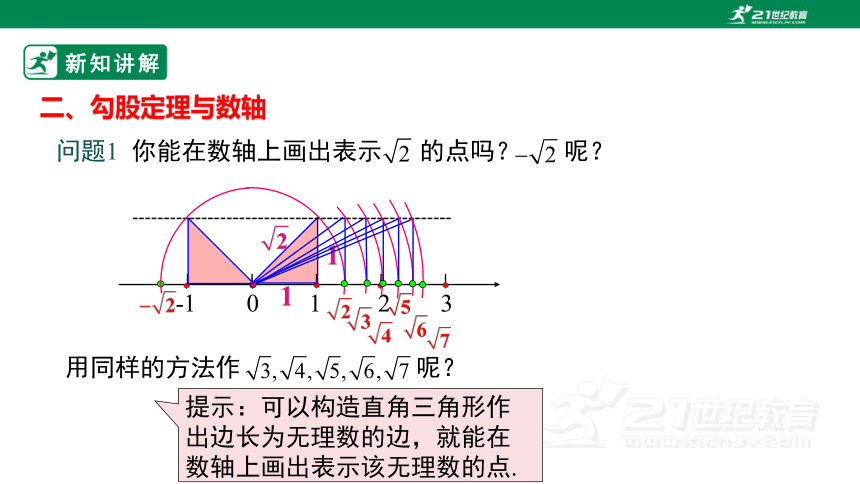
问题1 你能在数轴上画出表示 的点吗? 呢?
用同样的方法作 呢?
二、勾股定理与数轴
提示:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
新知讲解
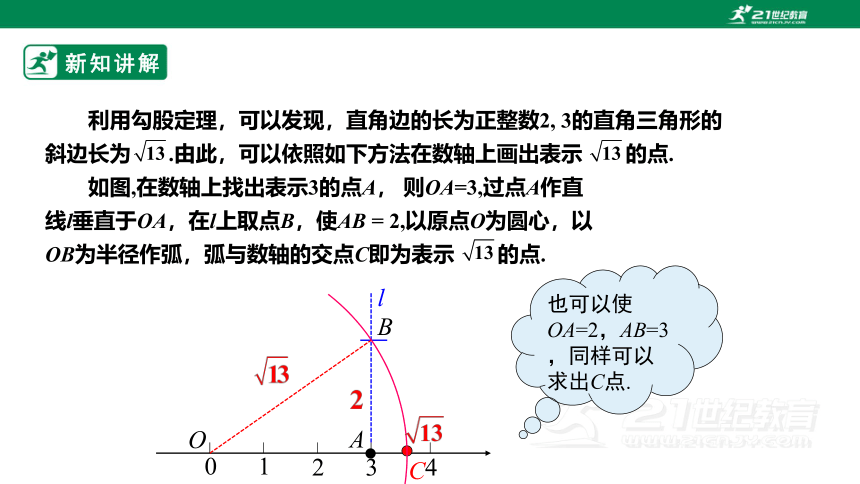
利用勾股定理,可以发现,直角边的长为正整数2, 3的直角三角形的斜边长为 .由此,可以依照如下方法在数轴上画出表示 的点.
如图,在数轴上找出表示3的点A, 则OA=3,过点A作直
线l垂直于OA,在l上取点B,使AB = 2,以原点O为圆心,以
OB为半径作弧,弧与数轴的交点C即为表示 的点.
0
1
2
3
4
l
A
B
C
O
也可以使OA=2,AB=3,同样可以求出C点.
新知讲解
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
归纳总结
新知讲解
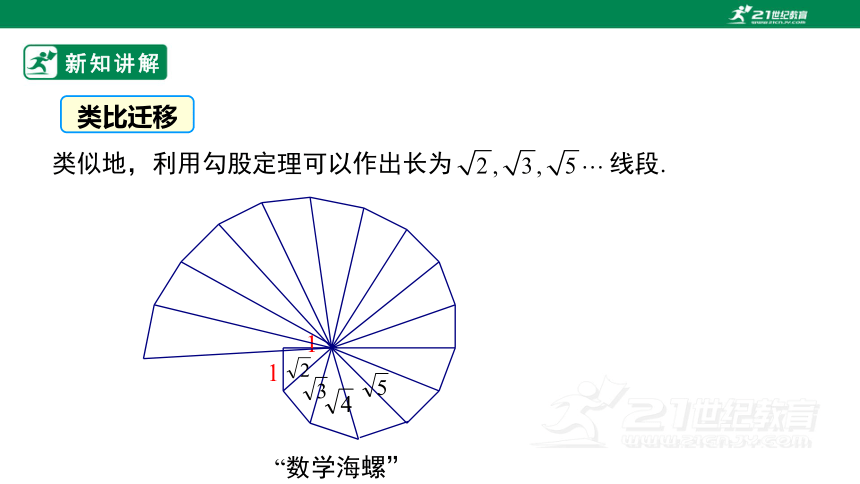
“数学海螺”
类似地,利用勾股定理可以作出长为 线段.
1
1
类比迁移
例题讲解
0
1
2
3
4
l
A
B
C
例1 在数轴上作出表示 的点.
作法:
(1)在数轴上找到点A,使OA=1;
(2)过点A作直线垂直于OA,在直线上取点B,
使AB=4,那么OB= ;
(3)以原点O为圆心,以OB为半径作
弧,弧与数轴交于点C,则OC= .
如图,在数轴上,点C为表示 的点.
变式练习
1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边长为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
易错点拨:求点表示的数时注意画弧的起点不从原点起,则所表示的数不是斜边长.
新知讲解
三、勾股定理与网格
画一画 在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中以A出发分别画出长度为 的线段AB.
B
B
B
例题讲解
例2 在如图所示的6×8的网格中,每个小正方形的边长都为1,写出格点△ABC各顶点的坐标,并求出此三角形的周长.
解:由题图得A(2,2),B(-2,-1),C(3,-2).
由勾股定理得
∴△ABC的周长为
归纳:勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
例题讲解
例3 如图,在△ABC中,∠C=60°,AB=14,AC
=10. 求BC的长.
解:如图,过点A作AD⊥BC于D.
∵∠ADC=90°,∠C=60°,∴CD= AC=5.
在Rt△ACD中,
AD
在Rt△ABD中,
BD
∴BC=BD+CD=11+5=16.
例题讲解
例4 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理,得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得 x2+ 42=(8-x)2,
解得 x=3.
即EC的长为3cm.
要用到方程思想
例题讲解
例5 如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.
解:如图,延长AD、BC交于E.
∵∠B=90°,∠A=60°,
∴∠E=90°-60°=30°,
在Rt△ABE和Rt△CDE中,
∵AB=2,CD=1,
∴AE=2AB=2×2=4,CE=2CD=2×1=2,
由勾股定理得
E
D
C
B
A
补形法求面积
课堂小结
利用勾股定理作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
拓展提高
1.如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段________条.
8
拓展提高
解:∵AB=AD=8cm,∠A=60°,
∴△ABD是等边三角形.
∵∠ADC=150°,
∴∠CDB=150°-60°=90°,
∴△BCD是直角三角形.
又∵四边形的周长为32cm,
∴CD+BC=32-AD-AB=32-8-8=16(cm).
设CD=xcm,则BC=(16-x)cm,
由勾股定理得82+x2=(16-x)2,
解得x=6. ∴S△BCD= ×6×8=24(cm2).
2.如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.
拓展提高
解:如图,
3.若△ABC三边的长分别为 (a>0),请利用图中的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
∴△ABC即为所求,
A
B
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.1勾股定理(3)
人教版八年级下册
教学目标
2. 能利用勾股定理在数轴上作出表示无理数的点.
1. 会用勾股定理解决简单的实际问题,建立数形结合的思想.
3.灵活运用勾股定理进行计算,并会运用勾股定理解决相应的折叠问题.
新知导入
欣赏下面海螺的图片:
在数学中也有这样一幅美丽的“海螺型”图案,
如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?
新知讲解
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
知识点 1
证明“HL”
已知:如图,在Rt△ABC 和Rt△A′B′ C′中,
∠C=∠C′=90°,AB=A′B ′,AC=A′C′ .
求证:△ABC≌△ A′B′ C′ .
新知讲解
′
′
′
′
′
′
证明:在Rt△ABC 和Rt△A ′B′ C′中,∠C=∠C′=90°,
根据勾股定理,得
A
B
C
A
B
C′
′
′
∵ AB=A′B′ ,
AC=A′C′ ,
∴ BC=B′C′ .
∴ △ ABC≌ △A ′B′ C′ (SSS).
新知讲解
-1 0 1 2 3
问题1 你能在数轴上画出表示 的点吗? 呢?
用同样的方法作 呢?
二、勾股定理与数轴
提示:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
新知讲解
利用勾股定理,可以发现,直角边的长为正整数2, 3的直角三角形的斜边长为 .由此,可以依照如下方法在数轴上画出表示 的点.
如图,在数轴上找出表示3的点A, 则OA=3,过点A作直
线l垂直于OA,在l上取点B,使AB = 2,以原点O为圆心,以
OB为半径作弧,弧与数轴的交点C即为表示 的点.
0
1
2
3
4
l
A
B
C
O
也可以使OA=2,AB=3,同样可以求出C点.
新知讲解
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
归纳总结
新知讲解
“数学海螺”
类似地,利用勾股定理可以作出长为 线段.
1
1
类比迁移
例题讲解
0
1
2
3
4
l
A
B
C
例1 在数轴上作出表示 的点.
作法:
(1)在数轴上找到点A,使OA=1;
(2)过点A作直线垂直于OA,在直线上取点B,
使AB=4,那么OB= ;
(3)以原点O为圆心,以OB为半径作
弧,弧与数轴交于点C,则OC= .
如图,在数轴上,点C为表示 的点.
变式练习
1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边长为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
易错点拨:求点表示的数时注意画弧的起点不从原点起,则所表示的数不是斜边长.
新知讲解
三、勾股定理与网格
画一画 在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中以A出发分别画出长度为 的线段AB.
B
B
B
例题讲解
例2 在如图所示的6×8的网格中,每个小正方形的边长都为1,写出格点△ABC各顶点的坐标,并求出此三角形的周长.
解:由题图得A(2,2),B(-2,-1),C(3,-2).
由勾股定理得
∴△ABC的周长为
归纳:勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
例题讲解
例3 如图,在△ABC中,∠C=60°,AB=14,AC
=10. 求BC的长.
解:如图,过点A作AD⊥BC于D.
∵∠ADC=90°,∠C=60°,∴CD= AC=5.
在Rt△ACD中,
AD
在Rt△ABD中,
BD
∴BC=BD+CD=11+5=16.
例题讲解
例4 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理,得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得 x2+ 42=(8-x)2,
解得 x=3.
即EC的长为3cm.
要用到方程思想
例题讲解
例5 如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.
解:如图,延长AD、BC交于E.
∵∠B=90°,∠A=60°,
∴∠E=90°-60°=30°,
在Rt△ABE和Rt△CDE中,
∵AB=2,CD=1,
∴AE=2AB=2×2=4,CE=2CD=2×1=2,
由勾股定理得
E
D
C
B
A
补形法求面积
课堂小结
利用勾股定理作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
拓展提高
1.如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段________条.
8
拓展提高
解:∵AB=AD=8cm,∠A=60°,
∴△ABD是等边三角形.
∵∠ADC=150°,
∴∠CDB=150°-60°=90°,
∴△BCD是直角三角形.
又∵四边形的周长为32cm,
∴CD+BC=32-AD-AB=32-8-8=16(cm).
设CD=xcm,则BC=(16-x)cm,
由勾股定理得82+x2=(16-x)2,
解得x=6. ∴S△BCD= ×6×8=24(cm2).
2.如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.
拓展提高
解:如图,
3.若△ABC三边的长分别为 (a>0),请利用图中的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
∴△ABC即为所求,
A
B
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
