10.1.1两角和与差的余弦公式课件-2022-2023学年高一下学期数学苏教版(2019)必修第二册(共19张PPT)
文档属性
| 名称 | 10.1.1两角和与差的余弦公式课件-2022-2023学年高一下学期数学苏教版(2019)必修第二册(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 873.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 10:43:05 | ||
图片预览





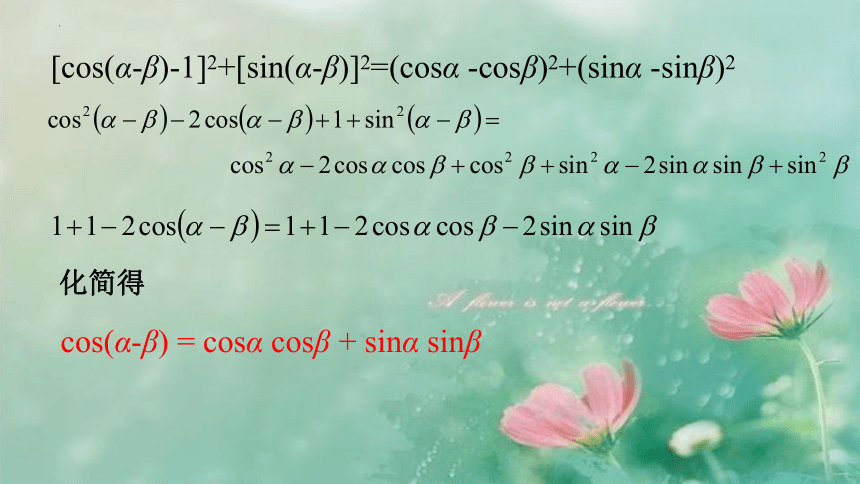
文档简介
(共19张PPT)
两角和与差的余弦公式
1.熟悉两角差的余弦公式的推导过程.
2.熟记两角差的余弦公式,并能灵活运用.
学习目标:
思考:cos 15 ° =cos(60°- 45 °) = cos60° - cos45 °成立吗
思考:设α,β为两个任意角,你能判断下面的恒成立吗
引入:cos 15 ° = ?
A
o
y
x
P
x
y
O
O
x
y
P1
A1
A
P
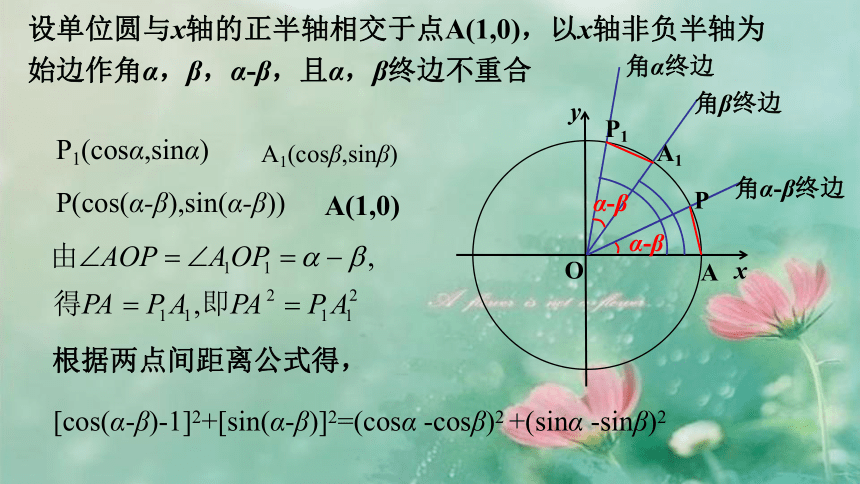
设单位圆与x轴的正半轴相交于点A(1,0),以x轴非负半轴为始边作角α,β,α-β,且α,β终边不重合
角α-β终边
角β终边
角α终边
P1(cosα,sinα)
P(cos(α-β),sin(α-β))
根据两点间距离公式得,
α-β
α-β
[cos(α-β)-1]2+[sin(α-β)]2=(cosα -cosβ)2 +(sinα -sinβ)2
A1(cosβ,sinβ)
A(1,0)
化简得
cos(α-β) = cosα cosβ + sinα sinβ
[cos(α-β)-1]2+[sin(α-β)]2=(cosα -cosβ)2+(sinα -sinβ)2
两角差的余弦公式
差角的余弦公式
①任意角; ②同名积; ③符号反.
说一说:1、公式的结构特点:
对于任意的角α、β
两角和的余弦公式
用-β代替β的换元方法是三角变换中常用的方法
注意:
记清公式的结构特征,尤其是符号规律:
两角对应,CCSS,符号相反.
两角和与差的余弦公式:
cos(α-β)=cosαcosβ+sinαsin β(C(α -β ))
cos(α+β)=cosαcosβ-sinαsinβ (C(α +β ))
形成结论
我们再回到之前提出的问题,如何用差角余弦公式
求 的值。
收获: 1、把非特殊角拆分成特殊角的差.
2、公式的直接应用.
例1.利用公式C(α-β)证明:
例题探究
(1) (2)
证明:
例题探究
利用公式给角求值
例2 计算:(1) cos( -15°);
(2) cos105°cos15°+ sin105°sin15°.
(2)原式=cos(105°-15°)=cos90°=0
跟踪训练
利用公式给角求值
求下列的值: cos75°cos15°+ sin75°sin15°;
解:
例题探究3
整体法给值求值问题
跟踪训练
两角和与差的余弦公式:
cos(α-β)=cosαcosβ+sinαsin β(C(α -β ))
cos(α+β)=cosαcosβ-sinαsinβ (C(α +β ))
两角差的余弦公式应用:
给角求值
给值求值
课堂小结
当堂检测
C
C
谢 谢
两角和与差的余弦公式
1.熟悉两角差的余弦公式的推导过程.
2.熟记两角差的余弦公式,并能灵活运用.
学习目标:
思考:cos 15 ° =cos(60°- 45 °) = cos60° - cos45 °成立吗
思考:设α,β为两个任意角,你能判断下面的恒成立吗
引入:cos 15 ° = ?
A
o
y
x
P
x
y
O
O
x
y
P1
A1
A
P
设单位圆与x轴的正半轴相交于点A(1,0),以x轴非负半轴为始边作角α,β,α-β,且α,β终边不重合
角α-β终边
角β终边
角α终边
P1(cosα,sinα)
P(cos(α-β),sin(α-β))
根据两点间距离公式得,
α-β
α-β
[cos(α-β)-1]2+[sin(α-β)]2=(cosα -cosβ)2 +(sinα -sinβ)2
A1(cosβ,sinβ)
A(1,0)
化简得
cos(α-β) = cosα cosβ + sinα sinβ
[cos(α-β)-1]2+[sin(α-β)]2=(cosα -cosβ)2+(sinα -sinβ)2
两角差的余弦公式
差角的余弦公式
①任意角; ②同名积; ③符号反.
说一说:1、公式的结构特点:
对于任意的角α、β
两角和的余弦公式
用-β代替β的换元方法是三角变换中常用的方法
注意:
记清公式的结构特征,尤其是符号规律:
两角对应,CCSS,符号相反.
两角和与差的余弦公式:
cos(α-β)=cosαcosβ+sinαsin β(C(α -β ))
cos(α+β)=cosαcosβ-sinαsinβ (C(α +β ))
形成结论
我们再回到之前提出的问题,如何用差角余弦公式
求 的值。
收获: 1、把非特殊角拆分成特殊角的差.
2、公式的直接应用.
例1.利用公式C(α-β)证明:
例题探究
(1) (2)
证明:
例题探究
利用公式给角求值
例2 计算:(1) cos( -15°);
(2) cos105°cos15°+ sin105°sin15°.
(2)原式=cos(105°-15°)=cos90°=0
跟踪训练
利用公式给角求值
求下列的值: cos75°cos15°+ sin75°sin15°;
解:
例题探究3
整体法给值求值问题
跟踪训练
两角和与差的余弦公式:
cos(α-β)=cosαcosβ+sinαsin β(C(α -β ))
cos(α+β)=cosαcosβ-sinαsinβ (C(α +β ))
两角差的余弦公式应用:
给角求值
给值求值
课堂小结
当堂检测
C
C
谢 谢
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
