7.1 行星的运动 课件 (共20张PPT) 高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 7.1 行星的运动 课件 (共20张PPT) 高一下学期物理人教版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 34.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-16 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
§7.1 行星的运动
第七章 万有引力与宇宙航行
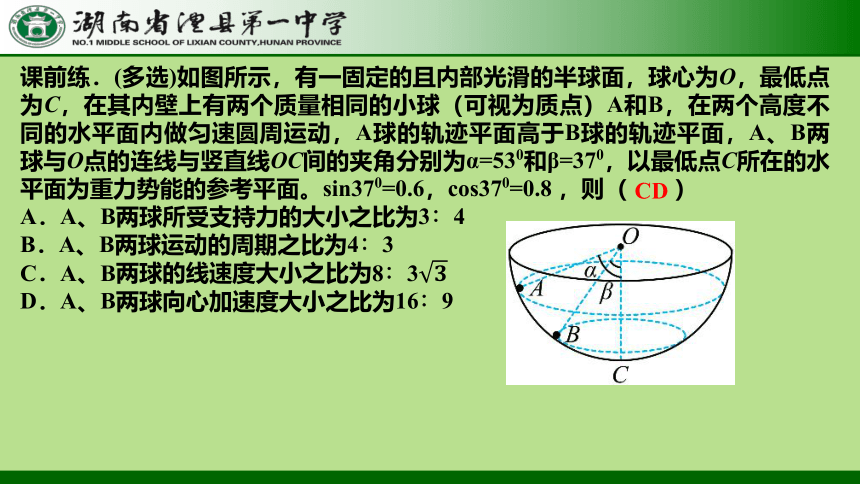
课前练.(多选)如图所示,有一固定的且内部光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=530和β=370,以最低点C所在的水平面为重力势能的参考平面。sin370=0.6,cos370=0.8 ,则( )
A.A、B两球所受支持力的大小之比为3∶4
B.A、B两球运动的周期之比为4∶3
C.A、B两球的线速度大小之比为8∶3
D.A、B两球向心加速度大小之比为16∶9
CD
不同行星都在各自的轨道上绕太阳运行,行星运行的轨道有怎样的特点?行星绕太阳运行的周期与距离太阳的远近是否存在某种关系?
阅读教材(3分钟):
P46→P48→P44
了解地心说与日心说
天文学简史
开普勒定律
阅读教材(5分钟):
P44→P45
了解开普勒三定律,并说明各定律:
研究内容
研究对象
理解应用
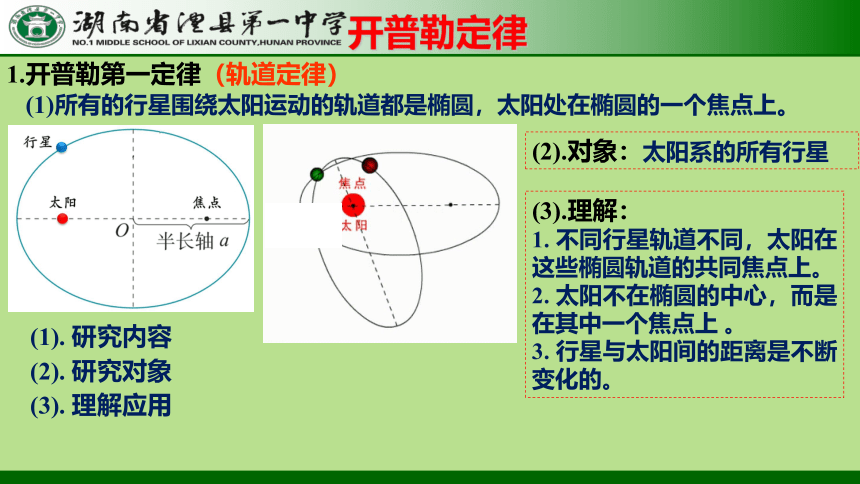
1.开普勒第一定律(轨道定律)
(1)所有的行星围绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
(2).对象:太阳系的所有行星
(1). 研究内容
(2). 研究对象
(3). 理解应用
(3).理解:
1. 不同行星轨道不同,太阳在这些椭圆轨道的共同焦点上。
2. 太阳不在椭圆的中心,而是在其中一个焦点上 。
3. 行星与太阳间的距离是不断变化的。
开普勒定律
绘制椭圆
思考:保持绳长不变,当两焦点不断靠近时,椭圆形状如何变化? 焦点重合时,半长轴转变为什么?
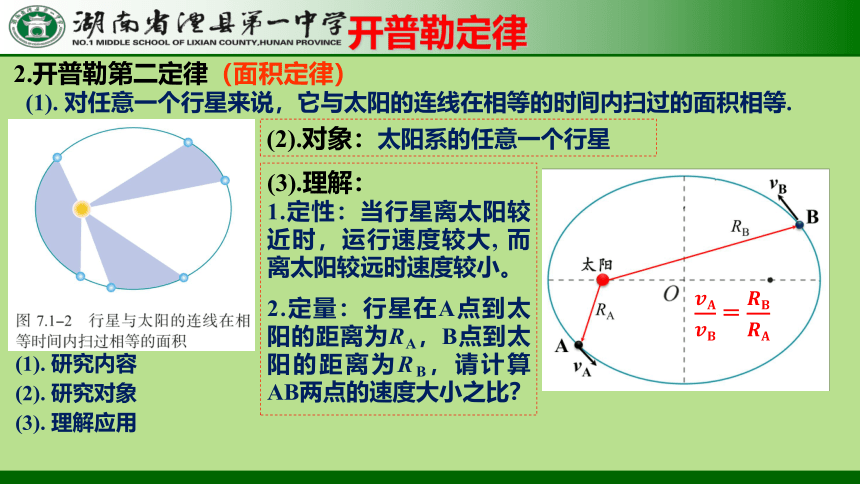
2.开普勒第二定律(面积定律)
(1). 对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等.
(1). 研究内容
(2). 研究对象
(3). 理解应用
(2).对象:太阳系的任意一个行星
(3).理解:
1.定性:当行星离太阳较近时,运行速度较大, 而离太阳较远时速度较小。
2.定量:行星在A点到太阳的距离为RA,B点到太阳的距离为RB,请计算AB两点的速度大小之比?
=
开普勒定律
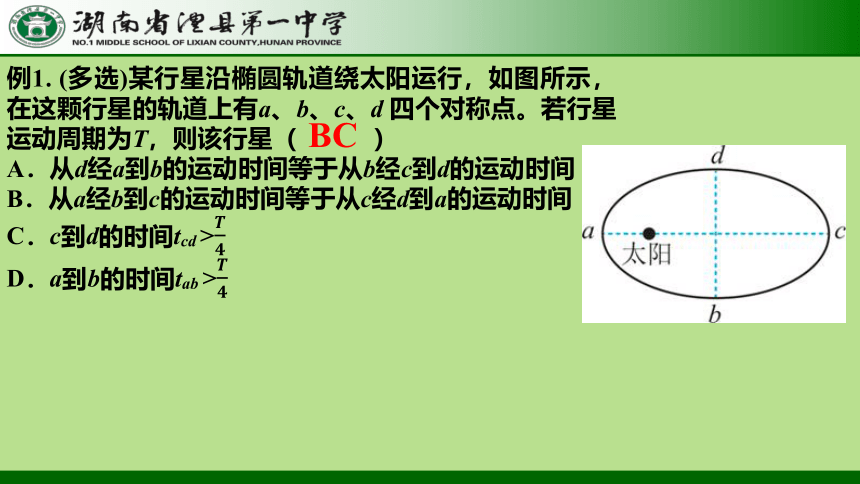
例1. (多选)某行星沿椭圆轨道绕太阳运行,如图所示,在这颗行星的轨道上有a、b、c、d 四个对称点。若行星运动周期为T,则该行星( )
A.从d经a到b的运动时间等于从b经c到d的运动时间
B.从a经b到c的运动时间等于从c经d到a的运动时间
C.c到d的时间tcd >
D.a到b的时间tab >
BC
3.(多选)在天文学上,春分、夏至、秋分、冬至将一年分为春、夏、秋、冬四季.如图,从地球绕太阳的运动规律入手,下列判断正确的是( )
A.在1月初,地球绕太阳的运行速率较大
B.在7月初,地球绕太阳的运行速率较大
C.在北半球,春、夏两季与秋、冬两季时间相等
D.在北半球,春、夏两季比秋、冬两季时间长
AD
3.开普勒第三定律(周期定律)
(1).所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
(2).对象:1. 太阳系任意一个行星
(1). 研究内容
(2). 研究对象
(3). 理解应用
(3).理解:
比值 k 是一个对所有行星都相同的常量,
与行星无关而只与太阳有关。
T
2. 太阳系任意两个行星
开普勒定律
[针对训练1] 火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知( )
A.太阳位于木星运行轨道的中心
B.火星和木星绕太阳运行速度的大小始终相等
C.火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方
D.相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积
C
系统集成 第60页
(1)“在相等的时间内,行星与太阳连线扫过的面积相等”是对于同一颗行星而言的.对不同行星则不成立.
(2)公式=k中的比例常数k对绕同一中心天体运转的星体是相同的.对不同的星系比例常数k一般是不同的.
[例2] 某宇宙飞船进入一个围绕太阳运行的近似圆轨道,如果轨道半径是地球轨道半径的9倍,那么宇宙飞船绕太阳运行的周期为(地球绕太阳运行的周期为1年)( )
A.3年 B.9年
C.27年 D.54年
C
系统集成 第60页
2.(多选)关于开普勒行星运动的公式=k,以下理解正确的是( )
A.k是一个与行星无关的量
B.T表示行星运动的自转周期
C.T表示行星运动的公转周期
D.若地球绕太阳运行轨道的半长轴为a地、公转周期为T地,月球绕地球运行轨道的半长轴为a月、公转周期为T月,则
AC
系统集成 第61页
实际上行星的轨道是一个不蛮椭的椭圆,
高中阶段按圆轨道处理:
从开普勒第二定律可知,行星绕太阳做圆周运动的角速度(或线速度)大小不变,即行星做匀速圆周运动。
在圆轨道的基础上,请结合开普勒定律分析行星是否做匀速圆周运动?
课堂小结
1.开普勒第一定律(轨道定律)
(1)所有的行星围绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2.开普勒第二定律(面积定律)
(1). 对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等.
3.开普勒第三定律(周期定律)
(1).所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
=
1.地球公转轨道的半径在天文学上常用来作为长度单位,叫作天文单位,用来量度太阳系内天体与太阳的距离。(这只是个粗略的说法。在天文学中,“天文单位”有严格的定义,用符号表示。)已知火星公转的轨道半径是1.5,根据开普勒第三定律,火星公转的周期是多少个地球日?
教材 第48页第1题
[针对训练2] (多选)某彗星绕太阳运动的轨道是比较扁的椭圆,下列说法正确的是( )
A.彗星在近日点的速率大于在远日点的速率
B.彗星在近日点的角速度大于在远日点的角速度
C.若彗星运转周期为76年,则它的轨道的半长轴是地球公转轨道的半长轴的2倍
D.若彗星运转周期为76年,则它的轨道的半长轴是地球公转轨道的半长轴的76倍
ABC
系统集成 第61页
补充.如图所示,一颗近地卫星甲的轨道半径近似等于地球半径R,另一颗卫星乙的轨道是椭圆,与近地圆轨道相切于A点,远地点B距地心的距离是3R,已知引力常量G,且两卫星不会相撞。求:
(1)椭圆轨道上卫星乙在近地点A和远地点B的线速度大小的比值。
(2)若近地卫星甲的周期为T,求椭圆轨道卫星乙从A到B的时间?
(1) ;(2)tAB =T
§7.1 行星的运动
第七章 万有引力与宇宙航行
课前练.(多选)如图所示,有一固定的且内部光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=530和β=370,以最低点C所在的水平面为重力势能的参考平面。sin370=0.6,cos370=0.8 ,则( )
A.A、B两球所受支持力的大小之比为3∶4
B.A、B两球运动的周期之比为4∶3
C.A、B两球的线速度大小之比为8∶3
D.A、B两球向心加速度大小之比为16∶9
CD
不同行星都在各自的轨道上绕太阳运行,行星运行的轨道有怎样的特点?行星绕太阳运行的周期与距离太阳的远近是否存在某种关系?
阅读教材(3分钟):
P46→P48→P44
了解地心说与日心说
天文学简史
开普勒定律
阅读教材(5分钟):
P44→P45
了解开普勒三定律,并说明各定律:
研究内容
研究对象
理解应用
1.开普勒第一定律(轨道定律)
(1)所有的行星围绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
(2).对象:太阳系的所有行星
(1). 研究内容
(2). 研究对象
(3). 理解应用
(3).理解:
1. 不同行星轨道不同,太阳在这些椭圆轨道的共同焦点上。
2. 太阳不在椭圆的中心,而是在其中一个焦点上 。
3. 行星与太阳间的距离是不断变化的。
开普勒定律
绘制椭圆
思考:保持绳长不变,当两焦点不断靠近时,椭圆形状如何变化? 焦点重合时,半长轴转变为什么?
2.开普勒第二定律(面积定律)
(1). 对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等.
(1). 研究内容
(2). 研究对象
(3). 理解应用
(2).对象:太阳系的任意一个行星
(3).理解:
1.定性:当行星离太阳较近时,运行速度较大, 而离太阳较远时速度较小。
2.定量:行星在A点到太阳的距离为RA,B点到太阳的距离为RB,请计算AB两点的速度大小之比?
=
开普勒定律
例1. (多选)某行星沿椭圆轨道绕太阳运行,如图所示,在这颗行星的轨道上有a、b、c、d 四个对称点。若行星运动周期为T,则该行星( )
A.从d经a到b的运动时间等于从b经c到d的运动时间
B.从a经b到c的运动时间等于从c经d到a的运动时间
C.c到d的时间tcd >
D.a到b的时间tab >
BC
3.(多选)在天文学上,春分、夏至、秋分、冬至将一年分为春、夏、秋、冬四季.如图,从地球绕太阳的运动规律入手,下列判断正确的是( )
A.在1月初,地球绕太阳的运行速率较大
B.在7月初,地球绕太阳的运行速率较大
C.在北半球,春、夏两季与秋、冬两季时间相等
D.在北半球,春、夏两季比秋、冬两季时间长
AD
3.开普勒第三定律(周期定律)
(1).所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
(2).对象:1. 太阳系任意一个行星
(1). 研究内容
(2). 研究对象
(3). 理解应用
(3).理解:
比值 k 是一个对所有行星都相同的常量,
与行星无关而只与太阳有关。
T
2. 太阳系任意两个行星
开普勒定律
[针对训练1] 火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知( )
A.太阳位于木星运行轨道的中心
B.火星和木星绕太阳运行速度的大小始终相等
C.火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方
D.相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积
C
系统集成 第60页
(1)“在相等的时间内,行星与太阳连线扫过的面积相等”是对于同一颗行星而言的.对不同行星则不成立.
(2)公式=k中的比例常数k对绕同一中心天体运转的星体是相同的.对不同的星系比例常数k一般是不同的.
[例2] 某宇宙飞船进入一个围绕太阳运行的近似圆轨道,如果轨道半径是地球轨道半径的9倍,那么宇宙飞船绕太阳运行的周期为(地球绕太阳运行的周期为1年)( )
A.3年 B.9年
C.27年 D.54年
C
系统集成 第60页
2.(多选)关于开普勒行星运动的公式=k,以下理解正确的是( )
A.k是一个与行星无关的量
B.T表示行星运动的自转周期
C.T表示行星运动的公转周期
D.若地球绕太阳运行轨道的半长轴为a地、公转周期为T地,月球绕地球运行轨道的半长轴为a月、公转周期为T月,则
AC
系统集成 第61页
实际上行星的轨道是一个不蛮椭的椭圆,
高中阶段按圆轨道处理:
从开普勒第二定律可知,行星绕太阳做圆周运动的角速度(或线速度)大小不变,即行星做匀速圆周运动。
在圆轨道的基础上,请结合开普勒定律分析行星是否做匀速圆周运动?
课堂小结
1.开普勒第一定律(轨道定律)
(1)所有的行星围绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2.开普勒第二定律(面积定律)
(1). 对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等.
3.开普勒第三定律(周期定律)
(1).所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
=
1.地球公转轨道的半径在天文学上常用来作为长度单位,叫作天文单位,用来量度太阳系内天体与太阳的距离。(这只是个粗略的说法。在天文学中,“天文单位”有严格的定义,用符号表示。)已知火星公转的轨道半径是1.5,根据开普勒第三定律,火星公转的周期是多少个地球日?
教材 第48页第1题
[针对训练2] (多选)某彗星绕太阳运动的轨道是比较扁的椭圆,下列说法正确的是( )
A.彗星在近日点的速率大于在远日点的速率
B.彗星在近日点的角速度大于在远日点的角速度
C.若彗星运转周期为76年,则它的轨道的半长轴是地球公转轨道的半长轴的2倍
D.若彗星运转周期为76年,则它的轨道的半长轴是地球公转轨道的半长轴的76倍
ABC
系统集成 第61页
补充.如图所示,一颗近地卫星甲的轨道半径近似等于地球半径R,另一颗卫星乙的轨道是椭圆,与近地圆轨道相切于A点,远地点B距地心的距离是3R,已知引力常量G,且两卫星不会相撞。求:
(1)椭圆轨道上卫星乙在近地点A和远地点B的线速度大小的比值。
(2)若近地卫星甲的周期为T,求椭圆轨道卫星乙从A到B的时间?
(1) ;(2)tAB =T
