【核心素养目标】26.2.2用列表或画树状图形等可能情形下的概率 教学设计
文档属性
| 名称 | 【核心素养目标】26.2.2用列表或画树状图形等可能情形下的概率 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 16:03:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数学26.2.2用列表或画树状图形等可能情形下的概率教学设计
课题 26.2.2用列表或画树状图形等可能情形下的概率 单元 第26单元 学科 数学 年级 九
教材分析 在上节学习了求简单概率的基础上,进一步学习了计算概率方法,能够进行简单的概率计算;掌握用树状图法或者列举法求概率的方法,熟练运用树状图解决实际问题。
核心素养分析 本节利用树状图法或列表法求比较复杂事件的概率,总结了树状图法或列表法求概率的步骤,培养了学生随机性的认识,发展了学生应用概率知识的意识。
学习目标 1.在求简单事件概率基础上,进一步学习计算概率方法,能够进行简单的概率计算;2.掌握用树状图法或列表法求概率的方法,熟练运用树状图或列表法解决实际问题。
重点 在求简单事件概率基础上,进一步学习计算概率方法,能够进行简单的概率计算
难点 掌握用树状图法或列表法求概率的方法,熟练运用树状图或列表法解决实际问题。
教学过程
教学环节 教师活动 学生活动 设计意图
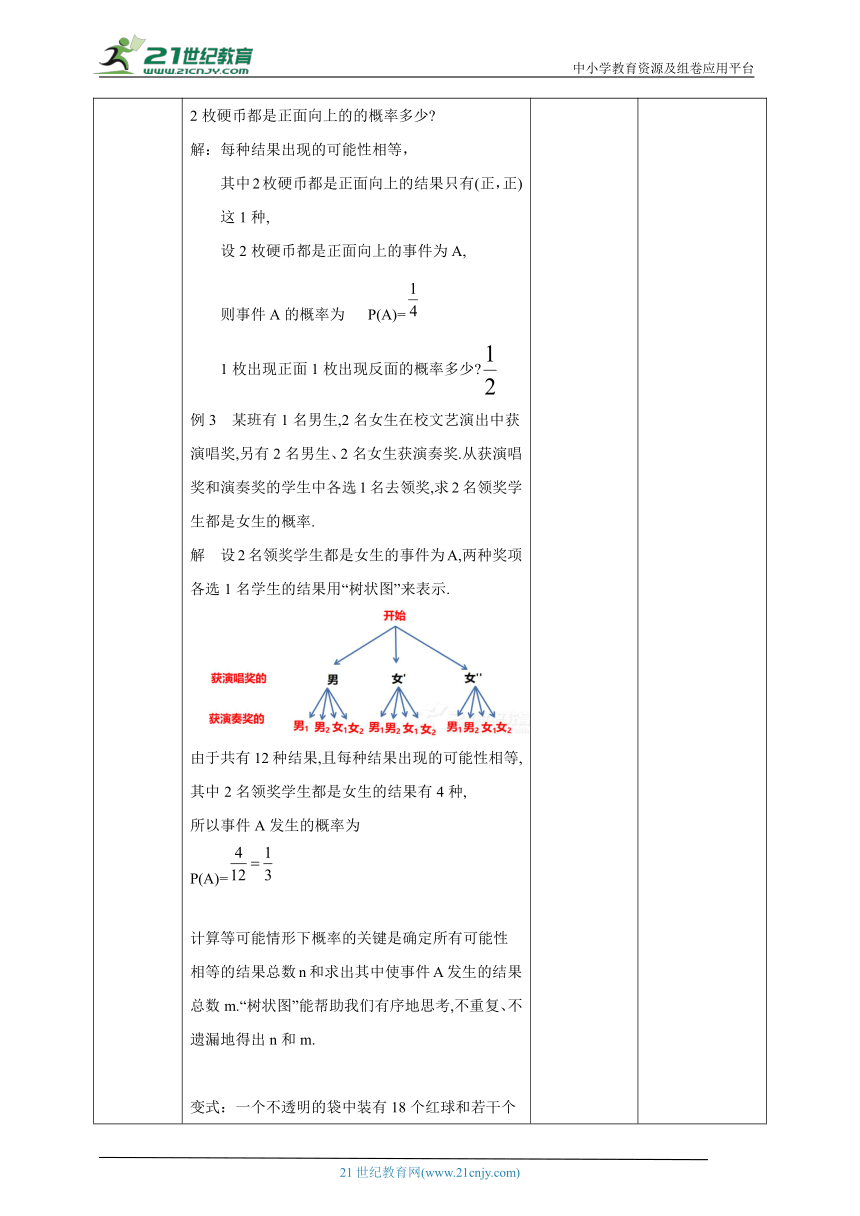
导入新课 概率的性质有哪些? 当A是必然事件时,P(A)=1;当A是不可能事件时,P(A)=0。所以有0≤P(A)≤1.一般地,对任何随机事件A,它的概率P(A)满足0讲授新课 例2 同时抛掷2枚均匀的硬币一次,求2枚硬币都是正面向上的概率.解 同时抛掷2枚硬币一次,可能出现如下4种不同的结果:(正,正),(正,反),(反,正),(反,反).我们可以用“树状图”来表示上述所有可能出现的结果2枚硬币都是正面向上的的概率多少 解:每种结果出现的可能性相等, 其中2枚硬币都是正面向上的结果只有(正,正)这1种, 设2枚硬币都是正面向上的事件为A, 则事件A的概率为 P(A)=1枚出现正面1枚出现反面的概率多少 例3 某班有1名男生,2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各选1名去领奖,求2名领奖学生都是女生的概率.解 设2名领奖学生都是女生的事件为A,两种奖项各选1名学生的结果用“树状图”来表示.由于共有12种结果,且每种结果出现的可能性相等,其中2名领奖学生都是女生的结果有4种,所以事件A发生的概率为P(A)=计算等可能情形下概率的关键是确定所有可能性相等的结果总数n和求出其中使事件A发生的结果总数m.“树状图”能帮助我们有序地思考,不重复、不遗漏地得出n和m. 变式:一个不透明的袋中装有18个红球和若干个白球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是红球的概率是 。求袋中总共有多少个球 解:设袋中有x个球,∵袋中装有18个红球,从中任意摸出一个球是红球的概率是∴解得:x =30 即袋中总共有30个球。画树形图求概率的基本步骤(1)确定一次试验的步骤;(2)画树状图列举一次试验的所有等可能结果;(3)确定随机事件A包含的结果数m,试验的所有可能结果数n;(4)用概率公式计算.例4 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1 ,2,…,6。试分别计算如下各随机事件的概率:(1)抛出的点数之和等于8;(2)抛出的点数之和等于12。分析:为了解决这个问题,我们首先要弄清楚一共有多少个可能结果。虽然同时抛掷2枚均匀的散子一次,点数之和可能为2,3 ,…,12中的任何一种,但是它们并不是发生的所有可能结果。所有可能结果有哪些呢 我们知道:第1枚骰子可能掷出1,2,…,6 中的每一种情况,第2枚骰子也可能掷出1,2,…,6中的每一种情况,而且无论第1枚骰子掷出1,2,…,6中的哪一种情况,第2枚骰子都可能掷出1,2,…,6中的任一种情况。所以我们用“列表法”列出所有的可能结果如下:解 从上面表格中可以看出,同时抛掷2枚骰子一次,所有可能出现的结果有36种。由于骰子是均匀的,所以每个结果出现的可能性相等。(1)抛出的点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8这个事件发生的概率为;(2)抛出的点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12这个事件发生的概率为。当一个试验有两个相关因素,且所有可能的结果较多时,为不重不漏地列出所有可能的结果,通常采用列表法从这个例子中再次体会弄清楚所有可能结果的重要性.如同“树状图”一样,“列表法”也能帮助我们有序地思考。用列表法求概率步骤:1.列表;2.通过表格计数;3.利用概率公式计算出事件的概率. 学生学习树状图法求概率的方法 总结用树状图法或列表法求概率的步骤。学生利用列表法求概率,然后小组讨论交流,教师总结。总结列表法求概率的步骤 理解树状图法求概率的规律。 锻炼学生用树状图法求概率的规律培养学生运用列表法求概率的方法。培养学生运用列表法求概率的步骤。
课堂练习 1.不透明的布袋中有红、黄、蓝3种颜色不同的小球各1个,它们除颜色不同外其余完全相同,先从中随机摸出1个,记录下它的颜色,将它放回布袋并搅匀,再从中随机摸出1个,记录下颜色,那么这两次摸出小球的颜色都为蓝色的概率是__________. 解:树状图如图所示: 共有9种等可能情况,其中两次摸出小球的颜色都为蓝色有1种,∴这两次摸出小球的颜色都为蓝色的概率是。 2.在4件同型号的产品A,B,C,D中,A ,B,C为合格产品,D为不合格产品.(1)从这4件产品中随机抽取1件进行检测,直接写出抽到合格品的概率;(2)从这4件产品中任抽取一件检测后放回,再抽取一件进行检测,请用画树状图法或列表法求两次抽到的都是合格品的概率.解:(1)∵4件同型号的产品A,B,C,D中,A,B,C为合格产品,D为不合格产品,∴合格品的概率为:P=.(2)如树状图下图: P=3.将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.(1)从中随机抽出一张牌,牌面数字小于3的概率是______;(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是3的倍数的概率.解:(1)四张牌中任抽取一张,所有等可能的结果有4种,其中牌面数字小于3的结果有2种,则从中随机抽出一张牌,牌面数字小于3的概率是 ;(2)解:列表如下:由表知,所有可能的结果数有16种,其中组成的两位数是3的位数的有5种,则组成的两位数恰好是3的倍数的概率是: . 学生熟练运用本节树状图或列表法求概率步骤,互相补充,教师订正答案,最后总结本节内容。 练习是为了巩固学生所学的新知,教会学生运用树状图法或列表法求概率的步骤来解决问题。
课堂小结 学生先发言总结本节用树状图法或列表法求概率的步骤,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:26.2.2等可能情形下的简单概率计算1.树状图法2.列表法
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学26.2.2用列表或画树状图形等可能情形下的概率教学设计
课题 26.2.2用列表或画树状图形等可能情形下的概率 单元 第26单元 学科 数学 年级 九
教材分析 在上节学习了求简单概率的基础上,进一步学习了计算概率方法,能够进行简单的概率计算;掌握用树状图法或者列举法求概率的方法,熟练运用树状图解决实际问题。
核心素养分析 本节利用树状图法或列表法求比较复杂事件的概率,总结了树状图法或列表法求概率的步骤,培养了学生随机性的认识,发展了学生应用概率知识的意识。
学习目标 1.在求简单事件概率基础上,进一步学习计算概率方法,能够进行简单的概率计算;2.掌握用树状图法或列表法求概率的方法,熟练运用树状图或列表法解决实际问题。
重点 在求简单事件概率基础上,进一步学习计算概率方法,能够进行简单的概率计算
难点 掌握用树状图法或列表法求概率的方法,熟练运用树状图或列表法解决实际问题。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 概率的性质有哪些? 当A是必然事件时,P(A)=1;当A是不可能事件时,P(A)=0。所以有0≤P(A)≤1.一般地,对任何随机事件A,它的概率P(A)满足0
课堂练习 1.不透明的布袋中有红、黄、蓝3种颜色不同的小球各1个,它们除颜色不同外其余完全相同,先从中随机摸出1个,记录下它的颜色,将它放回布袋并搅匀,再从中随机摸出1个,记录下颜色,那么这两次摸出小球的颜色都为蓝色的概率是__________. 解:树状图如图所示: 共有9种等可能情况,其中两次摸出小球的颜色都为蓝色有1种,∴这两次摸出小球的颜色都为蓝色的概率是。 2.在4件同型号的产品A,B,C,D中,A ,B,C为合格产品,D为不合格产品.(1)从这4件产品中随机抽取1件进行检测,直接写出抽到合格品的概率;(2)从这4件产品中任抽取一件检测后放回,再抽取一件进行检测,请用画树状图法或列表法求两次抽到的都是合格品的概率.解:(1)∵4件同型号的产品A,B,C,D中,A,B,C为合格产品,D为不合格产品,∴合格品的概率为:P=.(2)如树状图下图: P=3.将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.(1)从中随机抽出一张牌,牌面数字小于3的概率是______;(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是3的倍数的概率.解:(1)四张牌中任抽取一张,所有等可能的结果有4种,其中牌面数字小于3的结果有2种,则从中随机抽出一张牌,牌面数字小于3的概率是 ;(2)解:列表如下:由表知,所有可能的结果数有16种,其中组成的两位数是3的位数的有5种,则组成的两位数恰好是3的倍数的概率是: . 学生熟练运用本节树状图或列表法求概率步骤,互相补充,教师订正答案,最后总结本节内容。 练习是为了巩固学生所学的新知,教会学生运用树状图法或列表法求概率的步骤来解决问题。
课堂小结 学生先发言总结本节用树状图法或列表法求概率的步骤,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:26.2.2等可能情形下的简单概率计算1.树状图法2.列表法
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
