【新课标】26.2.2用列表或画树状图形等可能情形下的概率 课件(共38张PPT)
文档属性
| 名称 | 【新课标】26.2.2用列表或画树状图形等可能情形下的概率 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 16:07:51 | ||
图片预览










文档简介
(共38张PPT)
26.2.2用列表或画树状图形
等可能情形下的概率
沪科版 九年级下
教学内容分析
在上节学习了求简单概率的基础上,进一步学习了计算概率方法,能够进行简单的概率计算;掌握用树状图法或者列举法求概率的方法,熟练运用树状图解决实际问题。
教学目标
1.在求简单事件概率基础上,进一步学习计算概率的方法,能够进行简单的概率计算;(重点)
2.掌握用树状图法或列表法求概率的方法,熟练运用树状图或列表法解决实际问题。(难点)
核心素养分析
本节利用树状图法或列表法求比较复杂事件的概率,总结了树状图法或列表法求概率的步骤,培养了学生随机性的认识,发展了学生应用概率知识的意识。
新知导入
概率的性质有哪些?
当A是必然事件时,P(A)=1;
当A是不可能事件时,P(A)=0。
所以有0≤P(A)≤1.
一般地,对任何随机事件A,它的概率P(A)满足0必然事件的概率为1,不可能事件的概率为0.
新知讲解
例2 同时抛掷2枚均匀的硬币一次,求2枚硬币都是正面向上的概率.
解 同时抛掷2枚硬币一次,可能出现如下4种不同的结果:
(正,正),(正,反),(反,正),(反,反).
新知讲解
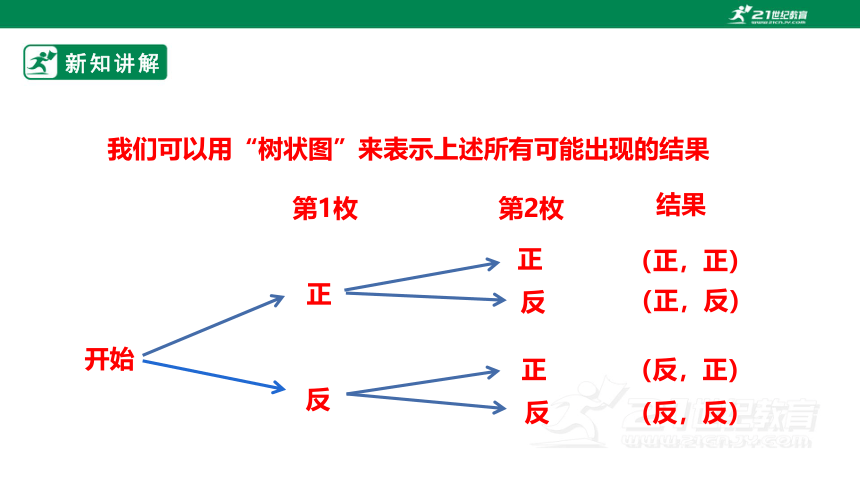
第1枚
第2枚
结果
开始
正
反
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
我们可以用“树状图”来表示上述所有可能出现的结果
新知讲解
2枚硬币都是正面向上的的概率多少
解:每种结果出现的可能性相等,
其中2枚硬币都是正面向上的结果只有(正,正)这1种,
设2枚硬币都是正面向上的事件为A,
则事件A的概率为 P(A)=
新知讲解
新知讲解
1枚出现正面1枚出现反面的概率多少
新知讲解
例3 某班有1名男生,2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各选1名去领奖,求2名领奖学生都是女生的概率.
新知讲解
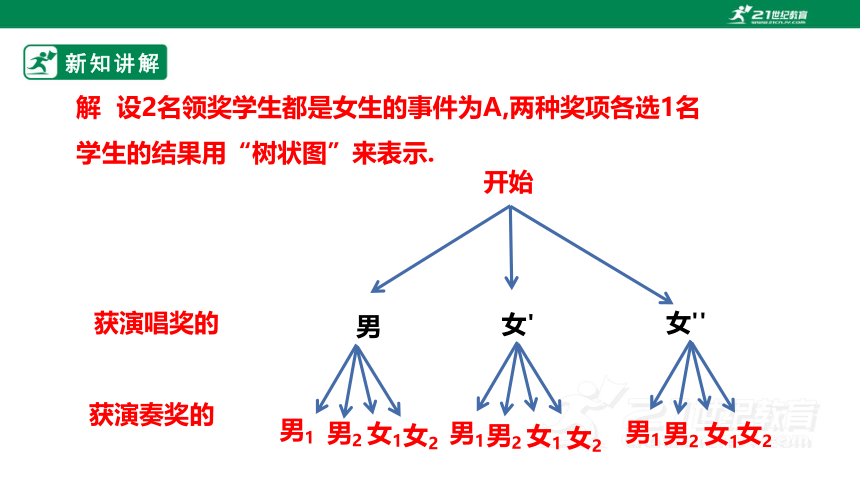
获演唱奖的
获演奏奖的
开始
男
女''
女'
男1
男2
女1
女2
男1
男2
女1
女2
男1
男2
女1
女2
解 设2名领奖学生都是女生的事件为A,两种奖项各选1名学生的结果用“树状图”来表示.
新知讲解
由于共有12种结果,且每种结果出现的可能性相等,
其中2名领奖学生都是女生的结果有4种,
所以事件A发生的概率为
P(A)=
新知讲解
计算等可能情形下概率的关键是确定所有可能性相等的结果总数n和求出其中使事件A发生的结果总数m.“树状图”能帮助我们有序地思考,不重复、不遗漏地得出n和m.
新知讲解
变式:一个不透明的袋中装有18个红球和若干个白球,它们除颜色外其他均相同.
已知将袋中球摇匀后,从中任意摸出一个球是红球的概率是 。
求袋中总共有多少个球
解:设袋中有x个球,
∵袋中装有18个红球,从中任意摸出一个球是红球的概率是
∴
解得:x =30
即袋中总共有30个球.
新知讲解
新知讲解
画树形图求概率的基本步骤
(1)确定一次试验的步骤;
(2)画树状图列举一次试验的所有等可能结果;
(3)确定随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式计算.
新知讲解
例4 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1 ,2,…,6。试分别计算如下各随机事件的概率:
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12。
新知讲解
分析:为了解决这个问题,我们首先要弄清楚一共有多少个可能结果。虽然同时抛掷2枚均匀的骰子一次,点数之和可能为2,3 ,…,12中的任何一种,但是它们并不是发生的所有可能结果。所有可能结果有哪些呢
新知讲解
我们知道:
第1枚骰子可能掷出1,2,…,6 中的每一种情况,
第2枚骰子也可能掷出1,2,…,6中的每一种情况,
而且无论第1枚骰子掷出1,2,…,6中的哪一种情况,
第2枚骰子都可能掷出1,2,…,6中的任一种情况。
新知讲解
所以我们用“列表法”列出所有的可能结果如下:
新知讲解
解 从上面表格中可以看出,同时抛掷2枚骰子一次,所有可能出现的结果有36种。
由于骰子是均匀的,所以每个结果出现的可能性相等。
(1)抛出的点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8这个事件发生的概率为 ;
(2)抛出的点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12这个事件发生的概率为 。
新知讲解
从这个例子中再次体会弄清楚所有可能结果的重要性.
如同“树状图”一样,“列表法”也能帮助我们有序地思考。
当一个试验有两个相关因素,且所有可能的结果较多时,为不重不漏地列出所有可能的结果,通常采用列表法
新知讲解
用列表法求概率步骤:
1.列表;
2.通过表格计数;
3.利用概率公式计算出事件的概率.
1.不透明的布袋中有红、黄、蓝3种颜色不同的小球各1个,它们除颜色不同外其余完全相同,先从中随机摸出1个,记录下它的颜色,将它放回布袋并搅匀,再从中随机摸出1个,记录下颜色,那么这两次摸出小球的颜色都为蓝色的概率是__________.
课堂练习
解:树状图如图所示:
共有9种等可能情况,其中两次摸出小球的颜色都为蓝色有1种,
∴这两次摸出小球的颜色都为蓝色的概率是 .
课堂练习
课堂练习
2.在4件同型号的产品A,B,C,D中,A ,B,C为合格产品,D为不合格产品.
(1)从这4件产品中随机抽取1件进行检测,直接写出抽到合格品的概率;
(2)从这4件产品中任抽取一件检测后放回,再抽取一件进行检测,请用画树状图法或列表法求两次抽到的都是合格品的概率.
课堂练习
解:(1)∵4件同型号的产品A,B,C,D中,A,B,C为合格产品,D为不合格产品,
∴合格品的概率为:P= .
(2)如树状图下图:
P=
课堂练习
3.将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
课堂练习
(1)从中随机抽出一张牌,牌面数字小于3的概率是______;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是3的倍数的概率.
课堂练习
解:(1)四张牌中任抽取一张,所有等可能的结果有4种,
其中牌面数字小于3的结果有2种,
则从中随机抽出一张牌,
牌面数字小于3的概率是 ;
课堂练习
(2)解:列表如下:
课堂练习
由表知,所有可能的结果数有16种,
其中组成的两位数是3的倍数的有5种,
则组成的两位数恰好是3的倍数的概率是: .
课堂总结
画树状图法
画树状图和列表法求概率
列表法
如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法。
当一个试验有两个相关因素,且所有可能的结果较多时,为不重不漏地列出所有可能的结果。
板书设计
26.2.2等可能情形下的简单概率计算
1.树状图法
2.列表法
作业布置
必做题:课本习题P99的第2~3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
26.2.2用列表或画树状图形
等可能情形下的概率
沪科版 九年级下
教学内容分析
在上节学习了求简单概率的基础上,进一步学习了计算概率方法,能够进行简单的概率计算;掌握用树状图法或者列举法求概率的方法,熟练运用树状图解决实际问题。
教学目标
1.在求简单事件概率基础上,进一步学习计算概率的方法,能够进行简单的概率计算;(重点)
2.掌握用树状图法或列表法求概率的方法,熟练运用树状图或列表法解决实际问题。(难点)
核心素养分析
本节利用树状图法或列表法求比较复杂事件的概率,总结了树状图法或列表法求概率的步骤,培养了学生随机性的认识,发展了学生应用概率知识的意识。
新知导入
概率的性质有哪些?
当A是必然事件时,P(A)=1;
当A是不可能事件时,P(A)=0。
所以有0≤P(A)≤1.
一般地,对任何随机事件A,它的概率P(A)满足0
新知讲解
例2 同时抛掷2枚均匀的硬币一次,求2枚硬币都是正面向上的概率.
解 同时抛掷2枚硬币一次,可能出现如下4种不同的结果:
(正,正),(正,反),(反,正),(反,反).
新知讲解
第1枚
第2枚
结果
开始
正
反
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
我们可以用“树状图”来表示上述所有可能出现的结果
新知讲解
2枚硬币都是正面向上的的概率多少
解:每种结果出现的可能性相等,
其中2枚硬币都是正面向上的结果只有(正,正)这1种,
设2枚硬币都是正面向上的事件为A,
则事件A的概率为 P(A)=
新知讲解
新知讲解
1枚出现正面1枚出现反面的概率多少
新知讲解
例3 某班有1名男生,2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各选1名去领奖,求2名领奖学生都是女生的概率.
新知讲解
获演唱奖的
获演奏奖的
开始
男
女''
女'
男1
男2
女1
女2
男1
男2
女1
女2
男1
男2
女1
女2
解 设2名领奖学生都是女生的事件为A,两种奖项各选1名学生的结果用“树状图”来表示.
新知讲解
由于共有12种结果,且每种结果出现的可能性相等,
其中2名领奖学生都是女生的结果有4种,
所以事件A发生的概率为
P(A)=
新知讲解
计算等可能情形下概率的关键是确定所有可能性相等的结果总数n和求出其中使事件A发生的结果总数m.“树状图”能帮助我们有序地思考,不重复、不遗漏地得出n和m.
新知讲解
变式:一个不透明的袋中装有18个红球和若干个白球,它们除颜色外其他均相同.
已知将袋中球摇匀后,从中任意摸出一个球是红球的概率是 。
求袋中总共有多少个球
解:设袋中有x个球,
∵袋中装有18个红球,从中任意摸出一个球是红球的概率是
∴
解得:x =30
即袋中总共有30个球.
新知讲解
新知讲解
画树形图求概率的基本步骤
(1)确定一次试验的步骤;
(2)画树状图列举一次试验的所有等可能结果;
(3)确定随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式计算.
新知讲解
例4 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1 ,2,…,6。试分别计算如下各随机事件的概率:
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12。
新知讲解
分析:为了解决这个问题,我们首先要弄清楚一共有多少个可能结果。虽然同时抛掷2枚均匀的骰子一次,点数之和可能为2,3 ,…,12中的任何一种,但是它们并不是发生的所有可能结果。所有可能结果有哪些呢
新知讲解
我们知道:
第1枚骰子可能掷出1,2,…,6 中的每一种情况,
第2枚骰子也可能掷出1,2,…,6中的每一种情况,
而且无论第1枚骰子掷出1,2,…,6中的哪一种情况,
第2枚骰子都可能掷出1,2,…,6中的任一种情况。
新知讲解
所以我们用“列表法”列出所有的可能结果如下:
新知讲解
解 从上面表格中可以看出,同时抛掷2枚骰子一次,所有可能出现的结果有36种。
由于骰子是均匀的,所以每个结果出现的可能性相等。
(1)抛出的点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8这个事件发生的概率为 ;
(2)抛出的点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12这个事件发生的概率为 。
新知讲解
从这个例子中再次体会弄清楚所有可能结果的重要性.
如同“树状图”一样,“列表法”也能帮助我们有序地思考。
当一个试验有两个相关因素,且所有可能的结果较多时,为不重不漏地列出所有可能的结果,通常采用列表法
新知讲解
用列表法求概率步骤:
1.列表;
2.通过表格计数;
3.利用概率公式计算出事件的概率.
1.不透明的布袋中有红、黄、蓝3种颜色不同的小球各1个,它们除颜色不同外其余完全相同,先从中随机摸出1个,记录下它的颜色,将它放回布袋并搅匀,再从中随机摸出1个,记录下颜色,那么这两次摸出小球的颜色都为蓝色的概率是__________.
课堂练习
解:树状图如图所示:
共有9种等可能情况,其中两次摸出小球的颜色都为蓝色有1种,
∴这两次摸出小球的颜色都为蓝色的概率是 .
课堂练习
课堂练习
2.在4件同型号的产品A,B,C,D中,A ,B,C为合格产品,D为不合格产品.
(1)从这4件产品中随机抽取1件进行检测,直接写出抽到合格品的概率;
(2)从这4件产品中任抽取一件检测后放回,再抽取一件进行检测,请用画树状图法或列表法求两次抽到的都是合格品的概率.
课堂练习
解:(1)∵4件同型号的产品A,B,C,D中,A,B,C为合格产品,D为不合格产品,
∴合格品的概率为:P= .
(2)如树状图下图:
P=
课堂练习
3.将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
课堂练习
(1)从中随机抽出一张牌,牌面数字小于3的概率是______;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是3的倍数的概率.
课堂练习
解:(1)四张牌中任抽取一张,所有等可能的结果有4种,
其中牌面数字小于3的结果有2种,
则从中随机抽出一张牌,
牌面数字小于3的概率是 ;
课堂练习
(2)解:列表如下:
课堂练习
由表知,所有可能的结果数有16种,
其中组成的两位数是3的倍数的有5种,
则组成的两位数恰好是3的倍数的概率是: .
课堂总结
画树状图法
画树状图和列表法求概率
列表法
如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法。
当一个试验有两个相关因素,且所有可能的结果较多时,为不重不漏地列出所有可能的结果。
板书设计
26.2.2等可能情形下的简单概率计算
1.树状图法
2.列表法
作业布置
必做题:课本习题P99的第2~3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
