青岛版数学五年级下册 七 包装盒——长方体和正方体 课件(共260张PPT)
文档属性
| 名称 | 青岛版数学五年级下册 七 包装盒——长方体和正方体 课件(共260张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 52.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 11:16:34 | ||
图片预览








文档简介
(共260张PPT)
七 包装盒
——长方体和正方体
长方体和正方体的认识
情境导入
从图中,你能知道哪些数学信息?
这些图形都是立体图形。
这些图形都是立体图形。
根据这些信息,你能提出什么问题?
长方体有哪些特征?
正方体有哪些特征?
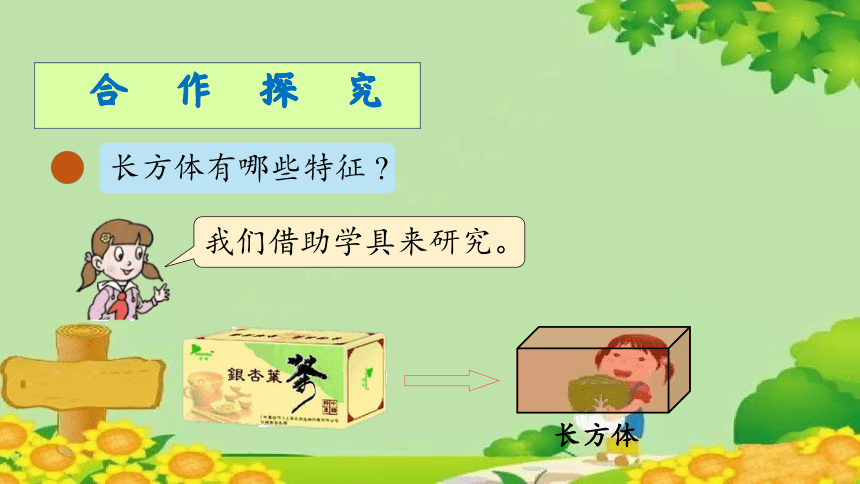
合作探究
长方体有哪些特征
我们借助学具来研究。
长方体
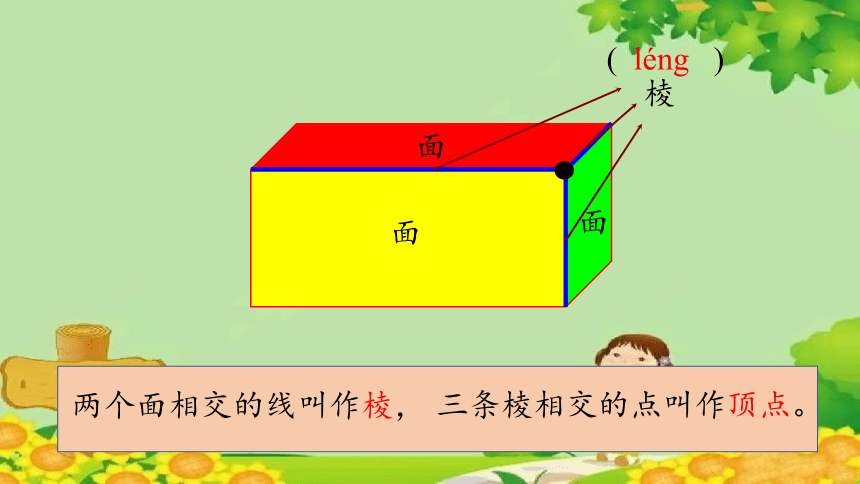
面
面
面
两个面相交的线叫作棱,
( léng )
棱
三条棱相交的点叫作顶点。
我发现长方体有6个面,它们是长方形(有时有两个相对的面是正方形),相对的面……
长方体有8个顶点。
长方体有12条棱,按长度可以分成3组,相对的4条棱……
长方体有6个面,都是长方形(可能有两个相对的面是正方形)。
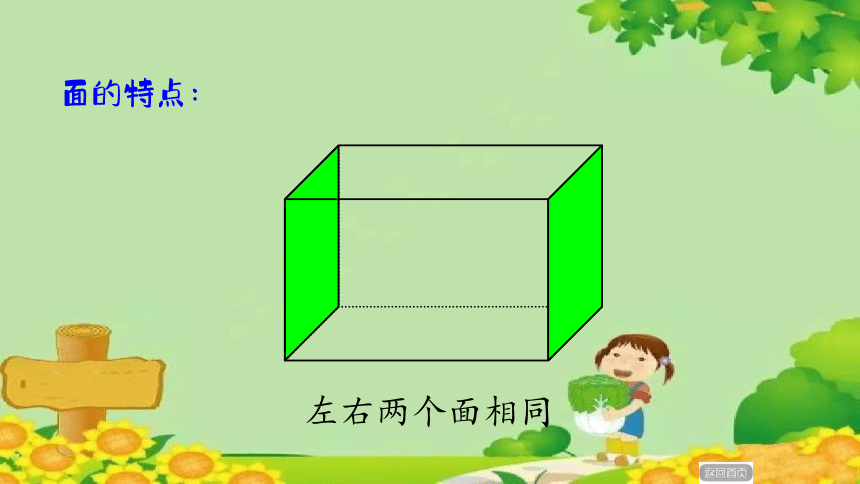
面的特点:
上下两个面相同
面的特点:
左右两个面相同
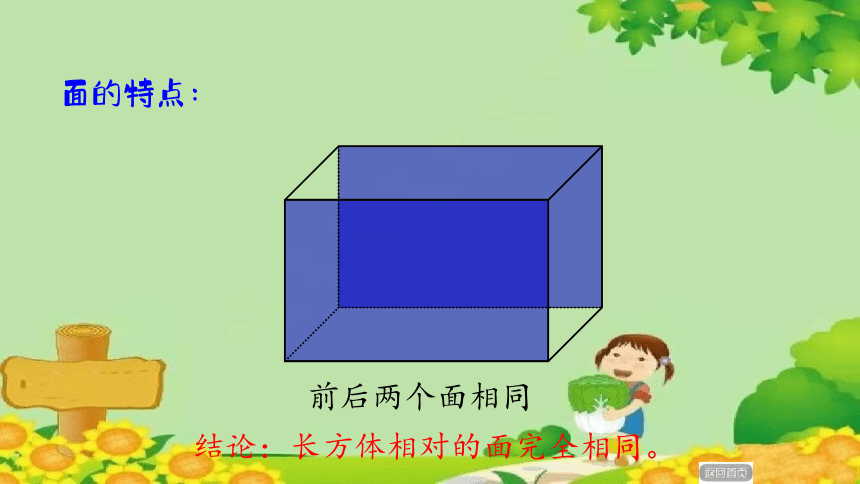
面的特点:
结论:长方体相对的面完全相同。
前后两个面相同
面的特点:
长方体共有12条棱。
棱的特点:
长方体有12条棱,可以分成3组,相对的4条棱的长度相等。
棱的特点:
长方体共有8个顶点。
顶点的特点:
从一个方向观察一个长方体,最多能同时看到几个面?
从一个方向观察一个长方体,最多能同时看到3个面。
长
宽
高
相交于一个顶点的三条棱的长度,分别叫作长方体的长、宽、高。
试一试
(选题源于《亲子作业本》)
看图回答问题。
(1) 这个纸巾盒的前面是什么形状?长和宽各是多少?和它相同的面是哪个?
前面是长方形。
长:24cm、宽9cm。
后面
(选题源于《亲子作业本》)
(2) 它的右面是什么形状?长和宽各是多少?和它相同的面是哪个?
右面是长方形。
长:12cm、宽9cm。
左面
(选题源于《亲子作业本》)
(3) 哪几个面的长是24cm,宽是12cm
上面和下面
正方体有哪些特征
我们借助学具来研究一下吧 !
正方体有 6个面它们是完全相同的正方形。
正方体有8个顶点12 条棱,每条棱的长度都相等。
上下两个面相同
面的特点:
左右两个面相同
面的特点:
6个面是完全相同的正方形
前后两个面相同
面的特点:
正方体有12条棱,所有的棱长度相等。
棱的特点:
顶点的特点:
正方体共有8个顶点。
正方体与长方体有什么联系与区别
正方形是特殊的长方形,正方体是不是特殊的长方体呢
我们整理一下吧。
面 棱 顶点
长方体
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
相对的4条棱长度相等(可能有8条棱长度相等)
8个
面 棱 顶点
正方体
6个面都是
正方形,6
个面完全相同。
12条棱长
度相等
8个
正方体是特殊的长方体。可以用右图表示正方体和长方体的关系。
长方体
正方体
试一试
(选题源于《亲子作业本》)
1. 填空。
(1) 相交于一个顶点的三条棱的长度,分别叫作长方体的( )、( )、( )。
长
宽
高
(选题源于《亲子作业本》)
(2) 看图,写一写长方体的长、宽、高各是多少。
5 cm
2 cm
5 cm
长( )cm
宽( )cm
高( )cm
5
2
5
(选题源于《亲子作业本》)
12 cm
7 cm
4 cm
长( )cm
宽( )cm
高( )cm
12
7
4
(3) 请把正方体和长方体的名称填入下图中。
(选题源于《亲子作业本》)
( )
( )
长方体
正方体
(选题源于《亲子作业本》)
(4)长方体有( )个面,( )条棱,( )个顶点,相对的两个面( ),相对的棱的长度( )。
(5) 正方体有( )个面,( )条棱,( )个顶点,所有的面都( ),所有棱的长度都( )。
(6)长方体的面都是( )形,特殊的长方体有两个相对的面是( )形,此时其余四个面的面积( )。
6
12
8
完全相同
相等
6
12
8
相同
相等
长方
正方
相等
自主练习
第84页*自主练习*第1题
1. 说一说。
(1) .墨汁盒的上面是什么形状 与它
相对的是哪个面
墨汁盒的上面是长方形;与它相对的面是下面。
第84页*自主练习*第1题
(2) 前面的长和宽各是多少 哪个面
与它相同
前面的长是12厘米,宽是5厘米;后面与它相同。
第84页*自主练习*第1题
(3) 哪个面的长是12厘米,宽是3厘米
左、右两个面的长是12厘米,宽是3厘米。
第84页*自主练习*第2题
2. 说出每个长方体的长、宽、高各是多少。
长:7cm
宽:5cm
高:6cm
第84页*自主练习*第2题
长:3 dm
宽:2 dm
高:4 dm
第84页*自主练习*第2题
长:2 m
宽:0.5 m
高:0.5 m
第84页*自主练习*第3题
3. 观察右图,回答问题。
(1) 两个储物箱的形状都是正方体吗
不都是,第一个储物箱的形状是正方体,第二个储物箱的形状是长方体。
第84页*自主练习*第3题
(2) 正方体储物箱的棱长是多少 哪几个面完全相同
棱长是6分米,6个面完全相同。
第84页*自主练习*第3题
(3) 长方体储物箱的长、宽、高各是多少 哪几个面完全相同
长是7分米,宽是6分米,高是6分米。上、下、左、右4个面完全相同,前、后2个面完全相同。
第84页*自主练习*第4题
4. 量一量。
以其中一种物品为例,说一说每个面的长和宽各是多少。
提示:根据测量所得的数据填表并回答问题。
第85页*自主练习*第5题
5. 哪几个面可以围成一个长方体
①号、②号、③号、⑤号、⑥号和⑦号6个面可以围成一个长方体。
第85页*自主练习*第6题
6. 计算下图中长方体和正方体每个面的面积。
前、后面:13×5=65 (平方厘米)
上、下面:13×2=26 (平方厘米)
左、右面:5×2=10 (平平方厘米)
第85页*自主练习*第6题
每个面的面积:
8×8=64 (平方米)
第85页*自主练习*第6题
前、后面:18×5=90(平方分米)
上、下面:5×2=10(平方分米)
左、右面:18×2=36(平方分米)
第85页*自主练习*第7题
7. 用12个棱长是1厘米的小正方体拼成一个长方体,有几种不同的拼法 拼成的长方体的长、宽、高各是多少
有4种不同的拼法,每种拼法的长、宽、高分别是12厘米、1厘米、1厘米;6厘米、2厘米、1厘米;4厘米、3厘米、1厘米;3厘米、2厘米、2厘米。
(摆放方式不同,对应的长、宽、高就不同)
第85页*自主练习*第8题
一个长方体广告灯箱长5米,宽0.5米,高3米。灯箱的框架用铝条镶嵌,至少需要多少米铝条
8 .
(5+0.5+3) ×4=34 (米)
方形西瓜
你见过方形西瓜吗 你知道它们是怎样长成的吗
瓜农们将幼瓜置于按一定规格做好的长方体形状的透明玻璃模具里,幼瓜最终就长成了方形西瓜。
这种瓜不仅为运输储藏带来
方便,还会因外形奇特而更加
吸引消费者。
你知道了吗?
长方体和正方体的表面积
情景导入
从图中,你能知道哪些数学信息?
根据这些信息,你能提出什么问题?
制作这样一个电脑包装箱至少需要多少平方厘米纸板?
做一个化妆品盒子至少需要多少平方厘米纸板?
合作探究
制作这样一个电脑包装箱至少需要多少平方厘米纸板
要求需要多少平方厘米纸板就是求电脑包装箱6个面的总面积。
怎样求长方体6个面的总面积呢?
我们借助长方体表面的展开图来研究吧。
将一个长方体的表面展开:
上
上
下
前
后
上
下
前
后
左
上
下
前
后
左
右
上
下
前
后
左
右
下
前
后
上
左
右
上
下
前
后
左
右
上
前
右
你能在展开图上找到其他的3个面吗 哪些面的面积相等
分别求出相对面的面积,再相加。
前、后面:50×30×2=
左、右面:20×30×2=
上、下面:50×20×2=
总面积:_______________________________________
3000 (平方厘米)
1200 (平方厘米)
2000 (平方厘米)
3000 +1200 +2000 =6200 (平方厘米)
先求前面、右面、上面3个面的面积之和,再乘2。
(50×30+20×30+50×20)×2
=__________________________
=__________________________
答:制作这样一个电脑包装箱至少需要_________平方厘米纸板。
(1500 + 600 + 1000)×2
3100×2
= 6200 (平方厘米)
6200
根据刚才的解题过程,你能总结出长方体的表面积计算公式吗?
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2
长方体的表面积 = (长×宽+长×高+宽×高)×2
长方体的表面积计算公式。
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2
长方体的表面积 = (长×宽+长×高+宽×高)×2
试一试
(选题源于《亲子作业本》)
计算下面图形的表面积。
2 m
0.5 m
0.5 m
(1)
2×0.5×4+0.5×0.5×2
= 4+0.5
= 4.5(m2)
(选题源于《亲子作业本》)
8 m
7 m
5 m
(2)
(5×8+5×7+7×8)×2
=131×2
=262(m2)
做一个化妆品盒子至少需要多少平方厘米纸板
求做一个化妆品盒子至少需要多少平方厘米纸板,实际就是求······
求正方体6个面的总面积。
怎样求正方体6个面的总面积呢?
正方体的6个面是完全相同的正方形,只要先求出一个面的面积,再乘6即可。
5×5×6
=_____________
=_____________
25×6
150(平方里面)
答:做一个化妆品盒子至少需要_____平方厘米纸板。
150
你能总结出正方体的表面积计算公式吗?
正方体的表面积=棱长×棱长×6
长方体或正方体6个面的总面积,叫作它的表面积。
试一试
(选题源于《亲子作业本》)
1. 计算下面图形的表面积。
4 m
4 m
4 m
4×4×6
= 16×6
= 96 (m2)
(选题源于《亲子作业本》)
2. 一个塑料板制成的文具盒,长是2.2分米,宽是8厘米,高是2厘米,它需要多少平方厘米的塑料板?制作6个这样的文具盒需要塑料板多少平方厘米?
2.2分米=22厘米
(22×8+22×2+8×2)×2=472(平方厘米)
472×6=2832(平方厘米)
(选题源于《亲子作业本》)
3. 下面是一个长方体的展开图,求该长方体的表面积。
(单位:厘米)
(8×6+8×2+6×2)×2=152 (平方厘米)
自主练习
第88页*自主练习*第1题
1.下面的平面图哪些可以折成长方体或正方体
图①、图③可以折成长方体,图④可以折成正方体。
第88页*自主练习*第2题
2. 右图是一个长方体。
(1) 上面的面积是_______平方厘米。
(2) 前面的面积是_______平方厘米。
(3) 右面的面积是_______平方厘米。
(4) 表面积是________平方厘米。
24
30
20
148
第88页*自主练习*第3题
3. 右图是一个长方体。
(3×2 +3×1+2×1)×2 = 22(dm2)
第88页*自主练习*第3题
5×5×6=150(cm2)
第88页*自主练习*第3题
(0.4×0.4 +0.4×0.7+0.4×0.7)×2 = 1.44 (m2)
第88页*自主练习*第4题
4. 包装形如右图的正方体礼盒,至少需要多少平方分米的包装纸
12×12×6=864 (平方厘米)
864平方厘米=8.64平方分米
第88页*自主练习*第5题
做这样一个手提袋至少需要多少平方厘米的纸板
5 . (1)
30×40×2+30×10+10+40×2=3500 (平方厘米)
第89页*自主练习*第5题
鱼缸的4个侧面是用玻璃做的。做这样一个鱼缸至少需要多少平方厘米的玻璃
(2)
(60×80+160×80)×2=35200 (平方厘米)
第89页*自主练习*第6题
6. 方形雨水管横截面的长是10厘米,宽是8厘米。每一节雨水管长2米。做25节这样的雨水管至少需要多少平方米铁皮
10厘米=0.1米
8厘米=0.08米
(0.1×2 + 0.08×2)×2×25 = 18 (平方米)
第89页*自主练习*第7题
7.一间教室长9米,宽7米,高3米。要粉刷教室的屋顶和四面墙壁 ( 除去门窗和黑板的面积29.6平方米),粉刷面积是多少平方米 如果平均每平方米用0.2千克涂料,至少需要多少千克涂料
9×7+9×3×2+7×3×2-29.6 =129.4(平方米)
0.2×129.4 = 25.88 (千克)
第89页*自主练习*第8题
8. (1) 量一量《新华字典》的长、宽、高分别是多少,然后算出它的表面积。
提示:先用尺子测量出《新华字典》的长、宽、高,再算出它的表面积,最后用纸把2本《新华字典》包起来,看一看有几种包法,哪种包法最省纸。
(2) 如果用纸把2本《新华字典》包起来,有几种包法 哪种包法最省纸
聪明小屋
(1) 2个棱长1厘米的正方体,它们的表面积总和是多
少平方厘米 把它们拼成一个长方体后,表面积减
少了多少平方厘米
1×1×6×2=12 (平方厘米)
1×1×2=2 (平方厘米)
聪明小屋
(2) 3个这样的正方体拼成一个长方体后,表面积减少
了多少平方厘米 4个呢
1×1×4=4 (平方厘米)
1×1×6=6 (平方厘米)
聪明小屋
(3) 你有什么发现
发现:每增加一个正方体,拼成的长方体的表面积就比正方体的表面积总和少2个正方形的面积,即按这样的拼法,n个棱长1厘米的正方体拼成一个长方体后,减少的表面积为[1×1×2×(n-1)]平方厘米。
聪明小屋
(4) 按这样的拼法,20个小正方体拼成一个长方体后,
表面积减少了多少平方厘米
1×1×2× (20-1) =38 (平方厘米)
体积、溶积及单位间的进率
情景导入
从图中,你知道了哪些数学信息?
体积:50×50×20
体积:40×30×20
体积:50×50×20
体积:40×30×20
根据这些信息,你能提出什么问题?
什么是体积?
合作探究
什么是体积?
我们做个实验吧。
实验一要求
2. 用手提绳子将石头浸入玻璃杯的水中,观察放入石
头后水位有的变化情况。
3. 说说观察的结果,想一想,这说明了什么?
1. 准备盛有半杯红色水的玻璃杯和用绳子捆着的石
头一块。
1. 准备2个同样的杯子。第一个杯子装满沙子,第二
个杯子空杯。
2. 将一块木块放入第二个杯子中,然后从第一个杯
子向第二个杯子中倒沙子,倒满为止。
3. 说说观察的结果,想一想,这说明了什么?
实验二要求
将石块放入水中
石块占了水槽的空间
实验一:
水面上升
我发现水槽里的水面升高了。因为······
实验二:
将木块放入空杯中
木块占了空杯的空间
我发现······
物体所占空间的大小叫作物体的体积。
空气 、橙汁、冰箱都占空间。
你能说说生活中哪些物体占空间吗?
下面的长方体和正方体,谁的体积大?
大小不明显,看不出来,需要计量。
用什么计量比较合适呢?
我知道用 能计量出长方形、正方形的面积。
15个
16个
我猜想可以用 计量体积。
24个
27个
体积单位可以写成:
面积单位有平方厘米、平方分米······体积单位有哪些呢
常用的面积单位有:平方厘米 平方分米 平方米
常用的体积单位有:
立方厘米
立方分米
cm3
dm3
m3
立方米
试一试
(选题源于《亲子作业本》)
1. 填空。
(1) 物体所占( )的大小叫作物体的体积。
(2) 把冰箱、文具盒和微波炉进行比较,( ) 的体积最大,( ) 的体积最小。
(3) 棱长是1cm、1dm和1m的正方体的体积分别是1( )、1( )和1( )。
空间
冰箱
文具盒
cm3
dm3
m3
(选题源于《亲子作业本》)
2. 选择。
(1) 体积单位和面积单位相比较,( )。
A.体积单位大 B.面积单位大 C.无法比较
(2) 有两个棱长都是1分米的正方体,一个是木块,另一个是铁块。它们的体积相比,( )大。
A.铁块 B.木块 C.同样
C
C
棱长为1厘米的正方体,体积是1立方厘米。
1cm
1cm
1cm
1立方厘米有多大呢?
一个手指尖的体积大约是1立方厘米。
一粒花生米的体积大约是1立方厘米。
生活中哪些物体的体积大约是1立方厘米?
牛奶箱的体积用立方厘米作单位来测量合适吗?
1立方厘米太小,用1立方分米作单位比较合适。
1cm
1cm
1cm
1dm
1dm
1dm
棱长为1分米的正方体,体积是1立方分米。
1立方分米有多大呢?
棱长为1分米的正方体,体积是1立方分米。
粉笔盒的体积大约是1立方分米。
集装箱的体积用立方分米作单位来测量合适吗?
1立方分米太小,用1立方米作单位比较合适。
1dm
1dm
1dm
1m
1m
1m
棱长为1米的正方体,体积是1立方米。
1立方米有多大呢?
说一说,生活中哪些物体的体积大约是1立方米?
棱长为1米的正方体,体积是1立方米。
装29英寸电视机的纸箱的体积大约是1立方米。
想一想,在体积单位的探索过程中,我们运用了什么方法?
类比
平方厘米
平方分米
平方米
常用的面积单位
类 比
立方厘米
立方分米
立方米
常用的面积单位
1. 判断。
(1) 把一块正方体铁块铸成一块长方体,体积不变。
( )
(2) 棱长是1米的正方体,它的体积一定是1立方米。
( )
(3) 一个烟盒的体积大约是96立方分米。( )
试一试
(选题源于《亲子作业本》)
2.下面的图形都是用棱长为1cm的小正方体摆成的,写出
它们的体积。
( ) cm3
( ) cm3
( ) cm3
(选题源于《亲子作业本》)
9
6
13
( ) cm3
( ) cm3
( ) cm3
(选题源于《亲子作业本》)
7
6
10
(选题源于《亲子作业本》)
3. 在括号里填上合适的单位。
文具盒的体积约是200( )。 西瓜的体积约是15( )。
手机的体积约是70( )。 冰箱的体积约是1.2( )。
cm3
dm3
cm3
m3
牙膏盒的体积约是120( )。
生日蛋糕的体积约是16( )。
(选题源于《亲子作业本》)
cm3
dm3
想一想,用棱长1厘米的小正方体摆成下面的长方体和正方体,它们的体积各是多少
计量一个物体的体积,要看这个物体含有多少个“体积单位”。
1立方分米是多少立方厘米呢
我用1立方厘米的方木块摆。
一行摆10个,一层摆10行,摆10层,我发现······
1立方分米=1000立方厘米
1立方米=1000立方分米
在括号里填上合适的数。
2.25 m3= ( ) dm3 760 cm3= ( ) dm3
76000 cm3= ( ) dm3= ( ) m3
0.8 dm3= ( ) cm3
7.56 m3= ( ) dm3= ( ) cm3
(选题源于《亲子作业本》)
试一试
2250
0.76
76
0.076
800
7560
7560000
哪个奶盒装的牛奶多一些
哪个盒内的空间大,哪个就装得多。
哪个盒内的空间大,哪个就装得多。
用同样的杯子量一量······
红色牛奶盒装的牛奶多。
容器所能容纳物体的体积,叫作它们的容积。
计量容积一般用体积单位。但是计量液体的体积,如水、油等,常用容积单位升与毫升。升与毫升可以分别写成L和mL。
10mL
500mL
1L
你知道计量容积的单位有哪些吗?
1升 =1立方分米
1升 = 1000毫升
1毫升 =1立方厘米
(选题源于《亲子作业本》)
试一试
1. 填空。
(1) 物体所占( )叫作物体的体积,容器( )叫作容器的容积。
(2) 课桌的体积比书本的体积( )。
空间的大小
所能容纳物体的体积
大
(3) 在括号里填上合适的单位名称。
① 一个油桶能装油5( )。
② 一盒纯牛奶大约是250( )。
③集装箱的容积大约是40( )。
④ 一个长方体游泳池的容积大约是800( )。
(选题源于《亲子作业本》)
L
mL
m3
m3
(选题源于《亲子作业本》)
2. 判断。
(1) 两个物体相比较,容积大的物体体积也比较大。
( )
(2) 物体一定有体积,但不一定有容积。( )
(3) 一个木盒和一个纸盒的体积相等,它们的容积也相等。( )
(选题源于《亲子作业本》)
3. 选择。
(1) 一个玻璃瓶可装350毫升的饮料,这个瓶子的( )是350毫升。瓶子占地32平方厘米,是指瓶子的( )。
A.底面积 B.体积 C.容积
(2) 物体的体积和容积的根本区别是( )不同。
A.计量单位 B.意义 C.计算方法
C
A
B
(3) 一瓶牛奶,牛奶的体积就是瓶子的( )。
A.容积 B.体积 C.质量
(选题源于《亲子作业本》)
A
(选题源于《亲子作业本》)
4. 单位换算。
5m3= ( )dm3 530cm3 =( )dm3
2.3m3 =( )dm3 =( )L
9L 62mL =( )L
7.8L = ( )dm3 =( )mL
2.6dm3 =( )L =( )cm3
5000
0.53
2300
2300
9.062
7.8
7.8
2.6
2600
自主练习
1. 说一说谁的体积大。
第93页*自主练习*第1题
第93页*自主练习*第2题
2. 下面的图形都是用棱长1厘米的小正方体摆成的,说
一说它们的体积各是多少立方厘米。
8立方厘米
7立方厘米
7立方厘米
第94页*自主练习*第3题
3. 填上合适的单位名称。
墨水瓶的容积约是60( )。
微波炉的体积约是40( )。
毫升
立方分米
第94页*自主练习*第3题
酸奶盒的容积约是240( )。
矿泉水桶的容积约是20( )。
毫升
升
第94页*自主练习*第3题
集装箱的体积约是50( )。
文具盒的体积约是200( )。
立方米
立方厘米
第94页*自主练习*第4题
4 .
3.03dm3= ( )L
800cm3= ( )dm3
320mL= ( )L
0.5m3= ( )dm3
4526mL= ( )cm3
2340L= ( ) m3
3.03
500
0.8
4526
0.32
2.34
第94页*自主练习*第5题
5. 整理并填表。
常用单位名称 相邻两个单位间的进率
长度单位
面积单位
体积单位
米、分米、厘米
10
平方米、平方分米、平方厘米
100
立方米、立方分米、立方厘米
1000
第94页*自主练习*第6题
6. 估一估,填一填。
5升
( )升
2000毫升
( ) 毫升
2.5
700
第94页*自主练习*第7题
7.一瓶矿泉水有500mL,纸杯的容积约是120mL。
(1) 一瓶矿泉水大约能倒满几杯
(2) 一个人平均每天大约需要喝1300毫升的水,如果
使用这样的纸杯,每天大约需要喝多少杯水
(1) 大约能倒满4杯。
(2) 每天大约需要喝11杯水。
长方体和正方体体积
情景导入
从图中,你知道了哪些数学信息?
可乐箱的长、宽、高分别是7dm、3dm、2dm。
桃汁饮料盒的长、宽、高分别是10cm、7cm、20cm。
啤酒箱的长、宽、高分别是3dm、3dm、3dm。
可乐箱的长、宽、高分别是7dm、3dm、2dm。
桃汁饮料盒的长、宽、高分别是10cm、7cm、20cm。
啤酒箱的长、宽、高分别是3dm、3dm、3dm。
根据这些信息,你能提出什么问题?
怎样求可乐箱的体积呢?
桃汁饮料盒能盛多少升饮料?
啤酒箱的体积呢?
合作探究
怎样求可乐箱的体积呢
可乐箱的形状是长方体的。
我们借助学具来研究怎样求长方体的体积。
怎样求长方体和正方体的体积呢?
面积的大小就是含有“面积单位”的数量,体积的大小应该是含有“体积单位”的数量吧
2cm
6cm
3cm
可以先把长方体切成1立方厘米的小正方体,再数一数有多少个,就知道体积是多少了。
2cm
6cm
3cm
一共36个小正方体,所以体积是36立方厘米。
也可以用1立方厘米的小正方体木块摆一摆。
长6厘米,一行可以摆6个。
宽2厘米,一层可以摆2行。
2cm
6cm
木块总数:
体积:
高3厘米,可以摆3层。
6×2×3=36(个)
3cm
6cm
2cm
6×2×3=36 (立方厘米)
木块总数:
体积:
4cm
5cm
2cm
5×4×2=40(个)
5×4×2=40 (立方厘米)
摆一个长5厘米,宽4厘米,高2厘米的长方体,并算出它的体积是多少立方厘米。
木块总数:
体积:
3cm
3cm
3cm
3×3×3=27(个)
3×3×3=27(立方厘米)
摆一个棱长是3厘米的正方体,并算出它的体积是多少立方厘米。
回顾刚才的活动过程,想一想,物体的体积与它所含“体积单位”的个数有着怎样的关系?
我发现长方体所含“体积单位”的数量,就是长方体的体积。
我发现长方体所含“体积单位”的数量等于长、宽、高的乘积。
根据以上探索过程,如果V表示长方体的体积,用你能总结出长方体的体积计算公式吗?
V = ɑ · b · h
长方体的体积 = 长×宽×高
b
ɑ
h
长
宽
高
可乐箱的体积是:
7×3×2=42 (立方分米)
答:可乐箱的体积是42dm3。
你会求可乐箱的体积了吗?
怎样求啤酒箱的体积呢
啤酒箱的形状是正方体的。
长方体的长、宽、高相等时,就是正方体了。
长方体的体积=长 × 宽 × 高,正方体的体积······
ɑ
ɑ
ɑ
棱长
棱长
棱长
正方体的体积=棱长×棱长×棱长
V = ɑ · ɑ · ɑ
啤酒箱的体积是:
3×3×3=27 (立方分米)
答:啤酒箱的体积是27dm3。
你会求啤酒箱的体积了吗?
ɑ · ɑ · ɑ 也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:
V = ɑ3
ɑ
ɑ
长方体和正方体底面的面积叫作它们的底面积。
h
b
ɑ
ɑ
底面
底面
ɑ
ɑ
h
b
ɑ
ɑ
底面
底面
你能用同一个公式来表示长方体和正方体体积的计算方法吗?
长方体(或正方体)的体积 = 底面积×高
V = Sh
是不是所有立体图形的体积都等于底面积乘高呢?
试一试
(选题源于《亲子作业本》)
1.填一填。
(1) 一个长方体长10厘米、宽8厘米、高5厘米,这个长方体的体积是( )立方厘米。
(2) 一个正方体的棱长是3分米,这个正方体的体积是( )立方分米。
400
27
(3) 一个长方体的底面积是20平方米,高是5.4米,它的体积是( )立方米。
(4) 正方体的棱长扩大到原来的2倍,它的体积扩大到原来的( )倍。
(选题源于《亲子作业本》)
108
8
(选题源于《亲子作业本》)
2. 计算下面的长方体和正方体的体积。(单位:厘米)
14
6
8
8
8
8
14×8×6=672(立方厘米)
8×8×8=512(立方厘米)
桃汁饮料盒能盛多少升饮料 ( 盒壁厚度不计 )
求桃汁饮料盒能盛多少升饮料,实际上就是求饮料盒的容积是多少。
10×7×20 = 1400 (立方厘米)
1400立方厘米 = 1.4 升
答:桃汁饮料盒能盛 1.4 升饮料。
盒壁厚度不计是什么意思?
长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器里面量长、宽、高。
试一试
(选题源于《亲子作业本》)
1. 选择。
(1) 一个玻璃容器盛满时装有50升水,这个玻璃容器的( )就是50升。
A.体积 B.容积 C.质量
B
(2) 一盒饮料的外包装上写着“净含量:500mL”,那么这盒饮料所占的空间( )500cm3.
A.小于 B.大于 C.等于
(3) 把棱长为5cm的正方体,锯成棱长为1cm的小正方体,可锯成( )个。
A.15 B.25 C.125
(选题源于《亲子作业本》)
B
C
(选题源于《亲子作业本》)
2. 一个长方体鱼缸,从里面量长25cm,宽12cm,高16cm,往里面倒入3L水,水深多少厘米?
3L = 3dm3 = 3000cm3
3000 ÷ 25 ÷ 12 = 10 (cm)
自主练习
第98页*自主练习*第1题
1. 你知道它们的体积各是多少吗
( ) cm3
( ) cm3
42
27
第98页*自主练习*第2题
2. 计算下面图形的体积。
5 × 5 × 8 = 200 (cm3)
第98页*自主练习*第2题
4 × 4 × 4 = 64 (dm3)
20× 4 × 5 = 400 (m3)
第98页*自主练习*第3题
3. 你知道右面这块明代长城砖的体
积是多少立方厘米吗 ( 可用计
算器计算 )
36.8× 18.9 × 9.3 = 6468.336 (cm3)
第98页*自主练习*第4题
4. 右图是一瓶清洁剂。瓶的形状近似长方体,
它长7.3厘米,宽4厘米,高22厘米。这瓶清
洁剂有多少毫升 (瓶壁厚度忽略不计)
37.3× 4 × 22 = 642.4 (cm3)
642.4 cm3= 642.4 mL
第98页*自主练习*第5题
5 .
4 m3 = ( ) dm3
850 dm3 = ( ) m3
2780 mL =( )L
1.4 dm3 = ( )cm3
45 cm3 =( )dm3
2.17 L = ( )mL
4000
1400
0.85
0.045
2.78
2170
第98页*自主练习*第6题
6. 右图中沙雕作品底座的形状是长方体,
它的体积是96立方米,长和宽都是8
米。这个沙雕底座的高是多少米
96÷(8×8) = 1.5(米)
第99页*自主练习*第7题
7 .
一个泄洪坝共有20个泄洪孔,每个泄洪孔的宽是20米,高是125米。泄洪时,通过泄洪孔的水流速度是1.5米/秒。每个泄洪孔每秒能泄洪多少立方米
20×125×1.5 = 3750 (立方米)
第99页*自主练习*第8题
8. 有一块长方体石料,长2.5米,宽 1.6米,高 1.2米。这块石料的体积是多少立方米 用一辆载重量是 15吨的卡车运载这块石料,你觉得可以吗 (每立方米石料重2.7吨)
2.5×1.6×1.2=4.8(立方米)
2.7×4.8=12.96(吨)
12.96<15,可以运载这块石料。
第99页*自主练习*第9题
9. 有一个蓄水池(如下图),长 10米,宽4米,深2 米。
(1) 蓄水池占地面积有多大
10×4 = 40 (平方米)
第99页*自主练习*第9题
(2) 在蓄水池的底面和四周都抹上水泥,抹水泥的面积有多大
10×4 +10×2×2+4×2×2
= 96 (平方米)
第99页*自主练习*第9题
(3) 蓄水池最多能蓄水多少立方米
10×4×2 = 80 (立方米)
第99页*自主练习*第10题
10. 有一段长3米的方木,横截面是一个边长为0.2米的正
方形。50根这样的方木的体积是多少立方米
0.2×0.2×3×50 = 6 (立方米)
第99页*自主练习*第11题
11.哈尔滨冰雪大世界每年用的冰大约能融化成8万立方米的水,它们相当于多少个长20m、宽20m、深2.5m的蓄水池的储水量
80000 ÷ (20×20×2.5) = 80 (个)
8万立方米=80000立方米
第99页*自主练习*第12题
*12 .
生产左图所示的零件需要多少克钢材 ( 每立方厘米钢重7.8克)
7.8 × (15×6×8-5×6×4) = 4680 (克)
测量不规则物体的体积
相关连接
我们学过长方体和正方体的体积计算方法,下面这些物体,你能够求出它们的体积吗?
怎样求这些物体的体积呢?
你能想办法求出它们的体积吗?
西红柿、梨、土豆和石块的形状都是不规则的,不能直接计算出它的体积。
动手做个实验来试一试。
可以用转化的方法,把不规则的物体转化为规则的物体,再求出它们的体积。
测量西红柿体积的实验:
(1) 往水槽里倒水,记下水面的高度。
(2) 再把西红柿放入水槽量杯里(水没过西红柿)。
(3) 记西红柿没入水后水面的高度。
(4) 思考求西红柿体积的方法。
实验活动要求
水面上升了。
将西红柿放入水中
上升的那部分水的体积就是西红柿的体积。
测量西红柿体积的实验:
水面上升了。
将土豆放入水中
上升的那部分水的体积就是土豆的体积。
如果将西红柿换成土豆,你会有什么发现?
西红柿的体积是多少立方厘米呢?
我发现水面上升了。
上升的那部分水的体积就是西红柿的体积。
15×10×12-15×10×10
=1800-1500
=300 (立方厘米)
答:西红柿的体积是300立方厘米。
西红柿的体积是多少立方厘米呢?
西红柿的体积等于现在的体积减去原来的体积。
=300 (立方厘米)
答:西红柿的体积是300立方厘米。
西红柿的体积等于水槽的底面积乘水面上升的高度。
15×10×(12 – 10)
=150×2
西红柿的体积是多少立方厘米呢?
试一试
(选题源于《亲子作业本》)
1. 看图填一填。
(1)番茄的体积是( )m3。 (2)梨的体积是( )cm3。
200
250
(选题源于《亲子作业本》)
2. 小华为了测量一个土豆的体积,做了下面的实验。
(单位:cm)
(1)水的体积是( )。
(2)水和土豆的体积是( )。
(3)土豆的体积是( )。
768cm3
912cm3
144cm3
(选题源于《亲子作业本》)
3. 小方家有一个长40厘米、宽20厘米、高30厘米的长方体玻璃缸,小方买了一些雨花石放了进去,此时水面升高了5厘米。这些雨花石的体积是多少?(玻璃缸的厚度忽略不计)
40×20×5=4000(立方厘米)
自主练习
第101页*自主练习*第1题
1 .
石块的体积是________立方厘米。
150
第101页*自主练习*第1题
一块橡皮的体积是_______立方厘米。
12.5
第101页*自主练习*第2题
2. 妈妈买了体积是11200 立方厘米的假山、水草等饰物,
放进鱼缸完全没入水中,水面升高了多少
11200÷(50×80) =2.8(厘米)
第101页*自主练习*第3题
3. 任意选择一个不规则的物体,想办法测量出它的体积,
把你的活动过程写成一篇数学日记。
根据所选物体和测量过程写数学日记。
你知道吗?
皇冠的秘密
传说,古希腊的一位国王让金匠给他制作了一顶纯金的皇冠。国王怀疑皇冠中掺了白银,于是就让阿基米德检验一下。阿基米德苦思冥想了很长时间,也没找到答案。有一天洗澡时,水溢出了浴缸,他突然受到启发,找到了测量皇冠体积的办法。
他将皇冠和与皇冠同样质量的纯金分别放入水中,发现溢出的水体积不同,从而判断出皇冠不是纯金制成的。
综合练 习
1. 计算下列图形的表面积和体积。
第103页*综合练习*第1题
表面积:
(8×4+6×4+8×6)×2=208(cm2)
体积:
8×4×6=192(cm3)
第103页*综合练习*第1题
表面积:
5×5×6=150(dm2)
体积:
5×5×5=125(dm3)
第103页*综合练习*第1题
表面积:
4×4×2+4×12×4=224 (cm2)
体积:
4×4×12=192(cm3)
2. 填空。
3m2= ( )dm2 0.32m3 =( ) L
5000cm2 =( )dm2
0.05m3 =( )dm3 =( )cm3
3560mL =( ) L = ( )dm3
第103页*综合练习*第2题
300
320
50
50
50000
3.56
3.56
第103页*综合练习*第3题
3. 把调查的数据填在括号里。
肥皂的体积约是( ) 立方厘米。
学校操场的占地面积约是( ) 平方米。
橙汁盒子的容积约是( ) 毫升。
根据实际调查的数据填写。
第103页*综合练习*第4题
4 .
下列图形分别是上面两个长方体的展开图,请你将每个长方体的6个面标在相应的展开图中。
第103页*综合练习*第4题
上面
下面
前面
后面
左面
右面
第103页*综合练习*第4题
上面
下面
前面
后面
左面
右面
第104页*综合练习*第5题
5. 把右图所示的长方体木料切割成最大的正方体,正方体的体积是多少立方分米 最多能切成几个这样的正方体
5×5×5=125(立方分米)
23÷5=4(个)·····3(分米)
最多能切成4个这样的正方体。
第104页*综合练习*第6题
6. 做一个长5分米、宽3分米、高1.5分米
的抽屉(如右图)。至少需要多少平方
分米的木板 (木板的厚度忽略不计)
5×3+5×1.5×2+3×1.5×2=39 (平方分米)
7. 用240厘米长的铁丝做一个最大的正方体框架,然后
用纸板将6个面包起来做一个正方体纸盒,至少需用
多少平方厘米纸板 这个纸盒的体积是多少立方厘米
第104页*综合练习*第7题
240÷12=20(厘米)
20×20×6=2400(平方厘米)
20×20×20=8000(立方厘米)
第104页*综合练习*第8题
8. 填一填。
长方体 长 宽 高 表面积 体积
1 8cm 5cm 4cm
2 18m 12m 7.5m
3 8.1dm 5dm 162dm3
184cm2
160cm3
882m2
1620m3
4dm
185.8dm2
第104页*综合练习*第9题
9. 一个集装箱长9米,宽3.2米,高2.5米。
(1) 制作这样一个集装箱至少需要多
少平方米的钢板
(9×3.2+9×2.5+3.2×2.5)×2=118.6(平方米)
第104页*综合练习*第9题
9. 一个集装箱长9米,宽3.2米,高2.5米。
(2) 这个集装箱的容积大约是多少立
方米 (箱壁厚度忽略不计)
9×3.2×2.5 = 72 (立方米)
第104页*综合练习*第10题
10. 一个长方体,如果高增加3厘米就变成棱长为8厘米的
正方体。原长方体的体积是多少
8×8×(8-3) = 320 (立方厘米)
聪明小屋
右图是由若干个棱长1厘米的小正方体拼成的,它的表面积和体积各是多少
表面积:6×6×2+ 6× 4× 4 = 168 (平方厘米)
体积:6×6×4- 1× 1× 4 = 140 (立方厘米)
我学会了吗?
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
(1) 建造这个游泳池需要挖土多少立方米
50×25×2.2 = 2750 (立方米)
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
(2) 要在它的四壁和底面铺上瓷砖,铺瓷砖部分的面积
是多少平方米
50×25+50×2.2×2+25×2.2×2 = 1580 (平方米)
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
(3) 如果要给这个游泳池注1.8米深的水,已知每小时能
注水150立方米,需用多少小时
50×25×1.8÷150 = 15 (小时)
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
(4) 你还能提出什么问题
(答案不唯一)这个游泳池的底面积是多少平方米?
有趣的溶解现象
将一石块放入水中,石块的体积加上水的体积······
把盐放入水中溶解后就变成了盐水。
盐水的体积=水的体积+盐的体积,对不对
设计个实验验证一下吧。
制订方案
我来设计实验方案。
(1) 取适量的水和盐,想办法分别测量并计算出它们的
体积。
(2) 将盐倒入水中,用玻璃棒搅拌至完全溶解,形成盐
水。测量并计算出盐水的体积。
(3) 比较水和盐的体积之和与盐水的体积是否相等。
实践探究
将盐倒入水中,用玻璃棒搅拌到完全溶解。
我是测量员······
我是记录员······
第_____小组探究记录表
水的体积 盐的体积 盐水的体积
交流展示
全班探究记录汇总表
小组 水的体积 盐的体积 盐水的体积
第一小组
第二小组
第三小组
······
结论
实验报告
实验目的:____________
_____________________
实验方法步骤:________
_____________________
实验结论:____________
_____________________
要让盐完全溶解,测量时要尽量减少误差。
实验报告
实验目的:____________
_____________________
实验方法步骤:________
_____________________
实验结论:____________
_____________________
通过实验,我们发现······
实验报告
实验目的:____________
_____________________
实验方法步骤:________
_____________________
实验结论:____________
_____________________
根据实验和查阅的资料,我写出了实验报告······
总结反思
只凭一次实验不能马上得出结论,汇总各个小组的实验结果才能得出结论。
为什么会产生这样的现象呢 把糖放入水中,会不会也有类似的现象呢
我们查一查资料,看有没有溶解后总体积增加的现象。
这次数学实践活动我用到的数学知识有······
课后作业
七 包装盒
——长方体和正方体
长方体和正方体的认识
情境导入
从图中,你能知道哪些数学信息?
这些图形都是立体图形。
这些图形都是立体图形。
根据这些信息,你能提出什么问题?
长方体有哪些特征?
正方体有哪些特征?
合作探究
长方体有哪些特征
我们借助学具来研究。
长方体
面
面
面
两个面相交的线叫作棱,
( léng )
棱
三条棱相交的点叫作顶点。
我发现长方体有6个面,它们是长方形(有时有两个相对的面是正方形),相对的面……
长方体有8个顶点。
长方体有12条棱,按长度可以分成3组,相对的4条棱……
长方体有6个面,都是长方形(可能有两个相对的面是正方形)。
面的特点:
上下两个面相同
面的特点:
左右两个面相同
面的特点:
结论:长方体相对的面完全相同。
前后两个面相同
面的特点:
长方体共有12条棱。
棱的特点:
长方体有12条棱,可以分成3组,相对的4条棱的长度相等。
棱的特点:
长方体共有8个顶点。
顶点的特点:
从一个方向观察一个长方体,最多能同时看到几个面?
从一个方向观察一个长方体,最多能同时看到3个面。
长
宽
高
相交于一个顶点的三条棱的长度,分别叫作长方体的长、宽、高。
试一试
(选题源于《亲子作业本》)
看图回答问题。
(1) 这个纸巾盒的前面是什么形状?长和宽各是多少?和它相同的面是哪个?
前面是长方形。
长:24cm、宽9cm。
后面
(选题源于《亲子作业本》)
(2) 它的右面是什么形状?长和宽各是多少?和它相同的面是哪个?
右面是长方形。
长:12cm、宽9cm。
左面
(选题源于《亲子作业本》)
(3) 哪几个面的长是24cm,宽是12cm
上面和下面
正方体有哪些特征
我们借助学具来研究一下吧 !
正方体有 6个面它们是完全相同的正方形。
正方体有8个顶点12 条棱,每条棱的长度都相等。
上下两个面相同
面的特点:
左右两个面相同
面的特点:
6个面是完全相同的正方形
前后两个面相同
面的特点:
正方体有12条棱,所有的棱长度相等。
棱的特点:
顶点的特点:
正方体共有8个顶点。
正方体与长方体有什么联系与区别
正方形是特殊的长方形,正方体是不是特殊的长方体呢
我们整理一下吧。
面 棱 顶点
长方体
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
相对的4条棱长度相等(可能有8条棱长度相等)
8个
面 棱 顶点
正方体
6个面都是
正方形,6
个面完全相同。
12条棱长
度相等
8个
正方体是特殊的长方体。可以用右图表示正方体和长方体的关系。
长方体
正方体
试一试
(选题源于《亲子作业本》)
1. 填空。
(1) 相交于一个顶点的三条棱的长度,分别叫作长方体的( )、( )、( )。
长
宽
高
(选题源于《亲子作业本》)
(2) 看图,写一写长方体的长、宽、高各是多少。
5 cm
2 cm
5 cm
长( )cm
宽( )cm
高( )cm
5
2
5
(选题源于《亲子作业本》)
12 cm
7 cm
4 cm
长( )cm
宽( )cm
高( )cm
12
7
4
(3) 请把正方体和长方体的名称填入下图中。
(选题源于《亲子作业本》)
( )
( )
长方体
正方体
(选题源于《亲子作业本》)
(4)长方体有( )个面,( )条棱,( )个顶点,相对的两个面( ),相对的棱的长度( )。
(5) 正方体有( )个面,( )条棱,( )个顶点,所有的面都( ),所有棱的长度都( )。
(6)长方体的面都是( )形,特殊的长方体有两个相对的面是( )形,此时其余四个面的面积( )。
6
12
8
完全相同
相等
6
12
8
相同
相等
长方
正方
相等
自主练习
第84页*自主练习*第1题
1. 说一说。
(1) .墨汁盒的上面是什么形状 与它
相对的是哪个面
墨汁盒的上面是长方形;与它相对的面是下面。
第84页*自主练习*第1题
(2) 前面的长和宽各是多少 哪个面
与它相同
前面的长是12厘米,宽是5厘米;后面与它相同。
第84页*自主练习*第1题
(3) 哪个面的长是12厘米,宽是3厘米
左、右两个面的长是12厘米,宽是3厘米。
第84页*自主练习*第2题
2. 说出每个长方体的长、宽、高各是多少。
长:7cm
宽:5cm
高:6cm
第84页*自主练习*第2题
长:3 dm
宽:2 dm
高:4 dm
第84页*自主练习*第2题
长:2 m
宽:0.5 m
高:0.5 m
第84页*自主练习*第3题
3. 观察右图,回答问题。
(1) 两个储物箱的形状都是正方体吗
不都是,第一个储物箱的形状是正方体,第二个储物箱的形状是长方体。
第84页*自主练习*第3题
(2) 正方体储物箱的棱长是多少 哪几个面完全相同
棱长是6分米,6个面完全相同。
第84页*自主练习*第3题
(3) 长方体储物箱的长、宽、高各是多少 哪几个面完全相同
长是7分米,宽是6分米,高是6分米。上、下、左、右4个面完全相同,前、后2个面完全相同。
第84页*自主练习*第4题
4. 量一量。
以其中一种物品为例,说一说每个面的长和宽各是多少。
提示:根据测量所得的数据填表并回答问题。
第85页*自主练习*第5题
5. 哪几个面可以围成一个长方体
①号、②号、③号、⑤号、⑥号和⑦号6个面可以围成一个长方体。
第85页*自主练习*第6题
6. 计算下图中长方体和正方体每个面的面积。
前、后面:13×5=65 (平方厘米)
上、下面:13×2=26 (平方厘米)
左、右面:5×2=10 (平平方厘米)
第85页*自主练习*第6题
每个面的面积:
8×8=64 (平方米)
第85页*自主练习*第6题
前、后面:18×5=90(平方分米)
上、下面:5×2=10(平方分米)
左、右面:18×2=36(平方分米)
第85页*自主练习*第7题
7. 用12个棱长是1厘米的小正方体拼成一个长方体,有几种不同的拼法 拼成的长方体的长、宽、高各是多少
有4种不同的拼法,每种拼法的长、宽、高分别是12厘米、1厘米、1厘米;6厘米、2厘米、1厘米;4厘米、3厘米、1厘米;3厘米、2厘米、2厘米。
(摆放方式不同,对应的长、宽、高就不同)
第85页*自主练习*第8题
一个长方体广告灯箱长5米,宽0.5米,高3米。灯箱的框架用铝条镶嵌,至少需要多少米铝条
8 .
(5+0.5+3) ×4=34 (米)
方形西瓜
你见过方形西瓜吗 你知道它们是怎样长成的吗
瓜农们将幼瓜置于按一定规格做好的长方体形状的透明玻璃模具里,幼瓜最终就长成了方形西瓜。
这种瓜不仅为运输储藏带来
方便,还会因外形奇特而更加
吸引消费者。
你知道了吗?
长方体和正方体的表面积
情景导入
从图中,你能知道哪些数学信息?
根据这些信息,你能提出什么问题?
制作这样一个电脑包装箱至少需要多少平方厘米纸板?
做一个化妆品盒子至少需要多少平方厘米纸板?
合作探究
制作这样一个电脑包装箱至少需要多少平方厘米纸板
要求需要多少平方厘米纸板就是求电脑包装箱6个面的总面积。
怎样求长方体6个面的总面积呢?
我们借助长方体表面的展开图来研究吧。
将一个长方体的表面展开:
上
上
下
前
后
上
下
前
后
左
上
下
前
后
左
右
上
下
前
后
左
右
下
前
后
上
左
右
上
下
前
后
左
右
上
前
右
你能在展开图上找到其他的3个面吗 哪些面的面积相等
分别求出相对面的面积,再相加。
前、后面:50×30×2=
左、右面:20×30×2=
上、下面:50×20×2=
总面积:_______________________________________
3000 (平方厘米)
1200 (平方厘米)
2000 (平方厘米)
3000 +1200 +2000 =6200 (平方厘米)
先求前面、右面、上面3个面的面积之和,再乘2。
(50×30+20×30+50×20)×2
=__________________________
=__________________________
答:制作这样一个电脑包装箱至少需要_________平方厘米纸板。
(1500 + 600 + 1000)×2
3100×2
= 6200 (平方厘米)
6200
根据刚才的解题过程,你能总结出长方体的表面积计算公式吗?
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2
长方体的表面积 = (长×宽+长×高+宽×高)×2
长方体的表面积计算公式。
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2
长方体的表面积 = (长×宽+长×高+宽×高)×2
试一试
(选题源于《亲子作业本》)
计算下面图形的表面积。
2 m
0.5 m
0.5 m
(1)
2×0.5×4+0.5×0.5×2
= 4+0.5
= 4.5(m2)
(选题源于《亲子作业本》)
8 m
7 m
5 m
(2)
(5×8+5×7+7×8)×2
=131×2
=262(m2)
做一个化妆品盒子至少需要多少平方厘米纸板
求做一个化妆品盒子至少需要多少平方厘米纸板,实际就是求······
求正方体6个面的总面积。
怎样求正方体6个面的总面积呢?
正方体的6个面是完全相同的正方形,只要先求出一个面的面积,再乘6即可。
5×5×6
=_____________
=_____________
25×6
150(平方里面)
答:做一个化妆品盒子至少需要_____平方厘米纸板。
150
你能总结出正方体的表面积计算公式吗?
正方体的表面积=棱长×棱长×6
长方体或正方体6个面的总面积,叫作它的表面积。
试一试
(选题源于《亲子作业本》)
1. 计算下面图形的表面积。
4 m
4 m
4 m
4×4×6
= 16×6
= 96 (m2)
(选题源于《亲子作业本》)
2. 一个塑料板制成的文具盒,长是2.2分米,宽是8厘米,高是2厘米,它需要多少平方厘米的塑料板?制作6个这样的文具盒需要塑料板多少平方厘米?
2.2分米=22厘米
(22×8+22×2+8×2)×2=472(平方厘米)
472×6=2832(平方厘米)
(选题源于《亲子作业本》)
3. 下面是一个长方体的展开图,求该长方体的表面积。
(单位:厘米)
(8×6+8×2+6×2)×2=152 (平方厘米)
自主练习
第88页*自主练习*第1题
1.下面的平面图哪些可以折成长方体或正方体
图①、图③可以折成长方体,图④可以折成正方体。
第88页*自主练习*第2题
2. 右图是一个长方体。
(1) 上面的面积是_______平方厘米。
(2) 前面的面积是_______平方厘米。
(3) 右面的面积是_______平方厘米。
(4) 表面积是________平方厘米。
24
30
20
148
第88页*自主练习*第3题
3. 右图是一个长方体。
(3×2 +3×1+2×1)×2 = 22(dm2)
第88页*自主练习*第3题
5×5×6=150(cm2)
第88页*自主练习*第3题
(0.4×0.4 +0.4×0.7+0.4×0.7)×2 = 1.44 (m2)
第88页*自主练习*第4题
4. 包装形如右图的正方体礼盒,至少需要多少平方分米的包装纸
12×12×6=864 (平方厘米)
864平方厘米=8.64平方分米
第88页*自主练习*第5题
做这样一个手提袋至少需要多少平方厘米的纸板
5 . (1)
30×40×2+30×10+10+40×2=3500 (平方厘米)
第89页*自主练习*第5题
鱼缸的4个侧面是用玻璃做的。做这样一个鱼缸至少需要多少平方厘米的玻璃
(2)
(60×80+160×80)×2=35200 (平方厘米)
第89页*自主练习*第6题
6. 方形雨水管横截面的长是10厘米,宽是8厘米。每一节雨水管长2米。做25节这样的雨水管至少需要多少平方米铁皮
10厘米=0.1米
8厘米=0.08米
(0.1×2 + 0.08×2)×2×25 = 18 (平方米)
第89页*自主练习*第7题
7.一间教室长9米,宽7米,高3米。要粉刷教室的屋顶和四面墙壁 ( 除去门窗和黑板的面积29.6平方米),粉刷面积是多少平方米 如果平均每平方米用0.2千克涂料,至少需要多少千克涂料
9×7+9×3×2+7×3×2-29.6 =129.4(平方米)
0.2×129.4 = 25.88 (千克)
第89页*自主练习*第8题
8. (1) 量一量《新华字典》的长、宽、高分别是多少,然后算出它的表面积。
提示:先用尺子测量出《新华字典》的长、宽、高,再算出它的表面积,最后用纸把2本《新华字典》包起来,看一看有几种包法,哪种包法最省纸。
(2) 如果用纸把2本《新华字典》包起来,有几种包法 哪种包法最省纸
聪明小屋
(1) 2个棱长1厘米的正方体,它们的表面积总和是多
少平方厘米 把它们拼成一个长方体后,表面积减
少了多少平方厘米
1×1×6×2=12 (平方厘米)
1×1×2=2 (平方厘米)
聪明小屋
(2) 3个这样的正方体拼成一个长方体后,表面积减少
了多少平方厘米 4个呢
1×1×4=4 (平方厘米)
1×1×6=6 (平方厘米)
聪明小屋
(3) 你有什么发现
发现:每增加一个正方体,拼成的长方体的表面积就比正方体的表面积总和少2个正方形的面积,即按这样的拼法,n个棱长1厘米的正方体拼成一个长方体后,减少的表面积为[1×1×2×(n-1)]平方厘米。
聪明小屋
(4) 按这样的拼法,20个小正方体拼成一个长方体后,
表面积减少了多少平方厘米
1×1×2× (20-1) =38 (平方厘米)
体积、溶积及单位间的进率
情景导入
从图中,你知道了哪些数学信息?
体积:50×50×20
体积:40×30×20
体积:50×50×20
体积:40×30×20
根据这些信息,你能提出什么问题?
什么是体积?
合作探究
什么是体积?
我们做个实验吧。
实验一要求
2. 用手提绳子将石头浸入玻璃杯的水中,观察放入石
头后水位有的变化情况。
3. 说说观察的结果,想一想,这说明了什么?
1. 准备盛有半杯红色水的玻璃杯和用绳子捆着的石
头一块。
1. 准备2个同样的杯子。第一个杯子装满沙子,第二
个杯子空杯。
2. 将一块木块放入第二个杯子中,然后从第一个杯
子向第二个杯子中倒沙子,倒满为止。
3. 说说观察的结果,想一想,这说明了什么?
实验二要求
将石块放入水中
石块占了水槽的空间
实验一:
水面上升
我发现水槽里的水面升高了。因为······
实验二:
将木块放入空杯中
木块占了空杯的空间
我发现······
物体所占空间的大小叫作物体的体积。
空气 、橙汁、冰箱都占空间。
你能说说生活中哪些物体占空间吗?
下面的长方体和正方体,谁的体积大?
大小不明显,看不出来,需要计量。
用什么计量比较合适呢?
我知道用 能计量出长方形、正方形的面积。
15个
16个
我猜想可以用 计量体积。
24个
27个
体积单位可以写成:
面积单位有平方厘米、平方分米······体积单位有哪些呢
常用的面积单位有:平方厘米 平方分米 平方米
常用的体积单位有:
立方厘米
立方分米
cm3
dm3
m3
立方米
试一试
(选题源于《亲子作业本》)
1. 填空。
(1) 物体所占( )的大小叫作物体的体积。
(2) 把冰箱、文具盒和微波炉进行比较,( ) 的体积最大,( ) 的体积最小。
(3) 棱长是1cm、1dm和1m的正方体的体积分别是1( )、1( )和1( )。
空间
冰箱
文具盒
cm3
dm3
m3
(选题源于《亲子作业本》)
2. 选择。
(1) 体积单位和面积单位相比较,( )。
A.体积单位大 B.面积单位大 C.无法比较
(2) 有两个棱长都是1分米的正方体,一个是木块,另一个是铁块。它们的体积相比,( )大。
A.铁块 B.木块 C.同样
C
C
棱长为1厘米的正方体,体积是1立方厘米。
1cm
1cm
1cm
1立方厘米有多大呢?
一个手指尖的体积大约是1立方厘米。
一粒花生米的体积大约是1立方厘米。
生活中哪些物体的体积大约是1立方厘米?
牛奶箱的体积用立方厘米作单位来测量合适吗?
1立方厘米太小,用1立方分米作单位比较合适。
1cm
1cm
1cm
1dm
1dm
1dm
棱长为1分米的正方体,体积是1立方分米。
1立方分米有多大呢?
棱长为1分米的正方体,体积是1立方分米。
粉笔盒的体积大约是1立方分米。
集装箱的体积用立方分米作单位来测量合适吗?
1立方分米太小,用1立方米作单位比较合适。
1dm
1dm
1dm
1m
1m
1m
棱长为1米的正方体,体积是1立方米。
1立方米有多大呢?
说一说,生活中哪些物体的体积大约是1立方米?
棱长为1米的正方体,体积是1立方米。
装29英寸电视机的纸箱的体积大约是1立方米。
想一想,在体积单位的探索过程中,我们运用了什么方法?
类比
平方厘米
平方分米
平方米
常用的面积单位
类 比
立方厘米
立方分米
立方米
常用的面积单位
1. 判断。
(1) 把一块正方体铁块铸成一块长方体,体积不变。
( )
(2) 棱长是1米的正方体,它的体积一定是1立方米。
( )
(3) 一个烟盒的体积大约是96立方分米。( )
试一试
(选题源于《亲子作业本》)
2.下面的图形都是用棱长为1cm的小正方体摆成的,写出
它们的体积。
( ) cm3
( ) cm3
( ) cm3
(选题源于《亲子作业本》)
9
6
13
( ) cm3
( ) cm3
( ) cm3
(选题源于《亲子作业本》)
7
6
10
(选题源于《亲子作业本》)
3. 在括号里填上合适的单位。
文具盒的体积约是200( )。 西瓜的体积约是15( )。
手机的体积约是70( )。 冰箱的体积约是1.2( )。
cm3
dm3
cm3
m3
牙膏盒的体积约是120( )。
生日蛋糕的体积约是16( )。
(选题源于《亲子作业本》)
cm3
dm3
想一想,用棱长1厘米的小正方体摆成下面的长方体和正方体,它们的体积各是多少
计量一个物体的体积,要看这个物体含有多少个“体积单位”。
1立方分米是多少立方厘米呢
我用1立方厘米的方木块摆。
一行摆10个,一层摆10行,摆10层,我发现······
1立方分米=1000立方厘米
1立方米=1000立方分米
在括号里填上合适的数。
2.25 m3= ( ) dm3 760 cm3= ( ) dm3
76000 cm3= ( ) dm3= ( ) m3
0.8 dm3= ( ) cm3
7.56 m3= ( ) dm3= ( ) cm3
(选题源于《亲子作业本》)
试一试
2250
0.76
76
0.076
800
7560
7560000
哪个奶盒装的牛奶多一些
哪个盒内的空间大,哪个就装得多。
哪个盒内的空间大,哪个就装得多。
用同样的杯子量一量······
红色牛奶盒装的牛奶多。
容器所能容纳物体的体积,叫作它们的容积。
计量容积一般用体积单位。但是计量液体的体积,如水、油等,常用容积单位升与毫升。升与毫升可以分别写成L和mL。
10mL
500mL
1L
你知道计量容积的单位有哪些吗?
1升 =1立方分米
1升 = 1000毫升
1毫升 =1立方厘米
(选题源于《亲子作业本》)
试一试
1. 填空。
(1) 物体所占( )叫作物体的体积,容器( )叫作容器的容积。
(2) 课桌的体积比书本的体积( )。
空间的大小
所能容纳物体的体积
大
(3) 在括号里填上合适的单位名称。
① 一个油桶能装油5( )。
② 一盒纯牛奶大约是250( )。
③集装箱的容积大约是40( )。
④ 一个长方体游泳池的容积大约是800( )。
(选题源于《亲子作业本》)
L
mL
m3
m3
(选题源于《亲子作业本》)
2. 判断。
(1) 两个物体相比较,容积大的物体体积也比较大。
( )
(2) 物体一定有体积,但不一定有容积。( )
(3) 一个木盒和一个纸盒的体积相等,它们的容积也相等。( )
(选题源于《亲子作业本》)
3. 选择。
(1) 一个玻璃瓶可装350毫升的饮料,这个瓶子的( )是350毫升。瓶子占地32平方厘米,是指瓶子的( )。
A.底面积 B.体积 C.容积
(2) 物体的体积和容积的根本区别是( )不同。
A.计量单位 B.意义 C.计算方法
C
A
B
(3) 一瓶牛奶,牛奶的体积就是瓶子的( )。
A.容积 B.体积 C.质量
(选题源于《亲子作业本》)
A
(选题源于《亲子作业本》)
4. 单位换算。
5m3= ( )dm3 530cm3 =( )dm3
2.3m3 =( )dm3 =( )L
9L 62mL =( )L
7.8L = ( )dm3 =( )mL
2.6dm3 =( )L =( )cm3
5000
0.53
2300
2300
9.062
7.8
7.8
2.6
2600
自主练习
1. 说一说谁的体积大。
第93页*自主练习*第1题
第93页*自主练习*第2题
2. 下面的图形都是用棱长1厘米的小正方体摆成的,说
一说它们的体积各是多少立方厘米。
8立方厘米
7立方厘米
7立方厘米
第94页*自主练习*第3题
3. 填上合适的单位名称。
墨水瓶的容积约是60( )。
微波炉的体积约是40( )。
毫升
立方分米
第94页*自主练习*第3题
酸奶盒的容积约是240( )。
矿泉水桶的容积约是20( )。
毫升
升
第94页*自主练习*第3题
集装箱的体积约是50( )。
文具盒的体积约是200( )。
立方米
立方厘米
第94页*自主练习*第4题
4 .
3.03dm3= ( )L
800cm3= ( )dm3
320mL= ( )L
0.5m3= ( )dm3
4526mL= ( )cm3
2340L= ( ) m3
3.03
500
0.8
4526
0.32
2.34
第94页*自主练习*第5题
5. 整理并填表。
常用单位名称 相邻两个单位间的进率
长度单位
面积单位
体积单位
米、分米、厘米
10
平方米、平方分米、平方厘米
100
立方米、立方分米、立方厘米
1000
第94页*自主练习*第6题
6. 估一估,填一填。
5升
( )升
2000毫升
( ) 毫升
2.5
700
第94页*自主练习*第7题
7.一瓶矿泉水有500mL,纸杯的容积约是120mL。
(1) 一瓶矿泉水大约能倒满几杯
(2) 一个人平均每天大约需要喝1300毫升的水,如果
使用这样的纸杯,每天大约需要喝多少杯水
(1) 大约能倒满4杯。
(2) 每天大约需要喝11杯水。
长方体和正方体体积
情景导入
从图中,你知道了哪些数学信息?
可乐箱的长、宽、高分别是7dm、3dm、2dm。
桃汁饮料盒的长、宽、高分别是10cm、7cm、20cm。
啤酒箱的长、宽、高分别是3dm、3dm、3dm。
可乐箱的长、宽、高分别是7dm、3dm、2dm。
桃汁饮料盒的长、宽、高分别是10cm、7cm、20cm。
啤酒箱的长、宽、高分别是3dm、3dm、3dm。
根据这些信息,你能提出什么问题?
怎样求可乐箱的体积呢?
桃汁饮料盒能盛多少升饮料?
啤酒箱的体积呢?
合作探究
怎样求可乐箱的体积呢
可乐箱的形状是长方体的。
我们借助学具来研究怎样求长方体的体积。
怎样求长方体和正方体的体积呢?
面积的大小就是含有“面积单位”的数量,体积的大小应该是含有“体积单位”的数量吧
2cm
6cm
3cm
可以先把长方体切成1立方厘米的小正方体,再数一数有多少个,就知道体积是多少了。
2cm
6cm
3cm
一共36个小正方体,所以体积是36立方厘米。
也可以用1立方厘米的小正方体木块摆一摆。
长6厘米,一行可以摆6个。
宽2厘米,一层可以摆2行。
2cm
6cm
木块总数:
体积:
高3厘米,可以摆3层。
6×2×3=36(个)
3cm
6cm
2cm
6×2×3=36 (立方厘米)
木块总数:
体积:
4cm
5cm
2cm
5×4×2=40(个)
5×4×2=40 (立方厘米)
摆一个长5厘米,宽4厘米,高2厘米的长方体,并算出它的体积是多少立方厘米。
木块总数:
体积:
3cm
3cm
3cm
3×3×3=27(个)
3×3×3=27(立方厘米)
摆一个棱长是3厘米的正方体,并算出它的体积是多少立方厘米。
回顾刚才的活动过程,想一想,物体的体积与它所含“体积单位”的个数有着怎样的关系?
我发现长方体所含“体积单位”的数量,就是长方体的体积。
我发现长方体所含“体积单位”的数量等于长、宽、高的乘积。
根据以上探索过程,如果V表示长方体的体积,用你能总结出长方体的体积计算公式吗?
V = ɑ · b · h
长方体的体积 = 长×宽×高
b
ɑ
h
长
宽
高
可乐箱的体积是:
7×3×2=42 (立方分米)
答:可乐箱的体积是42dm3。
你会求可乐箱的体积了吗?
怎样求啤酒箱的体积呢
啤酒箱的形状是正方体的。
长方体的长、宽、高相等时,就是正方体了。
长方体的体积=长 × 宽 × 高,正方体的体积······
ɑ
ɑ
ɑ
棱长
棱长
棱长
正方体的体积=棱长×棱长×棱长
V = ɑ · ɑ · ɑ
啤酒箱的体积是:
3×3×3=27 (立方分米)
答:啤酒箱的体积是27dm3。
你会求啤酒箱的体积了吗?
ɑ · ɑ · ɑ 也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:
V = ɑ3
ɑ
ɑ
长方体和正方体底面的面积叫作它们的底面积。
h
b
ɑ
ɑ
底面
底面
ɑ
ɑ
h
b
ɑ
ɑ
底面
底面
你能用同一个公式来表示长方体和正方体体积的计算方法吗?
长方体(或正方体)的体积 = 底面积×高
V = Sh
是不是所有立体图形的体积都等于底面积乘高呢?
试一试
(选题源于《亲子作业本》)
1.填一填。
(1) 一个长方体长10厘米、宽8厘米、高5厘米,这个长方体的体积是( )立方厘米。
(2) 一个正方体的棱长是3分米,这个正方体的体积是( )立方分米。
400
27
(3) 一个长方体的底面积是20平方米,高是5.4米,它的体积是( )立方米。
(4) 正方体的棱长扩大到原来的2倍,它的体积扩大到原来的( )倍。
(选题源于《亲子作业本》)
108
8
(选题源于《亲子作业本》)
2. 计算下面的长方体和正方体的体积。(单位:厘米)
14
6
8
8
8
8
14×8×6=672(立方厘米)
8×8×8=512(立方厘米)
桃汁饮料盒能盛多少升饮料 ( 盒壁厚度不计 )
求桃汁饮料盒能盛多少升饮料,实际上就是求饮料盒的容积是多少。
10×7×20 = 1400 (立方厘米)
1400立方厘米 = 1.4 升
答:桃汁饮料盒能盛 1.4 升饮料。
盒壁厚度不计是什么意思?
长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器里面量长、宽、高。
试一试
(选题源于《亲子作业本》)
1. 选择。
(1) 一个玻璃容器盛满时装有50升水,这个玻璃容器的( )就是50升。
A.体积 B.容积 C.质量
B
(2) 一盒饮料的外包装上写着“净含量:500mL”,那么这盒饮料所占的空间( )500cm3.
A.小于 B.大于 C.等于
(3) 把棱长为5cm的正方体,锯成棱长为1cm的小正方体,可锯成( )个。
A.15 B.25 C.125
(选题源于《亲子作业本》)
B
C
(选题源于《亲子作业本》)
2. 一个长方体鱼缸,从里面量长25cm,宽12cm,高16cm,往里面倒入3L水,水深多少厘米?
3L = 3dm3 = 3000cm3
3000 ÷ 25 ÷ 12 = 10 (cm)
自主练习
第98页*自主练习*第1题
1. 你知道它们的体积各是多少吗
( ) cm3
( ) cm3
42
27
第98页*自主练习*第2题
2. 计算下面图形的体积。
5 × 5 × 8 = 200 (cm3)
第98页*自主练习*第2题
4 × 4 × 4 = 64 (dm3)
20× 4 × 5 = 400 (m3)
第98页*自主练习*第3题
3. 你知道右面这块明代长城砖的体
积是多少立方厘米吗 ( 可用计
算器计算 )
36.8× 18.9 × 9.3 = 6468.336 (cm3)
第98页*自主练习*第4题
4. 右图是一瓶清洁剂。瓶的形状近似长方体,
它长7.3厘米,宽4厘米,高22厘米。这瓶清
洁剂有多少毫升 (瓶壁厚度忽略不计)
37.3× 4 × 22 = 642.4 (cm3)
642.4 cm3= 642.4 mL
第98页*自主练习*第5题
5 .
4 m3 = ( ) dm3
850 dm3 = ( ) m3
2780 mL =( )L
1.4 dm3 = ( )cm3
45 cm3 =( )dm3
2.17 L = ( )mL
4000
1400
0.85
0.045
2.78
2170
第98页*自主练习*第6题
6. 右图中沙雕作品底座的形状是长方体,
它的体积是96立方米,长和宽都是8
米。这个沙雕底座的高是多少米
96÷(8×8) = 1.5(米)
第99页*自主练习*第7题
7 .
一个泄洪坝共有20个泄洪孔,每个泄洪孔的宽是20米,高是125米。泄洪时,通过泄洪孔的水流速度是1.5米/秒。每个泄洪孔每秒能泄洪多少立方米
20×125×1.5 = 3750 (立方米)
第99页*自主练习*第8题
8. 有一块长方体石料,长2.5米,宽 1.6米,高 1.2米。这块石料的体积是多少立方米 用一辆载重量是 15吨的卡车运载这块石料,你觉得可以吗 (每立方米石料重2.7吨)
2.5×1.6×1.2=4.8(立方米)
2.7×4.8=12.96(吨)
12.96<15,可以运载这块石料。
第99页*自主练习*第9题
9. 有一个蓄水池(如下图),长 10米,宽4米,深2 米。
(1) 蓄水池占地面积有多大
10×4 = 40 (平方米)
第99页*自主练习*第9题
(2) 在蓄水池的底面和四周都抹上水泥,抹水泥的面积有多大
10×4 +10×2×2+4×2×2
= 96 (平方米)
第99页*自主练习*第9题
(3) 蓄水池最多能蓄水多少立方米
10×4×2 = 80 (立方米)
第99页*自主练习*第10题
10. 有一段长3米的方木,横截面是一个边长为0.2米的正
方形。50根这样的方木的体积是多少立方米
0.2×0.2×3×50 = 6 (立方米)
第99页*自主练习*第11题
11.哈尔滨冰雪大世界每年用的冰大约能融化成8万立方米的水,它们相当于多少个长20m、宽20m、深2.5m的蓄水池的储水量
80000 ÷ (20×20×2.5) = 80 (个)
8万立方米=80000立方米
第99页*自主练习*第12题
*12 .
生产左图所示的零件需要多少克钢材 ( 每立方厘米钢重7.8克)
7.8 × (15×6×8-5×6×4) = 4680 (克)
测量不规则物体的体积
相关连接
我们学过长方体和正方体的体积计算方法,下面这些物体,你能够求出它们的体积吗?
怎样求这些物体的体积呢?
你能想办法求出它们的体积吗?
西红柿、梨、土豆和石块的形状都是不规则的,不能直接计算出它的体积。
动手做个实验来试一试。
可以用转化的方法,把不规则的物体转化为规则的物体,再求出它们的体积。
测量西红柿体积的实验:
(1) 往水槽里倒水,记下水面的高度。
(2) 再把西红柿放入水槽量杯里(水没过西红柿)。
(3) 记西红柿没入水后水面的高度。
(4) 思考求西红柿体积的方法。
实验活动要求
水面上升了。
将西红柿放入水中
上升的那部分水的体积就是西红柿的体积。
测量西红柿体积的实验:
水面上升了。
将土豆放入水中
上升的那部分水的体积就是土豆的体积。
如果将西红柿换成土豆,你会有什么发现?
西红柿的体积是多少立方厘米呢?
我发现水面上升了。
上升的那部分水的体积就是西红柿的体积。
15×10×12-15×10×10
=1800-1500
=300 (立方厘米)
答:西红柿的体积是300立方厘米。
西红柿的体积是多少立方厘米呢?
西红柿的体积等于现在的体积减去原来的体积。
=300 (立方厘米)
答:西红柿的体积是300立方厘米。
西红柿的体积等于水槽的底面积乘水面上升的高度。
15×10×(12 – 10)
=150×2
西红柿的体积是多少立方厘米呢?
试一试
(选题源于《亲子作业本》)
1. 看图填一填。
(1)番茄的体积是( )m3。 (2)梨的体积是( )cm3。
200
250
(选题源于《亲子作业本》)
2. 小华为了测量一个土豆的体积,做了下面的实验。
(单位:cm)
(1)水的体积是( )。
(2)水和土豆的体积是( )。
(3)土豆的体积是( )。
768cm3
912cm3
144cm3
(选题源于《亲子作业本》)
3. 小方家有一个长40厘米、宽20厘米、高30厘米的长方体玻璃缸,小方买了一些雨花石放了进去,此时水面升高了5厘米。这些雨花石的体积是多少?(玻璃缸的厚度忽略不计)
40×20×5=4000(立方厘米)
自主练习
第101页*自主练习*第1题
1 .
石块的体积是________立方厘米。
150
第101页*自主练习*第1题
一块橡皮的体积是_______立方厘米。
12.5
第101页*自主练习*第2题
2. 妈妈买了体积是11200 立方厘米的假山、水草等饰物,
放进鱼缸完全没入水中,水面升高了多少
11200÷(50×80) =2.8(厘米)
第101页*自主练习*第3题
3. 任意选择一个不规则的物体,想办法测量出它的体积,
把你的活动过程写成一篇数学日记。
根据所选物体和测量过程写数学日记。
你知道吗?
皇冠的秘密
传说,古希腊的一位国王让金匠给他制作了一顶纯金的皇冠。国王怀疑皇冠中掺了白银,于是就让阿基米德检验一下。阿基米德苦思冥想了很长时间,也没找到答案。有一天洗澡时,水溢出了浴缸,他突然受到启发,找到了测量皇冠体积的办法。
他将皇冠和与皇冠同样质量的纯金分别放入水中,发现溢出的水体积不同,从而判断出皇冠不是纯金制成的。
综合练 习
1. 计算下列图形的表面积和体积。
第103页*综合练习*第1题
表面积:
(8×4+6×4+8×6)×2=208(cm2)
体积:
8×4×6=192(cm3)
第103页*综合练习*第1题
表面积:
5×5×6=150(dm2)
体积:
5×5×5=125(dm3)
第103页*综合练习*第1题
表面积:
4×4×2+4×12×4=224 (cm2)
体积:
4×4×12=192(cm3)
2. 填空。
3m2= ( )dm2 0.32m3 =( ) L
5000cm2 =( )dm2
0.05m3 =( )dm3 =( )cm3
3560mL =( ) L = ( )dm3
第103页*综合练习*第2题
300
320
50
50
50000
3.56
3.56
第103页*综合练习*第3题
3. 把调查的数据填在括号里。
肥皂的体积约是( ) 立方厘米。
学校操场的占地面积约是( ) 平方米。
橙汁盒子的容积约是( ) 毫升。
根据实际调查的数据填写。
第103页*综合练习*第4题
4 .
下列图形分别是上面两个长方体的展开图,请你将每个长方体的6个面标在相应的展开图中。
第103页*综合练习*第4题
上面
下面
前面
后面
左面
右面
第103页*综合练习*第4题
上面
下面
前面
后面
左面
右面
第104页*综合练习*第5题
5. 把右图所示的长方体木料切割成最大的正方体,正方体的体积是多少立方分米 最多能切成几个这样的正方体
5×5×5=125(立方分米)
23÷5=4(个)·····3(分米)
最多能切成4个这样的正方体。
第104页*综合练习*第6题
6. 做一个长5分米、宽3分米、高1.5分米
的抽屉(如右图)。至少需要多少平方
分米的木板 (木板的厚度忽略不计)
5×3+5×1.5×2+3×1.5×2=39 (平方分米)
7. 用240厘米长的铁丝做一个最大的正方体框架,然后
用纸板将6个面包起来做一个正方体纸盒,至少需用
多少平方厘米纸板 这个纸盒的体积是多少立方厘米
第104页*综合练习*第7题
240÷12=20(厘米)
20×20×6=2400(平方厘米)
20×20×20=8000(立方厘米)
第104页*综合练习*第8题
8. 填一填。
长方体 长 宽 高 表面积 体积
1 8cm 5cm 4cm
2 18m 12m 7.5m
3 8.1dm 5dm 162dm3
184cm2
160cm3
882m2
1620m3
4dm
185.8dm2
第104页*综合练习*第9题
9. 一个集装箱长9米,宽3.2米,高2.5米。
(1) 制作这样一个集装箱至少需要多
少平方米的钢板
(9×3.2+9×2.5+3.2×2.5)×2=118.6(平方米)
第104页*综合练习*第9题
9. 一个集装箱长9米,宽3.2米,高2.5米。
(2) 这个集装箱的容积大约是多少立
方米 (箱壁厚度忽略不计)
9×3.2×2.5 = 72 (立方米)
第104页*综合练习*第10题
10. 一个长方体,如果高增加3厘米就变成棱长为8厘米的
正方体。原长方体的体积是多少
8×8×(8-3) = 320 (立方厘米)
聪明小屋
右图是由若干个棱长1厘米的小正方体拼成的,它的表面积和体积各是多少
表面积:6×6×2+ 6× 4× 4 = 168 (平方厘米)
体积:6×6×4- 1× 1× 4 = 140 (立方厘米)
我学会了吗?
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
(1) 建造这个游泳池需要挖土多少立方米
50×25×2.2 = 2750 (立方米)
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
(2) 要在它的四壁和底面铺上瓷砖,铺瓷砖部分的面积
是多少平方米
50×25+50×2.2×2+25×2.2×2 = 1580 (平方米)
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
(3) 如果要给这个游泳池注1.8米深的水,已知每小时能
注水150立方米,需用多少小时
50×25×1.8÷150 = 15 (小时)
上图是雅典奥林匹克水上运动中心的主游泳池,它的长是50米,宽是25米,深是2.2米。
(4) 你还能提出什么问题
(答案不唯一)这个游泳池的底面积是多少平方米?
有趣的溶解现象
将一石块放入水中,石块的体积加上水的体积······
把盐放入水中溶解后就变成了盐水。
盐水的体积=水的体积+盐的体积,对不对
设计个实验验证一下吧。
制订方案
我来设计实验方案。
(1) 取适量的水和盐,想办法分别测量并计算出它们的
体积。
(2) 将盐倒入水中,用玻璃棒搅拌至完全溶解,形成盐
水。测量并计算出盐水的体积。
(3) 比较水和盐的体积之和与盐水的体积是否相等。
实践探究
将盐倒入水中,用玻璃棒搅拌到完全溶解。
我是测量员······
我是记录员······
第_____小组探究记录表
水的体积 盐的体积 盐水的体积
交流展示
全班探究记录汇总表
小组 水的体积 盐的体积 盐水的体积
第一小组
第二小组
第三小组
······
结论
实验报告
实验目的:____________
_____________________
实验方法步骤:________
_____________________
实验结论:____________
_____________________
要让盐完全溶解,测量时要尽量减少误差。
实验报告
实验目的:____________
_____________________
实验方法步骤:________
_____________________
实验结论:____________
_____________________
通过实验,我们发现······
实验报告
实验目的:____________
_____________________
实验方法步骤:________
_____________________
实验结论:____________
_____________________
根据实验和查阅的资料,我写出了实验报告······
总结反思
只凭一次实验不能马上得出结论,汇总各个小组的实验结果才能得出结论。
为什么会产生这样的现象呢 把糖放入水中,会不会也有类似的现象呢
我们查一查资料,看有没有溶解后总体积增加的现象。
这次数学实践活动我用到的数学知识有······
课后作业
