1.2.1 直角三角形的判定(HL)同步练习(含解析)2022-2023学年北师大版八年级数学上册
文档属性
| 名称 | 1.2.1 直角三角形的判定(HL)同步练习(含解析)2022-2023学年北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 447.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 16:02:45 | ||
图片预览

文档简介
北师大版八年级数学 1.2.1 直角三角形的判定(HL)
一、单选题
1.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充的条件是( )
A.AC=AD或BC=BD B.AC=AD且BC=BD
C.∠BAC=∠BAD D.以上都不对
2.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角中,则的度数是( )
A.32° B.62° C.58° D.68°
3.用三角尺可按下面方法画角的平分线.如图,在两边上,分别取,再分别过点M,N作,的垂线,交点为P,画射线,可得.则判定三角形全等的依据是( )
A. B. C. D.
4.如图,在Rt△ABC中,,,在AC上取一点E,使,过点E作,连接CF,使,若,则AE的长为( )
A.5cm B.6cm C.7cm D.无法计算
5.如图,在△ABC中,,D是上一点,于点E,,连接,若,则等于( )
A.6 B.7 C.8 D.9
6.如图,,且,则判定≌的最好理由是( )
A. B. C. D.
7.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A.60° B.75° C.90° D.120°
8.如图,在中,,,为边上一点,于点.若,,则的长为( )
A. B.2 C. D.4
二、填空题
9.如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为 °.
10.如图,,请你添加一个条件 ,利用“”,证明.
11.如图,中,,点D在上,且于点E,,若,则 .
12.如图,D是内部一点,于E,于F,且,点B是射线上一点,,,在射线上取一点C,使得,则的长为 .
13.如图,在△ABC中,AD⊥BC于点D,AD与BE相交于点F,且AC=BF,DF=DC.若∠ABE=10°,则∠DBF的度数为 .
14.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP= 时,△ABC≌△QPA
三、解答题
15.如图,已知 ,点P在 上, , ,垂足分别为D,E.求证: .
16.如图,已知平分,于点E,于点F,且.求证:.
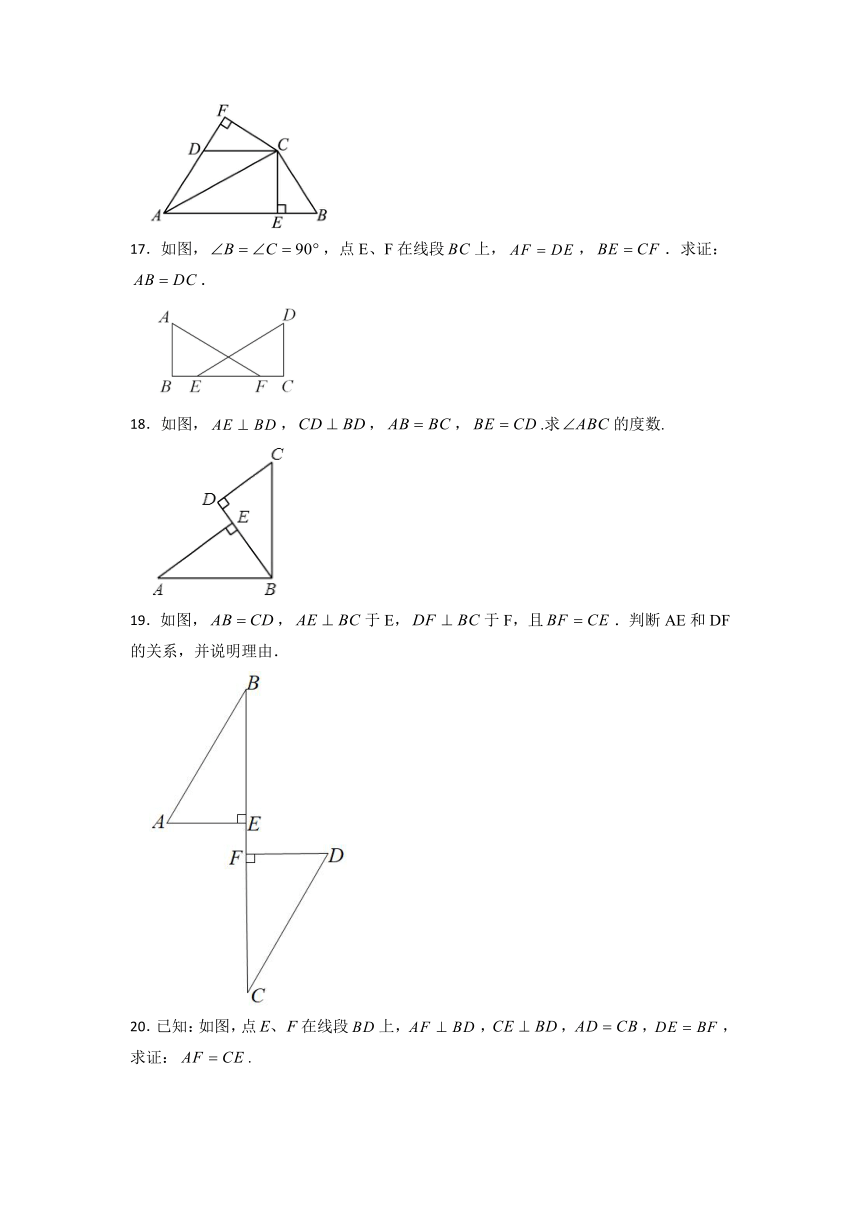
17.如图,,点E、F在线段上,,.求证:.
18.如图,,,,.求的度数.
19.如图,,于E,于F,且.判断AE和DF的关系,并说明理由.
20.已知:如图,点在线段上,,,,,求证:.
答案解析部分
1.【答案】A
【解析】【解答】解:在Rt△ABC与Rt△ABD中,
,
∴Rt△ABC≌Rt△ABD(HL),
在Rt△ABC与Rt△ABD中,
,
∴Rt△ABC≌Rt△ABD(HL),
故答案为:A.
【分析】根据“HL”得出添加AC=AD或BC=BD,再结合隐含的条件AB=AB,证出Rt△ABC≌Rt△ABD,即可得出答案.
2.【答案】C
【解析】【解答】解:在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠DEF=∠ABC=32°,
∴∠DFE=90°﹣32°=58°.
故答案为:C.
【分析】由题意根据HL定理可证Rt△ABC≌Rt△DEF,由全等三角形的对应角相等可得∠DEF=∠ABC,然后根据直角三角形两锐角互余可求解.
3.【答案】D
【解析】【解答】解:在和中,
,
∴(),
故答案为:D.
【分析】根据题干提供的信息可知Rt△OPM与Rt△OPN中,有一条直角边对应相等,且斜边是公共边,故利用HL可以判断Rt△OPM与Rt△OPN全等.
4.【答案】B
【解析】【解答】解:∵,
∴∠CEF=,
在Rt△ACB和Rt△FEC中,
,
∴Rt△ACB≌Rt△FEC,
∴AC=,EC=,
∴AE=AC-EC=6cm,
故答案为:B.
【分析】首先利用HL判断Rt△ACB≌Rt△FEC,根据全等三角形的对应边相等得AC=EF=10cm,进而根据AE=AC-EC进行计算即可.
5.【答案】C
【解析】【解答】解:∵,
∴,
∵,,
∴,
∴,
∴=8.
故答案为:C.
【分析】先证出,得出,即可得出=8.
6.【答案】D
【解析】【解答】解:,
,
在和中,,
和.
故答案为:D.
【分析】根据垂直的概念可得∠ADB=∠ADC=90°,由已知条件可知AB=AC,由图形可得AD=AD,然后根据全等三角形的判定定理进行解答.
7.【答案】C
【解析】【解答】解:∠ABC+∠DFE=90°,理由如下:
由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
故答案为:C.
【分析】由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF,证明Rt△ABC≌Rt△DEF,得到∠ABC=∠DEF,然后结合∠DEF+∠DFE=90°进行解答.
8.【答案】D
【解析】【解答】解:如图,作DF⊥AB于点F,
∵ AD=BD
∴△ADB是等腰三角形,∠ABD=∠A=40°
∴AB=2AF=2BF
∵,,
∴∠ABC=180°-∠A-∠C=80°,
∴ ∠DBE=∠ABC-∠ABD=40°
∴∠DBE=∠ABD
∵
∴ ∠DE=DF
∵BD=BD
∴Rt△BDF≌Rt△BDE(HL)
∴BF=BE=2
∴AB=2BF=4
故答案为:D
【分析】作DF⊥AB于点F,先利用“HL”证明Rt△BDF≌Rt△BDE可得BF=BE=2,再结合AB=2AF=2BF可得答案。
9.【答案】35
【解析】【解答】解:∵滑梯、墙、地面正好构成直角三角形,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ACB=∠DFE=55°,
∵∠ABC+∠BCA=90°,
∴∠ABC=90°﹣55°=35°.
故答案为:35.
【分析】首先利用HL判断Rt△ABC≌Rt△DEF,根据全等三角形的对应角相等得∠ACB=∠DFE=55°,进而根据直角三角形两锐角互余即可算出答案.
10.【答案】或
【解析】【解答】解:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等.
由图可知:和斜边为公共边,即,
∴应添加:或,
故答案为:或.
【分析】如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等,据此解答.
11.【答案】2.5
【解析】【解答】解:∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ .
故答案为: .
【分析】根据HL证明Rt△ACD≌Rt△AED,可得DE=CD=1.5,利用BD=BC-CD即可求解.
12.【答案】6或10
【解析】【解答】解: ①如图1,当点C在线段上时,连接,
∵于E,于F,
∴,
在和中,,
∴,
∴,
又∵在和中,,
∴,
∴,
∴;
②如图2,当点C在线段的延长线上时,
同理可得,,
∴.
故答案为:6或10.
【分析】 ①当点C在线段AF上时,连接AD,由垂直的概念可得∠DEB=∠DFC=90°,利用HL证明△DEB≌△DFC、△DEA≌△DFA,得到CF=BE=2,AF=AE=AB+BE=8,然后根据AC=AF-CF进行计算;②当点C在线段AF的延长线上时,同理求解即可.
13.【答案】35
【解析】【解答】解:,
,
在和中,
,
,
,
,
,
.
故答案为:35 .
【分析】先利用“HL”证明,可得AD=BD,,再结合∠ABE=10°,可得。
14.【答案】5
【解析】【解答】解:当AP=5时,△ABC≌△QPA,理由如下:
∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
当AP=5=BC时,
在Rt△ABC和Rt△QPA中
∴Rt△ABC≌Rt△QPA(HL).
【分析】利用全等三角形的性质求解即可。
15.【答案】证明:∵ ,
∴ 为 的角平分线,
又∵点P在 上, , ,
∴ , ,
又∵ (公共边),
∴ .
【解析】【分析】利用“HL”证明即可。
16.【答案】证明:∵平分,于,于,
∴,
在和中,
,
∴.
【解析】【分析】先利用角平分线的性质可得,再利用“HL”证明即可。
17.【答案】证明:∵,
∴,
∴,
在和中,
,
∴,
∴.
【解析】【分析】先证明BF=CE,再利用“HL”证明,可得。
18.【答案】解:∵,,
∴,
在和中
∵,
∴,
∴,
∵,
∴,
∴.
【解析】【分析】根据垂直的概念可得∠AEB=∠BDC=90°,利用HL证明Rt△AEB≌Rt△BDC,得到∠A=∠CBD,由余角的性质可得∠A+∠ABE=90°,则∠ABC=∠ABE+∠CBD=∠ABE+∠A,据此计算.
19.【答案】证明:∵AE⊥BC,DF⊥BC,
∴∠DFC =∠DFE=90°,∠AEB=∠AEF= 90°,
∴∠DFE=∠AEF
∴AE∥DF
又∵ CE= BF,
∴CE- EF= BF- EF,即CF= BE,
在Rt△DFC和Rt△AEB中,
∴Rt△DFC≌Rt△AEB (HL),
∴AE= DF.
所以AE∥DF,且AE=DF.
【解析】【分析】先求出∠DFE=∠AEF,可得AE//DF,再利用“HL”证明Rt△DFC≌Rt△AEB,然后利用全等三角形的性质可得AE=DF, 即可得到AE∥DF,且AE=DF。
20.【答案】证明:∵DE=BF,
∴DE+EF=BF+EF,
∴DF=BE,
在Rt△ADF和Rt△CBE中,
,
∴Rt△ADF≌Rt△CBE(HL),
∴AF=CE.
【解析】【分析】根据DE=BF结合线段的和差关系可得DF=BE,证明Rt△ADF≌Rt△CBE,据此可得结论.
一、单选题
1.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充的条件是( )
A.AC=AD或BC=BD B.AC=AD且BC=BD
C.∠BAC=∠BAD D.以上都不对
2.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角中,则的度数是( )
A.32° B.62° C.58° D.68°
3.用三角尺可按下面方法画角的平分线.如图,在两边上,分别取,再分别过点M,N作,的垂线,交点为P,画射线,可得.则判定三角形全等的依据是( )
A. B. C. D.
4.如图,在Rt△ABC中,,,在AC上取一点E,使,过点E作,连接CF,使,若,则AE的长为( )
A.5cm B.6cm C.7cm D.无法计算
5.如图,在△ABC中,,D是上一点,于点E,,连接,若,则等于( )
A.6 B.7 C.8 D.9
6.如图,,且,则判定≌的最好理由是( )
A. B. C. D.
7.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A.60° B.75° C.90° D.120°
8.如图,在中,,,为边上一点,于点.若,,则的长为( )
A. B.2 C. D.4
二、填空题
9.如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为 °.
10.如图,,请你添加一个条件 ,利用“”,证明.
11.如图,中,,点D在上,且于点E,,若,则 .
12.如图,D是内部一点,于E,于F,且,点B是射线上一点,,,在射线上取一点C,使得,则的长为 .
13.如图,在△ABC中,AD⊥BC于点D,AD与BE相交于点F,且AC=BF,DF=DC.若∠ABE=10°,则∠DBF的度数为 .
14.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP= 时,△ABC≌△QPA
三、解答题
15.如图,已知 ,点P在 上, , ,垂足分别为D,E.求证: .
16.如图,已知平分,于点E,于点F,且.求证:.
17.如图,,点E、F在线段上,,.求证:.
18.如图,,,,.求的度数.
19.如图,,于E,于F,且.判断AE和DF的关系,并说明理由.
20.已知:如图,点在线段上,,,,,求证:.
答案解析部分
1.【答案】A
【解析】【解答】解:在Rt△ABC与Rt△ABD中,
,
∴Rt△ABC≌Rt△ABD(HL),
在Rt△ABC与Rt△ABD中,
,
∴Rt△ABC≌Rt△ABD(HL),
故答案为:A.
【分析】根据“HL”得出添加AC=AD或BC=BD,再结合隐含的条件AB=AB,证出Rt△ABC≌Rt△ABD,即可得出答案.
2.【答案】C
【解析】【解答】解:在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠DEF=∠ABC=32°,
∴∠DFE=90°﹣32°=58°.
故答案为:C.
【分析】由题意根据HL定理可证Rt△ABC≌Rt△DEF,由全等三角形的对应角相等可得∠DEF=∠ABC,然后根据直角三角形两锐角互余可求解.
3.【答案】D
【解析】【解答】解:在和中,
,
∴(),
故答案为:D.
【分析】根据题干提供的信息可知Rt△OPM与Rt△OPN中,有一条直角边对应相等,且斜边是公共边,故利用HL可以判断Rt△OPM与Rt△OPN全等.
4.【答案】B
【解析】【解答】解:∵,
∴∠CEF=,
在Rt△ACB和Rt△FEC中,
,
∴Rt△ACB≌Rt△FEC,
∴AC=,EC=,
∴AE=AC-EC=6cm,
故答案为:B.
【分析】首先利用HL判断Rt△ACB≌Rt△FEC,根据全等三角形的对应边相等得AC=EF=10cm,进而根据AE=AC-EC进行计算即可.
5.【答案】C
【解析】【解答】解:∵,
∴,
∵,,
∴,
∴,
∴=8.
故答案为:C.
【分析】先证出,得出,即可得出=8.
6.【答案】D
【解析】【解答】解:,
,
在和中,,
和.
故答案为:D.
【分析】根据垂直的概念可得∠ADB=∠ADC=90°,由已知条件可知AB=AC,由图形可得AD=AD,然后根据全等三角形的判定定理进行解答.
7.【答案】C
【解析】【解答】解:∠ABC+∠DFE=90°,理由如下:
由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
故答案为:C.
【分析】由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF,证明Rt△ABC≌Rt△DEF,得到∠ABC=∠DEF,然后结合∠DEF+∠DFE=90°进行解答.
8.【答案】D
【解析】【解答】解:如图,作DF⊥AB于点F,
∵ AD=BD
∴△ADB是等腰三角形,∠ABD=∠A=40°
∴AB=2AF=2BF
∵,,
∴∠ABC=180°-∠A-∠C=80°,
∴ ∠DBE=∠ABC-∠ABD=40°
∴∠DBE=∠ABD
∵
∴ ∠DE=DF
∵BD=BD
∴Rt△BDF≌Rt△BDE(HL)
∴BF=BE=2
∴AB=2BF=4
故答案为:D
【分析】作DF⊥AB于点F,先利用“HL”证明Rt△BDF≌Rt△BDE可得BF=BE=2,再结合AB=2AF=2BF可得答案。
9.【答案】35
【解析】【解答】解:∵滑梯、墙、地面正好构成直角三角形,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ACB=∠DFE=55°,
∵∠ABC+∠BCA=90°,
∴∠ABC=90°﹣55°=35°.
故答案为:35.
【分析】首先利用HL判断Rt△ABC≌Rt△DEF,根据全等三角形的对应角相等得∠ACB=∠DFE=55°,进而根据直角三角形两锐角互余即可算出答案.
10.【答案】或
【解析】【解答】解:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等.
由图可知:和斜边为公共边,即,
∴应添加:或,
故答案为:或.
【分析】如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等,据此解答.
11.【答案】2.5
【解析】【解答】解:∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ .
故答案为: .
【分析】根据HL证明Rt△ACD≌Rt△AED,可得DE=CD=1.5,利用BD=BC-CD即可求解.
12.【答案】6或10
【解析】【解答】解: ①如图1,当点C在线段上时,连接,
∵于E,于F,
∴,
在和中,,
∴,
∴,
又∵在和中,,
∴,
∴,
∴;
②如图2,当点C在线段的延长线上时,
同理可得,,
∴.
故答案为:6或10.
【分析】 ①当点C在线段AF上时,连接AD,由垂直的概念可得∠DEB=∠DFC=90°,利用HL证明△DEB≌△DFC、△DEA≌△DFA,得到CF=BE=2,AF=AE=AB+BE=8,然后根据AC=AF-CF进行计算;②当点C在线段AF的延长线上时,同理求解即可.
13.【答案】35
【解析】【解答】解:,
,
在和中,
,
,
,
,
,
.
故答案为:35 .
【分析】先利用“HL”证明,可得AD=BD,,再结合∠ABE=10°,可得。
14.【答案】5
【解析】【解答】解:当AP=5时,△ABC≌△QPA,理由如下:
∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
当AP=5=BC时,
在Rt△ABC和Rt△QPA中
∴Rt△ABC≌Rt△QPA(HL).
【分析】利用全等三角形的性质求解即可。
15.【答案】证明:∵ ,
∴ 为 的角平分线,
又∵点P在 上, , ,
∴ , ,
又∵ (公共边),
∴ .
【解析】【分析】利用“HL”证明即可。
16.【答案】证明:∵平分,于,于,
∴,
在和中,
,
∴.
【解析】【分析】先利用角平分线的性质可得,再利用“HL”证明即可。
17.【答案】证明:∵,
∴,
∴,
在和中,
,
∴,
∴.
【解析】【分析】先证明BF=CE,再利用“HL”证明,可得。
18.【答案】解:∵,,
∴,
在和中
∵,
∴,
∴,
∵,
∴,
∴.
【解析】【分析】根据垂直的概念可得∠AEB=∠BDC=90°,利用HL证明Rt△AEB≌Rt△BDC,得到∠A=∠CBD,由余角的性质可得∠A+∠ABE=90°,则∠ABC=∠ABE+∠CBD=∠ABE+∠A,据此计算.
19.【答案】证明:∵AE⊥BC,DF⊥BC,
∴∠DFC =∠DFE=90°,∠AEB=∠AEF= 90°,
∴∠DFE=∠AEF
∴AE∥DF
又∵ CE= BF,
∴CE- EF= BF- EF,即CF= BE,
在Rt△DFC和Rt△AEB中,
∴Rt△DFC≌Rt△AEB (HL),
∴AE= DF.
所以AE∥DF,且AE=DF.
【解析】【分析】先求出∠DFE=∠AEF,可得AE//DF,再利用“HL”证明Rt△DFC≌Rt△AEB,然后利用全等三角形的性质可得AE=DF, 即可得到AE∥DF,且AE=DF。
20.【答案】证明:∵DE=BF,
∴DE+EF=BF+EF,
∴DF=BE,
在Rt△ADF和Rt△CBE中,
,
∴Rt△ADF≌Rt△CBE(HL),
∴AF=CE.
【解析】【分析】根据DE=BF结合线段的和差关系可得DF=BE,证明Rt△ADF≌Rt△CBE,据此可得结论.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
