18.1.1 (3)导学案
文档属性
| 名称 | 18.1.1 (3)导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 31.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-21 22:57:22 | ||
图片预览

文档简介
§18.1.1平行四边形的性质(第3课时)
*学习目标*:
1、理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2、能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
*学习重点*:平行四边形对角线互相平分的性质,以及性质的应用
*学习难点*:综合运用平行四边形的性质进行有关的论证和计算
学习过程:
一、[学前准备]
⒈你还记得什么是平行四边形
我们已经学过平行四边形的那些性质 这些性质你能用符号语言如何表示 ①对边性质:
符号语言:
②对角、邻角性质:
符号语言:
⒉如图1在ABCD 中,AD=40,CD=30,∠B=60°,
则BC= ______; AB=______; ∠A=______ , ∠C=_______, ∠D=
( 图1 ) ( 图2 )
⒊自学课本P43—44面内容, 在有疑惑的地方作好标记.
二、[自学 合作 探究] (请你先自己完成,并力争独立发现规律,再与小组讨论方法)
⒈如图2的平行四边形ABCD中有几对全等三角形 如何证明:
⒉你能发现OA与OC、OD与OB有怎样的关系吗 ABCD是中心对称图形吗 为什么
⒊归纳:平行四边形的性质:平行四边形的对角线_________________。平行四边形是 图形, 是对称中心.
符合语言:
三、[交流探索]
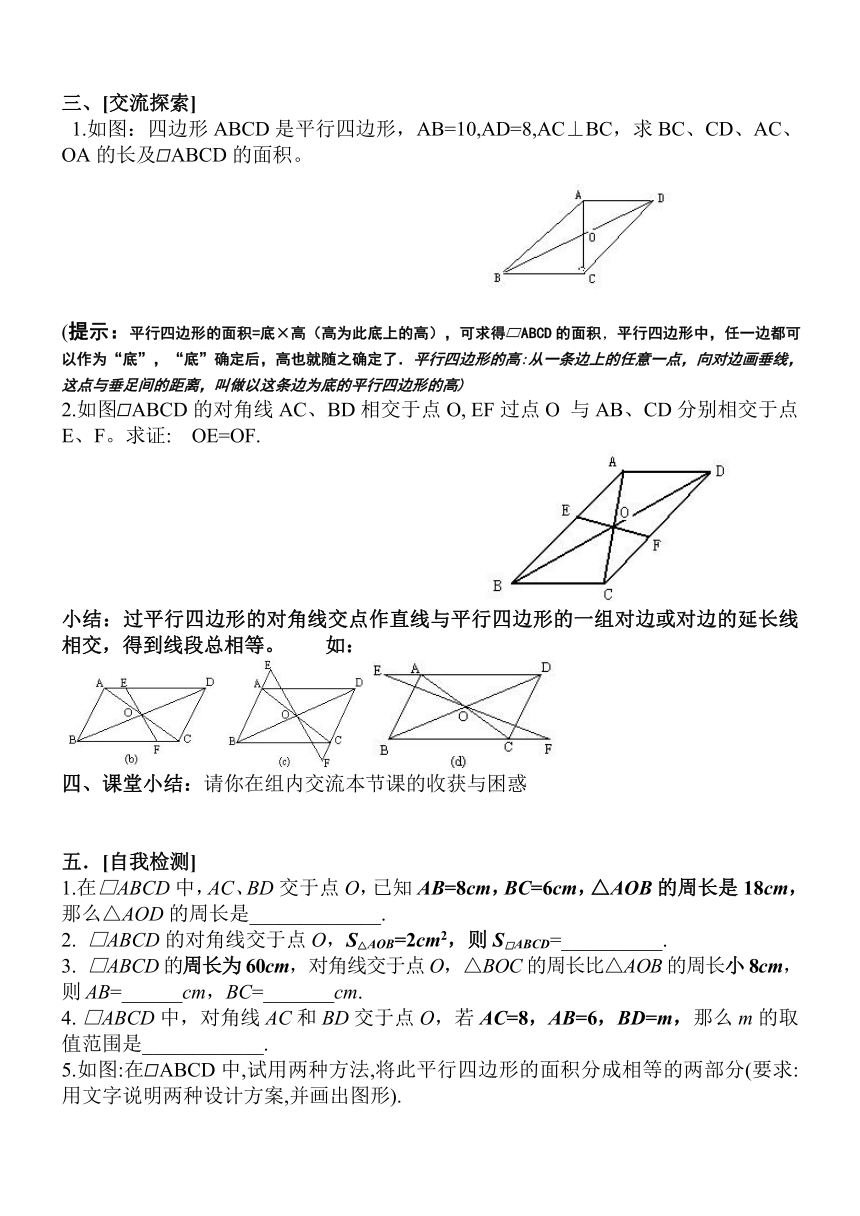
1.如图:四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长及ABCD的面积。
(提示:平行四边形的面积=底×高(高为此底上的高),可求得ABCD的面积,平行四边形中,任一边都可以作为“底”,“底”确定后,高也就随之确定了.平行四边形的高:从一条边上的任意一点,向对边画垂线,这点与垂足间的距离,叫做以这条边为底的平行四边形的高)
2.如图ABCD的对角线AC、BD相交于点O, EF过点O 与AB、CD分别相交于点E、F。求证: OE=OF.
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。 如:
四、课堂小结:请你在组内交流本节课的收获与困惑
五.[自我检测]
1.在□ABCD中,AC、BD交于点O,已知AB=8cm,BC=6cm,△AOB的周长是18cm,那么△AOD的周长是_____________.
2. □ABCD的对角线交于点O,S△AOB=2cm2,则S□ABCD=__________.
3. □ABCD的周长为60cm,对角线交于点O,△BOC的周长比△AOB的周长小8cm,则AB=______cm,BC=_______cm.
4. □ABCD中,对角线AC和BD交于点O,若AC=8,AB=6,BD=m,那么m的取值范围是____________.
5.如图:在ABCD中,试用两种方法,将此平行四边形的面积分成相等的两部分(要求:用文字说明两种设计方案,并画出图形).
引申:小明家有一块平行四边形菜地,菜地中间有一口井,为了浇水的方便,小明建议妈妈经过水井修一条路,可以把菜地分成面积相等的两部分. 同学们,你知道聪明的小明是怎么帮妈妈分的吗?
小结:过平行四边形对角线交点的任一条直线都将平行四边形分成面积相等的两部分
课后练习
1.判断对错
(1)在ABCD中,AC交BD于O,则AO=OB=OC=OD. ( )
(2)平行四边形两条对角线的交点到一组对边的距离相等. ( )
(3)平行四边形的两组对边分别平行且相等. ( )
(4)平行四边形是轴对称图形. ( )
2.在 ABCD中,AC=6、BD=4,则AB的范围是__ ______.
3.在平行四边形ABCD中,已知AB、BC、CD三条边的长度分别为(x+3),(x-4)
和16,则这个四边形的周长是 .
4.公园有一片绿地,它的形状是平行四边形,绿地上要修
几条笔直的小路,如图,AB=15cm,AD=12cm,AC⊥BC,
求小路BC,CD,OC的长,并算出绿地的面积.
5. □ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.(用2种方法证明)
A
D
B
C
A
D
M
●
B
C
*学习目标*:
1、理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2、能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
*学习重点*:平行四边形对角线互相平分的性质,以及性质的应用
*学习难点*:综合运用平行四边形的性质进行有关的论证和计算
学习过程:
一、[学前准备]
⒈你还记得什么是平行四边形
我们已经学过平行四边形的那些性质 这些性质你能用符号语言如何表示 ①对边性质:
符号语言:
②对角、邻角性质:
符号语言:
⒉如图1在ABCD 中,AD=40,CD=30,∠B=60°,
则BC= ______; AB=______; ∠A=______ , ∠C=_______, ∠D=
( 图1 ) ( 图2 )
⒊自学课本P43—44面内容, 在有疑惑的地方作好标记.
二、[自学 合作 探究] (请你先自己完成,并力争独立发现规律,再与小组讨论方法)
⒈如图2的平行四边形ABCD中有几对全等三角形 如何证明:
⒉你能发现OA与OC、OD与OB有怎样的关系吗 ABCD是中心对称图形吗 为什么
⒊归纳:平行四边形的性质:平行四边形的对角线_________________。平行四边形是 图形, 是对称中心.
符合语言:
三、[交流探索]
1.如图:四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长及ABCD的面积。
(提示:平行四边形的面积=底×高(高为此底上的高),可求得ABCD的面积,平行四边形中,任一边都可以作为“底”,“底”确定后,高也就随之确定了.平行四边形的高:从一条边上的任意一点,向对边画垂线,这点与垂足间的距离,叫做以这条边为底的平行四边形的高)
2.如图ABCD的对角线AC、BD相交于点O, EF过点O 与AB、CD分别相交于点E、F。求证: OE=OF.
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。 如:
四、课堂小结:请你在组内交流本节课的收获与困惑
五.[自我检测]
1.在□ABCD中,AC、BD交于点O,已知AB=8cm,BC=6cm,△AOB的周长是18cm,那么△AOD的周长是_____________.
2. □ABCD的对角线交于点O,S△AOB=2cm2,则S□ABCD=__________.
3. □ABCD的周长为60cm,对角线交于点O,△BOC的周长比△AOB的周长小8cm,则AB=______cm,BC=_______cm.
4. □ABCD中,对角线AC和BD交于点O,若AC=8,AB=6,BD=m,那么m的取值范围是____________.
5.如图:在ABCD中,试用两种方法,将此平行四边形的面积分成相等的两部分(要求:用文字说明两种设计方案,并画出图形).
引申:小明家有一块平行四边形菜地,菜地中间有一口井,为了浇水的方便,小明建议妈妈经过水井修一条路,可以把菜地分成面积相等的两部分. 同学们,你知道聪明的小明是怎么帮妈妈分的吗?
小结:过平行四边形对角线交点的任一条直线都将平行四边形分成面积相等的两部分
课后练习
1.判断对错
(1)在ABCD中,AC交BD于O,则AO=OB=OC=OD. ( )
(2)平行四边形两条对角线的交点到一组对边的距离相等. ( )
(3)平行四边形的两组对边分别平行且相等. ( )
(4)平行四边形是轴对称图形. ( )
2.在 ABCD中,AC=6、BD=4,则AB的范围是__ ______.
3.在平行四边形ABCD中,已知AB、BC、CD三条边的长度分别为(x+3),(x-4)
和16,则这个四边形的周长是 .
4.公园有一片绿地,它的形状是平行四边形,绿地上要修
几条笔直的小路,如图,AB=15cm,AD=12cm,AC⊥BC,
求小路BC,CD,OC的长,并算出绿地的面积.
5. □ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.(用2种方法证明)
A
D
B
C
A
D
M
●
B
C
