人教版三年级上册数学第八单元 分数的初步认识复习(综合复习)
文档属性
| 名称 | 人教版三年级上册数学第八单元 分数的初步认识复习(综合复习) |

|
|
| 格式 | docx | ||
| 文件大小 | 492.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 00:00:00 | ||
图片预览



文档简介
知识精讲
一.认识分数
1.几分之一的意义:把一个物体或图形平均分成若干份,其中的1份就用几分之一来表示.“平均分”是得到一个分数的必要前提.
2.分数的各部分名称:在分数中,分数中间的横线叫作分数线,分数线上面的数字叫作分子,分数线下面的数字叫作分母.
3.几分之一的读法:先读分母,再读分子,如,读作:二分之一.
4.几分之一的写法:先写分数线,再写分母,最后写分子.
5.几分之几各部分的名称及意义:分母表示把一个物体或图形平均分成几份,分子表示取其中的份数,分数线表示平均分.
6.几分之几可以看成几个几分之一,如可以看成3个.
二.分数大小比较
1.分子是1的两个分数相比较,分母大的分数反而小,分母小的分数反而大.例如.
2.同分母分数相比较,分子大的分数比较大,分子小的分数比较小.
三.同分母分数的计算
1.同分母分数相加,分母不变,分子相加.
同分母分数相加,也可以把两个加数分别看作几个几分之一,一共有几个几分之一,和就是几分之几.
2.同分母分数相减,分母不变,分子相减.
同分母分数相减,先把被减数和减数分别看作几个几分之一,相减后还剩几个几分之一,差就是几分之几.
3.计算1减几分之几时,减数的分母是几,1就变成分母和分子都是几的分数,再根据分数的意义相减.
四.分数的简单应用
1.在分数中,可以把一个物体或图形看作一个整体,也可以把多个个体的组合看作一个整体.
2.用分数表示部分量是整体的几分之几时,首先确定整体,再确定整体被平均分成了几份,并把它作为分数的分母,最后确定各部分占的份数,并把安作为分数的分子.
(部分量占整体的几分之几)
3.求一个数的几分之一的方法:明确几分之几表示的意义,找出整体对应的量;用除法求出1份是多少,即这个数的几分之一是多少.
4.求一个数的几分之几的方法:明确几分之几表示的意义,找出整体对应的量;用除法求出1份是多少;用乘法求出几份是多少.
分数的认识
例题1、 我能填得准。
(1)把一个苹果( )切成四块,每块是这个苹果的( )分之( ),写作( )。
(2)把一根1米长的钢筋平均分成( )份,每份是它的。
(3)10个同学平均分一块蛋糕,每个同学分得这块蛋糕的( ),读作( )。
(4)写出分数的各部分名称。
例题2、 把一张纸平均分成6份,每份是它的_______,这样的5份是_______个,就是它的_______.
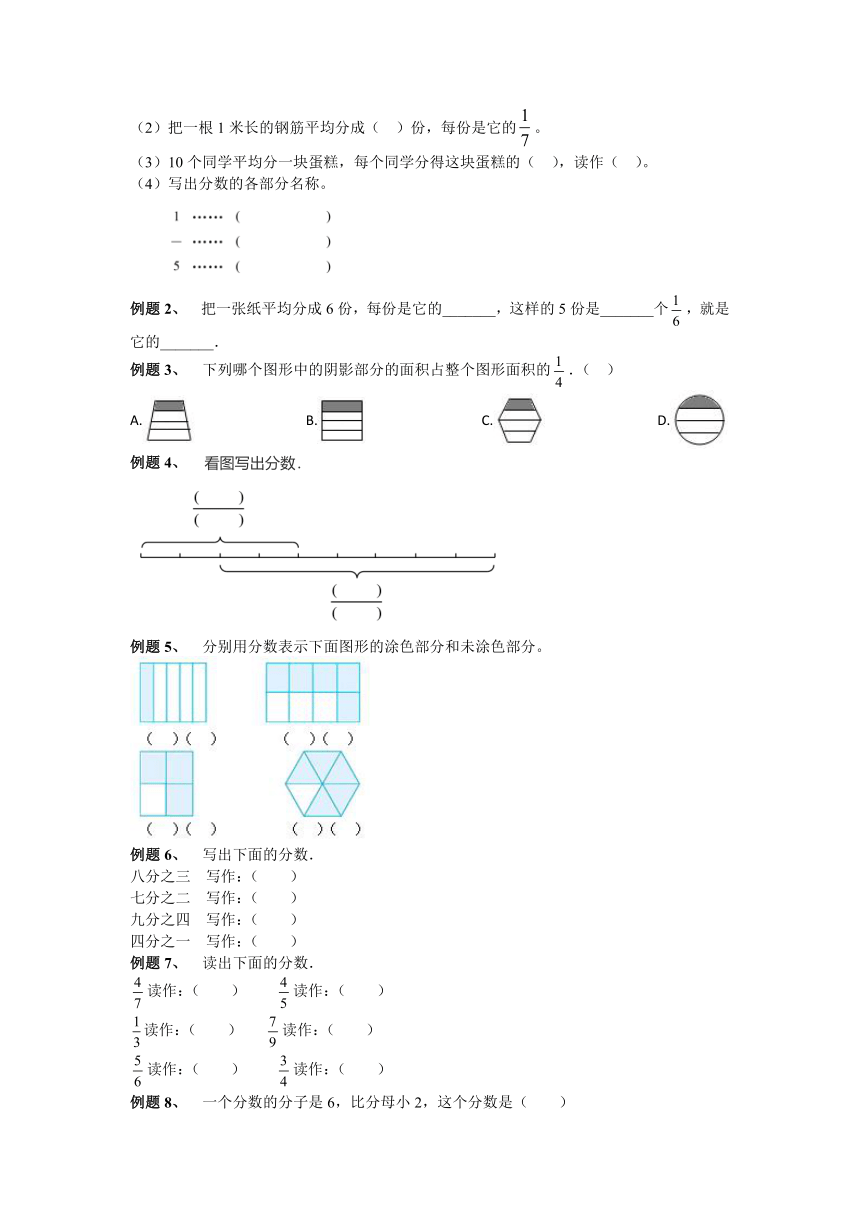
例题3、 下列哪个图形中的阴影部分的面积占整个图形面积的.( )
A. B. C. D.
例题4、 看图写出分数.
例题5、 分别用分数表示下面图形的涂色部分和未涂色部分。
例题6、 写出下面的分数.
八分之三 写作:( )
七分之二 写作:( )
九分之四 写作:( )
四分之一 写作:( )
例题7、 读出下面的分数.
读作:( ) 读作:( )
读作:( ) 读作:( )
读作:( ) 读作:( )
例题8、 一个分数的分子是6,比分母小2,这个分数是( )
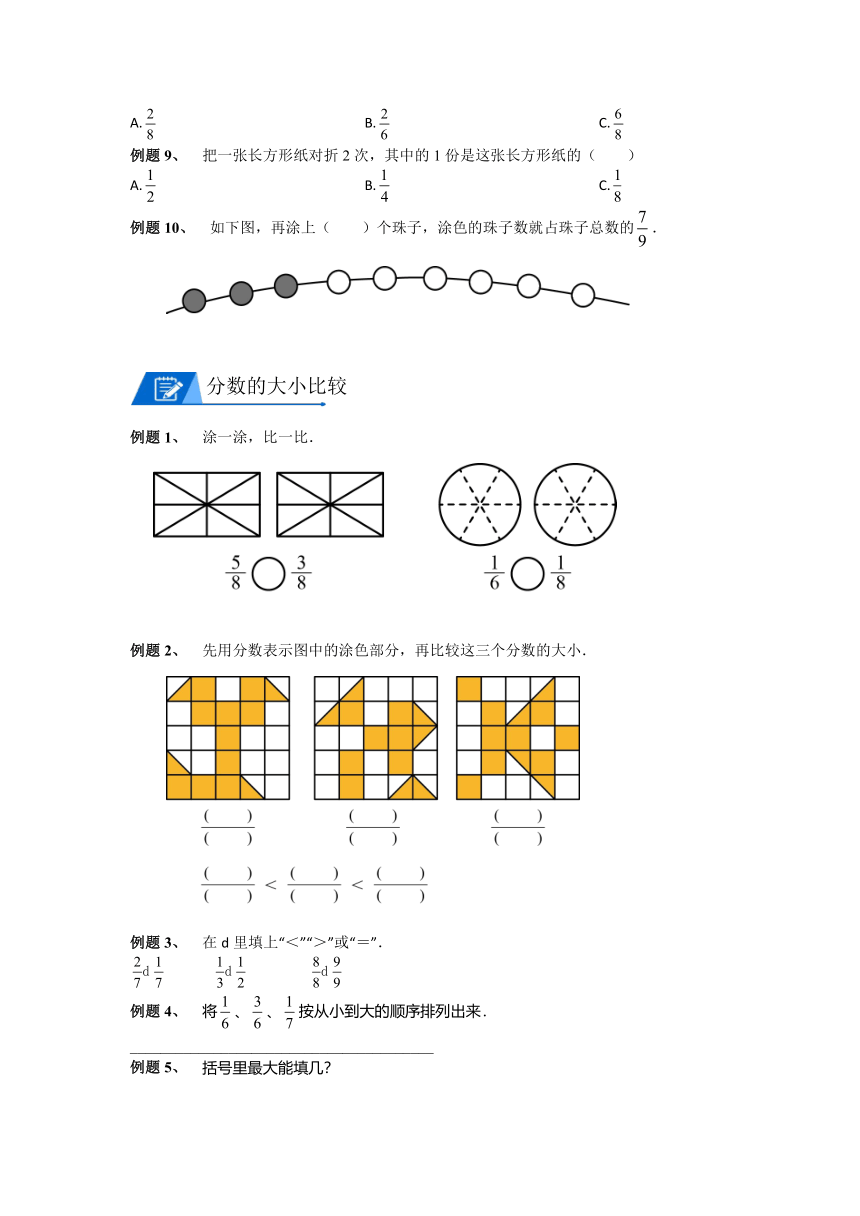
A. B. C.
例题9、 把一张长方形纸对折2次,其中的1份是这张长方形纸的( )
A. B. C.
例题10、 如下图,再涂上( )个珠子,涂色的珠子数就占珠子总数的.
分数的大小比较
例题1、 涂一涂,比一比.
例题2、 先用分数表示图中的涂色部分,再比较这三个分数的大小.
例题3、 在d里填上“<”“>”或“=”.
例题4、 将、、按从小到大的顺序排列出来.
________________________________________
例题5、 括号里最大能填几?
(1) (2) (3) (4)
例题6、 小丽用了一张纸的,小娟用了同样的一张纸的,谁用得多?画一画,比一比.
小丽:
小娟:
例题7、 盘子里有24条小鱼,猫妈妈吃了,猫宝宝吃了,谁吃得多?
分数计算
例题1、 就是________个,再加上4个,等于________个,也就是________.
例题2、 在计算时,可以先把1看作______个,再用______个减去______个,就是.
例题3、 口算
例题4、 ( )里最大能填几?
(1) (2) (3) (4)
例题5、 一块月饼平均分成9块,两人共吃了这个月饼的几分之几?
例题6、 小明看一本书,第一天看了这本书的,第二天看了这本书的,还剩这本书的几分之几没有看?
例题7、 妈妈买了一盒糖,一共有30块,把这盒糖的分给哥哥,剩下的分给弟弟,弟弟分得这盒糖的,弟弟比哥哥多分这盒糖的.
例题8、 一个大西瓜被平均切成8块,小熊吃了其中的2块。熊爸爸吃了以后,这个西瓜还剩。熊爸爸吃了这个西瓜的几分之几?
例题9、 一桶油,第一次倒了这桶油的,比第二次少倒了这桶油的.
(1)两次一共倒了这桶油的几分之几?
(2)还剩这桶油的几分之几?
分数的简单应用
例题1、 画一画.
(1)一盘草莓,小明吃了这盘草莓的,图中是剩下的,请把他吃了的草莓画出来.
(2)一盘桃子,小佳吃了这盘桃子的,还剩下4个桃子,请把她吃了的桃子画出来.
例题2、 有15颗糖,其中是巧克力糖,是水果糖.巧克力糖和水果糖各有多少颗?
答:巧克力糖有( )颗,水果糖有( )颗.
例题3、 一本书有120页,小强已经看了这本书的,还剩多少页没有看?
例题4、 18个苹果,拿出它的,平均分给3个小朋友,每人得( )个.
A.3 B.6 C.9
例题5、 比35的多9的数是( )
A.19 B.14 C.16 D.18
例题6、 盒子里有15块饼干,小红吃了,小林吃了,小红吃了______块,小林吃了______块.
例题7、 一盘鱼有12条,小花猫吃了这盘鱼的,小黑猫吃了这盘鱼的,小花猫和小黑猫各吃了多少条鱼?
例题8、 妈妈买来24粒巧克力,小明第一天吃了这些巧克力的,第二天吃了剩下的.小明第一天吃了________粒,第二天吃了________粒.
例题9、 一堆桃子,一共有50个。第一只猴子吃了它的,第二只猴子吃了剩下桃子的。
(1)这两只猴子哪只吃得多?
(2)还剩下多少个桃子没有吃?
答案解析
分数的认识
例题1、
【答案】 (1)平均四一(2)7(3)十分之一(4)分子分数线分母
【解析】 (1)平均四一(2)7(3)十分之一(4)分子分数线分母
例题2、
【答案】 ;5;
【解析】 把一张纸平均分成6份,每份是它的,这样的5份是5个,就是它的.
例题3、
【答案】 B
【解析】 因为A、C、D都不是平均分,只有B被平均分成了4部分,阴影部分的面积占整个图形面积的.
例题4、
【答案】
【解析】 把一条线段平均分成了9份,其中的1份是,上面括起来的部分包含4个,也就是,下面括起来的部分包含7个,也就是.
例题5、
【答案】 ;;;;;;;
【解析】 暂无解析
例题6、
【答案】
【解析】
例题7、
【答案】 七分之四 五分之四 三分之一 九分之七 六分之五 四分之三
【解析】 七分之四 五分之四 三分之一 九分之七 六分之五 四分之三
例题8、
【答案】 C
【解析】 6+2=8,
所以这个分数是.
例题9、
【答案】 B
【解析】 暂无解析
例题10、
【答案】 4
【解析】 4
分数的大小比较
例题1、
【答案】 涂一涂略>>
【解析】 涂一涂略>>
例题2、
【答案】
【解析】
例题3、
【答案】 >;<;=
【解析】
例题4、
【答案】
【解析】 暂无解析
例题5、
【答案】 4
【解析】 当分子是1时,分母大的分数反而小,分母小的反而大.(1)是,因此括号里填的数字应该比5小,能填1、2、3、4,最大能填4;同理,(2)的括号里最大能填7;(3)的括号里最大能填10;(4)的括号里最大能填12.
例题6、
【答案】 (画法不唯一)
>
【解析】 暂无解析
例题7、
【答案】 猫妈妈吃的多
【解析】 .
分数计算
例题1、
【答案】 3;7;1
【解析】 就是3个,再加上4个,等于7个,也就是1.
例题2、
【答案】 4,,4,,1,,
【解析】 在计算时,可以先把1看作4个,再用4个减去1个,就是.
例题3、
【答案】 ;;;;;;;
【解析】 暂无解析
例题4、
【答案】 6
【解析】 暂无解析
例题5、
【答案】
【解析】
例题6、
【答案】
【解析】
例题7、
【答案】 4
【解析】 解:;
答:弟弟分得这盒糖的,弟弟比哥哥多分这盒糖的.
例题8、
【答案】
【解析】
例题9、
【答案】 (1);(2)
【解析】 (1),
(2).
分数的简单应用
例题1、
【答案】 (1);(2)
【解析】 (1)把原来没吃之前的一盘草莓看成一个整体,剩下的占,就是把这个整体平均分成5份,剩余的是3份,图中剩余的草莓是3个,3份是3个,那么一份就是1个,原来所有的草莓有这样的5份,一共有5个草莓,所以需要再画2个草莓.
(2)小佳吃了这盘桃子的号,还剩,盘中还有4个桃子,所以剩下的是4个桃子,由此可知2个桃子为一份,3份是6个桃子,所以一共有6个桃子,需要再画2个桃子.
例题2、
【答案】 5 15÷3=5(颗) 涂色略
【解析】 5 15÷3=5(颗) 涂色略
例题3、
【答案】 120×(1-)=75(页)
【解析】 120×(1-)=75(页)
例题4、
【答案】 A
【解析】 解:(个)
答:每人得3个.
例题5、
【答案】 A
【解析】
例题6、
【答案】 5
【解析】 解:(块)
(块)
(块)
答:小红吃了5块,小林吃了10块.
例题7、
【答案】 3条;8条
【解析】 12÷4=3(条)
12÷3×2=8(条)
例题8、
【答案】 4
【解析】 解:(粒)
(粒)
答:小明第一天吃了4粒,第二天吃了5粒.
例题9、
【答案】 (1)第一只猴子:50÷5×2=20(个)第二只猴子:50-20=30(个) 30÷3×2=20(个) 20=20 一样多
(2)50-20-20=10(个)
【解析】 (1)第一只猴子:50÷5×2=20(个)第二只猴子:50-20=30(个) 30÷3×2=20(个) 20=20 一样多
(2)50-20-20=10(个)
一.认识分数
1.几分之一的意义:把一个物体或图形平均分成若干份,其中的1份就用几分之一来表示.“平均分”是得到一个分数的必要前提.
2.分数的各部分名称:在分数中,分数中间的横线叫作分数线,分数线上面的数字叫作分子,分数线下面的数字叫作分母.
3.几分之一的读法:先读分母,再读分子,如,读作:二分之一.
4.几分之一的写法:先写分数线,再写分母,最后写分子.
5.几分之几各部分的名称及意义:分母表示把一个物体或图形平均分成几份,分子表示取其中的份数,分数线表示平均分.
6.几分之几可以看成几个几分之一,如可以看成3个.
二.分数大小比较
1.分子是1的两个分数相比较,分母大的分数反而小,分母小的分数反而大.例如.
2.同分母分数相比较,分子大的分数比较大,分子小的分数比较小.
三.同分母分数的计算
1.同分母分数相加,分母不变,分子相加.
同分母分数相加,也可以把两个加数分别看作几个几分之一,一共有几个几分之一,和就是几分之几.
2.同分母分数相减,分母不变,分子相减.
同分母分数相减,先把被减数和减数分别看作几个几分之一,相减后还剩几个几分之一,差就是几分之几.
3.计算1减几分之几时,减数的分母是几,1就变成分母和分子都是几的分数,再根据分数的意义相减.
四.分数的简单应用
1.在分数中,可以把一个物体或图形看作一个整体,也可以把多个个体的组合看作一个整体.
2.用分数表示部分量是整体的几分之几时,首先确定整体,再确定整体被平均分成了几份,并把它作为分数的分母,最后确定各部分占的份数,并把安作为分数的分子.
(部分量占整体的几分之几)
3.求一个数的几分之一的方法:明确几分之几表示的意义,找出整体对应的量;用除法求出1份是多少,即这个数的几分之一是多少.
4.求一个数的几分之几的方法:明确几分之几表示的意义,找出整体对应的量;用除法求出1份是多少;用乘法求出几份是多少.
分数的认识
例题1、 我能填得准。
(1)把一个苹果( )切成四块,每块是这个苹果的( )分之( ),写作( )。
(2)把一根1米长的钢筋平均分成( )份,每份是它的。
(3)10个同学平均分一块蛋糕,每个同学分得这块蛋糕的( ),读作( )。
(4)写出分数的各部分名称。
例题2、 把一张纸平均分成6份,每份是它的_______,这样的5份是_______个,就是它的_______.
例题3、 下列哪个图形中的阴影部分的面积占整个图形面积的.( )
A. B. C. D.
例题4、 看图写出分数.
例题5、 分别用分数表示下面图形的涂色部分和未涂色部分。
例题6、 写出下面的分数.
八分之三 写作:( )
七分之二 写作:( )
九分之四 写作:( )
四分之一 写作:( )
例题7、 读出下面的分数.
读作:( ) 读作:( )
读作:( ) 读作:( )
读作:( ) 读作:( )
例题8、 一个分数的分子是6,比分母小2,这个分数是( )
A. B. C.
例题9、 把一张长方形纸对折2次,其中的1份是这张长方形纸的( )
A. B. C.
例题10、 如下图,再涂上( )个珠子,涂色的珠子数就占珠子总数的.
分数的大小比较
例题1、 涂一涂,比一比.
例题2、 先用分数表示图中的涂色部分,再比较这三个分数的大小.
例题3、 在d里填上“<”“>”或“=”.
例题4、 将、、按从小到大的顺序排列出来.
________________________________________
例题5、 括号里最大能填几?
(1) (2) (3) (4)
例题6、 小丽用了一张纸的,小娟用了同样的一张纸的,谁用得多?画一画,比一比.
小丽:
小娟:
例题7、 盘子里有24条小鱼,猫妈妈吃了,猫宝宝吃了,谁吃得多?
分数计算
例题1、 就是________个,再加上4个,等于________个,也就是________.
例题2、 在计算时,可以先把1看作______个,再用______个减去______个,就是.
例题3、 口算
例题4、 ( )里最大能填几?
(1) (2) (3) (4)
例题5、 一块月饼平均分成9块,两人共吃了这个月饼的几分之几?
例题6、 小明看一本书,第一天看了这本书的,第二天看了这本书的,还剩这本书的几分之几没有看?
例题7、 妈妈买了一盒糖,一共有30块,把这盒糖的分给哥哥,剩下的分给弟弟,弟弟分得这盒糖的,弟弟比哥哥多分这盒糖的.
例题8、 一个大西瓜被平均切成8块,小熊吃了其中的2块。熊爸爸吃了以后,这个西瓜还剩。熊爸爸吃了这个西瓜的几分之几?
例题9、 一桶油,第一次倒了这桶油的,比第二次少倒了这桶油的.
(1)两次一共倒了这桶油的几分之几?
(2)还剩这桶油的几分之几?
分数的简单应用
例题1、 画一画.
(1)一盘草莓,小明吃了这盘草莓的,图中是剩下的,请把他吃了的草莓画出来.
(2)一盘桃子,小佳吃了这盘桃子的,还剩下4个桃子,请把她吃了的桃子画出来.
例题2、 有15颗糖,其中是巧克力糖,是水果糖.巧克力糖和水果糖各有多少颗?
答:巧克力糖有( )颗,水果糖有( )颗.
例题3、 一本书有120页,小强已经看了这本书的,还剩多少页没有看?
例题4、 18个苹果,拿出它的,平均分给3个小朋友,每人得( )个.
A.3 B.6 C.9
例题5、 比35的多9的数是( )
A.19 B.14 C.16 D.18
例题6、 盒子里有15块饼干,小红吃了,小林吃了,小红吃了______块,小林吃了______块.
例题7、 一盘鱼有12条,小花猫吃了这盘鱼的,小黑猫吃了这盘鱼的,小花猫和小黑猫各吃了多少条鱼?
例题8、 妈妈买来24粒巧克力,小明第一天吃了这些巧克力的,第二天吃了剩下的.小明第一天吃了________粒,第二天吃了________粒.
例题9、 一堆桃子,一共有50个。第一只猴子吃了它的,第二只猴子吃了剩下桃子的。
(1)这两只猴子哪只吃得多?
(2)还剩下多少个桃子没有吃?
答案解析
分数的认识
例题1、
【答案】 (1)平均四一(2)7(3)十分之一(4)分子分数线分母
【解析】 (1)平均四一(2)7(3)十分之一(4)分子分数线分母
例题2、
【答案】 ;5;
【解析】 把一张纸平均分成6份,每份是它的,这样的5份是5个,就是它的.
例题3、
【答案】 B
【解析】 因为A、C、D都不是平均分,只有B被平均分成了4部分,阴影部分的面积占整个图形面积的.
例题4、
【答案】
【解析】 把一条线段平均分成了9份,其中的1份是,上面括起来的部分包含4个,也就是,下面括起来的部分包含7个,也就是.
例题5、
【答案】 ;;;;;;;
【解析】 暂无解析
例题6、
【答案】
【解析】
例题7、
【答案】 七分之四 五分之四 三分之一 九分之七 六分之五 四分之三
【解析】 七分之四 五分之四 三分之一 九分之七 六分之五 四分之三
例题8、
【答案】 C
【解析】 6+2=8,
所以这个分数是.
例题9、
【答案】 B
【解析】 暂无解析
例题10、
【答案】 4
【解析】 4
分数的大小比较
例题1、
【答案】 涂一涂略>>
【解析】 涂一涂略>>
例题2、
【答案】
【解析】
例题3、
【答案】 >;<;=
【解析】
例题4、
【答案】
【解析】 暂无解析
例题5、
【答案】 4
【解析】 当分子是1时,分母大的分数反而小,分母小的反而大.(1)是,因此括号里填的数字应该比5小,能填1、2、3、4,最大能填4;同理,(2)的括号里最大能填7;(3)的括号里最大能填10;(4)的括号里最大能填12.
例题6、
【答案】 (画法不唯一)
>
【解析】 暂无解析
例题7、
【答案】 猫妈妈吃的多
【解析】 .
分数计算
例题1、
【答案】 3;7;1
【解析】 就是3个,再加上4个,等于7个,也就是1.
例题2、
【答案】 4,,4,,1,,
【解析】 在计算时,可以先把1看作4个,再用4个减去1个,就是.
例题3、
【答案】 ;;;;;;;
【解析】 暂无解析
例题4、
【答案】 6
【解析】 暂无解析
例题5、
【答案】
【解析】
例题6、
【答案】
【解析】
例题7、
【答案】 4
【解析】 解:;
答:弟弟分得这盒糖的,弟弟比哥哥多分这盒糖的.
例题8、
【答案】
【解析】
例题9、
【答案】 (1);(2)
【解析】 (1),
(2).
分数的简单应用
例题1、
【答案】 (1);(2)
【解析】 (1)把原来没吃之前的一盘草莓看成一个整体,剩下的占,就是把这个整体平均分成5份,剩余的是3份,图中剩余的草莓是3个,3份是3个,那么一份就是1个,原来所有的草莓有这样的5份,一共有5个草莓,所以需要再画2个草莓.
(2)小佳吃了这盘桃子的号,还剩,盘中还有4个桃子,所以剩下的是4个桃子,由此可知2个桃子为一份,3份是6个桃子,所以一共有6个桃子,需要再画2个桃子.
例题2、
【答案】 5 15÷3=5(颗) 涂色略
【解析】 5 15÷3=5(颗) 涂色略
例题3、
【答案】 120×(1-)=75(页)
【解析】 120×(1-)=75(页)
例题4、
【答案】 A
【解析】 解:(个)
答:每人得3个.
例题5、
【答案】 A
【解析】
例题6、
【答案】 5
【解析】 解:(块)
(块)
(块)
答:小红吃了5块,小林吃了10块.
例题7、
【答案】 3条;8条
【解析】 12÷4=3(条)
12÷3×2=8(条)
例题8、
【答案】 4
【解析】 解:(粒)
(粒)
答:小明第一天吃了4粒,第二天吃了5粒.
例题9、
【答案】 (1)第一只猴子:50÷5×2=20(个)第二只猴子:50-20=30(个) 30÷3×2=20(个) 20=20 一样多
(2)50-20-20=10(个)
【解析】 (1)第一只猴子:50÷5×2=20(个)第二只猴子:50-20=30(个) 30÷3×2=20(个) 20=20 一样多
(2)50-20-20=10(个)
