18.1.1平行四边形的性质(1) 课件(共23张PPT)
文档属性
| 名称 | 18.1.1平行四边形的性质(1) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 11:43:59 | ||
图片预览





文档简介
(共23张PPT)
18.1.1平行四边形的性质
人教版八年级下册
1.掌握平行四边形的概念.
2.探索并熟练运用平行四边形的性质.
教学目标
新知导入
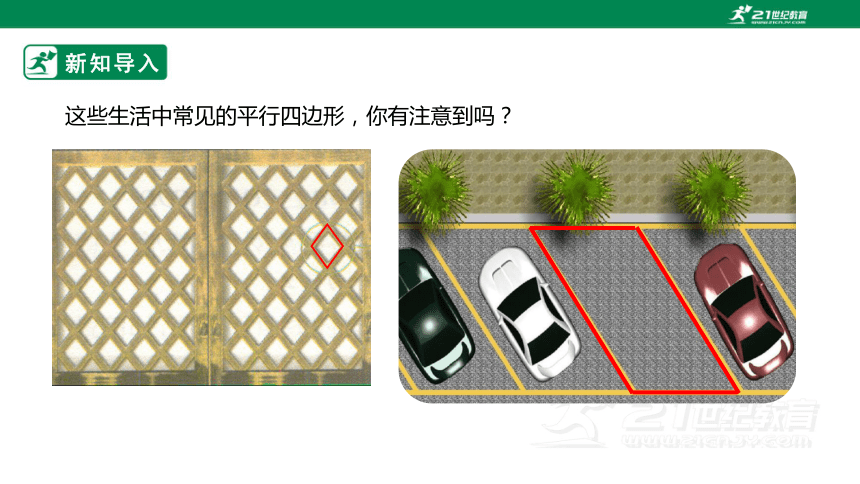
这些生活中常见的平行四边形,你有注意到吗?
新知导入
这些生活中常见的平行四边形,你有注意到吗?
新知探究
知识点 1
平行四边形的概念
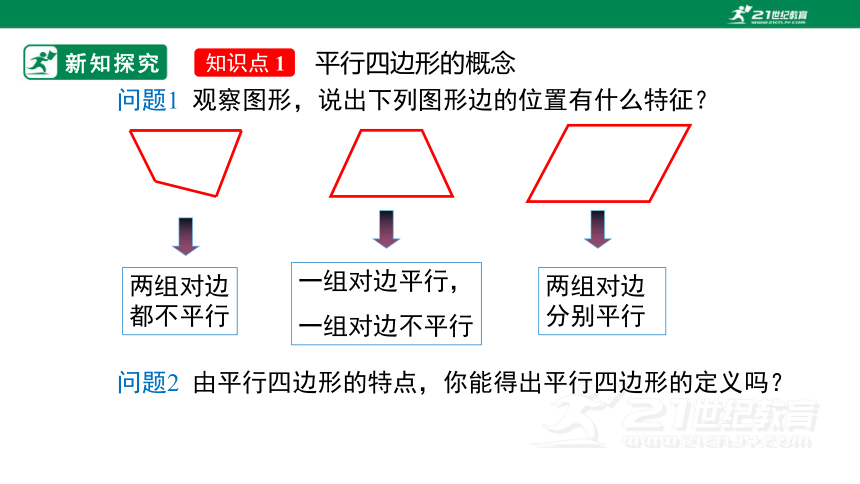
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
问题1 观察图形,说出下列图形边的位置有什么特征?
问题2 由平行四边形的特点,你能得出平行四边形的定义吗?
新知探究
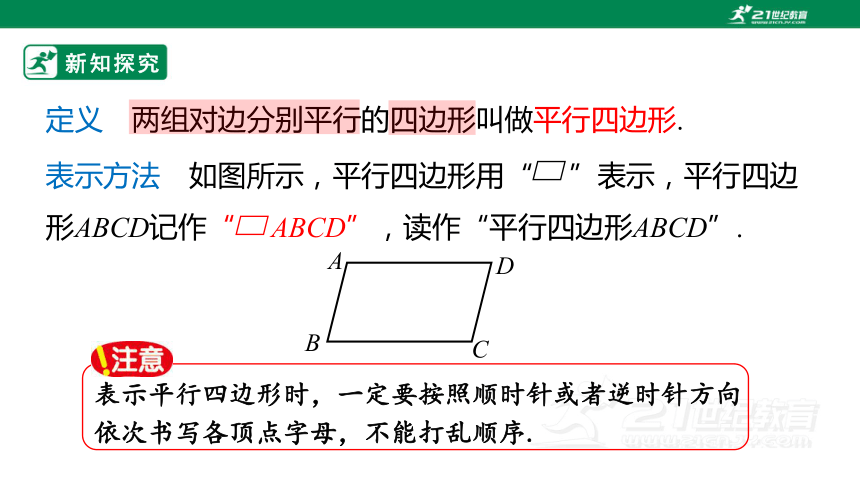
定义 两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
表示方法 如图所示,平行四边形用“ ”表示,平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD”.
表示平行四边形时,一定要按照顺时针或者逆时针方向依次书写各顶点字母,不能打乱顺序.
新知探究
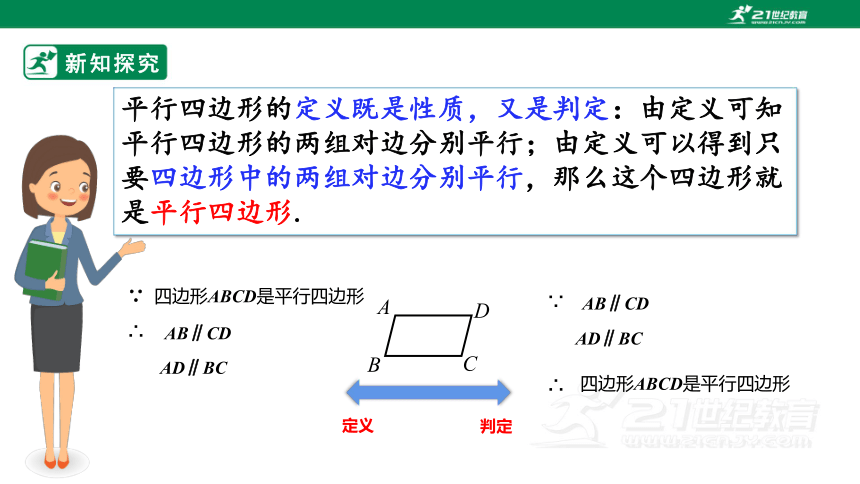
平行四边形的定义既是性质,又是判定:由定义可知平行四边形的两组对边分别平行;由定义可以得到只要四边形中的两组对边分别平行,那么这个四边形就是平行四边形.
AB∥CD
AD∥BC
∵
∵ 四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
A
B
C
D
四边形ABCD是平行四边形
∴
定义
判定
新知探究
如图,DC∥GH ∥ AB,DA∥ EF∥ CB,图中的
平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
解:∵DC∥GH ∥ AB,
DA∥ EF∥ CB,
∴根据平行四边形的定义可以判定图中共有9个平行四边形,即
AEKG, ABHG, AEFD, GKFD,
K
BEKH, CHKF, BEFC, CDGH, ABCD.
归纳:用定义判定平行四边形,即看四边形两组对边是否分别平行.
例1
新知练习
1.________________________叫做平行四边形.平行四边形ABCD记作_______.
2.平行四边形相对的边称为_______,相对的角称为______.
3.平行四边形的对边______,对角______.
4.两条平行线间的任何两条平行线段都________;平行线间的距离处处_______.
两组对边分别平行的四边形
对边
对角
相等
ABCD
相等
相等
相等
新知探究
知识点 2
平行四边形的性质
探究 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?它的角之间有什么关系?
A
B
C
D
新知探究
A
B
C
D
探究 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?它的角之间有什么关系?度量一下,和你的猜想一致吗?
猜想:对边相等,对角相等.
新知探究
例2 已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD.
教师点拨:
四边形的问题经常转化成三角形的问题求解,在平行四边形的基础上,利用相等的边和角构造全等三角形是证角、线段相等的常用方法.
证明:
连接AC
∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠1=∠3,∠2=∠4.
∵AC=AC
∴△ABC≌△CDA(ASA),∴AB=CD,CB=AD,∠B=∠D,
又∵∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4
∴∠BAD=∠BCD.
A
B
C
D
⌒
⌒
⌒
⌒
1
2
4
3
新知小结
A
B
C
D
性质1 平行四边形的对边相等.
数学语言 ∵四边形ABCD是平行四边形∴AD=BC,AB=CD.
性质2 平行四边形的对角相等.
数学语言 ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C , ∠B= ∠D.
A
B
C
D
新知探究
例3 如图,小明用一根36m的长绳子围成一个平行四边形的场地,其中一条边AB长为8m,其他三条边长各是多少?
教师点拨:
由平行四边形角、边之间的相等关系,可以解决角、边之间的有关计算问题.
解:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8m,∴CD=8m.
又AB+BC+CD+AD=36m,
∴AD=BC=10m.
新知练习
解:
教师点拨:
在平行四边形中,只要知道其中一个内角,其他内角可根据“对角相等或同旁内角互补”两性质求解.
在
5.如图,在 ABCD中,∠A+∠C=160°,求∠A、∠C、∠B、∠D的度数.
又∵∠A+∠C=160°,
∴∠A=∠C=80°
∵在
ABCD中, AD∥CB,
ABCD中,∠A=∠C,
∴∠A+∠B=180°,
∴∠B=∠D=180°-∠A=180°-80°=100°
新知探究
例4 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为
E,F. 求证:AE=CF.
证明: ∵四边形ABCD 是平行四边形
∴ ∠A= ∠C , AD=CB
∵ DE⊥AB,BF⊥CD
∴ ∠AED=∠CFB=90
∵ 在△ADE和△CBF中, ∠A= ∠C ,
∠AED=∠CFB,AD=CB.
∴△ADE≌△CBF (AAS),
∴ AE=CF.
新知练习
证明:
教师点拨:
本题综合考查了平行四边形的性质、全等三角形的判定与性质等.
∵AE=CF,
6.在平行四边形ABCD中,E、F是AC的两点,且AE=CF,求证:ED∥BF.
在平行四边形ABCD中,AB∥CD,AB=CD
∴∠BAC=∠DCA,
∴AE+EF=CF+EF,即AF=CE,
∴△ABF≌△CDE(SAS),
∴∠AFB=∠DEC,
∴ED∥BF.
课堂总结
平行四边形的性质
概念
性质
两组对边分别平行的四边形叫做平行四边形.
①对边相等
②对角相等
课堂练习
相等
相等
互补
C
C
课堂练习
4. 如图,在 ABCD中,AB=10,AD=8,AC⊥BC.求BC、CD、AC、OA的长,以及 ABCD的面积.
解: ∵四边形ABCD 是平行四边形
∴ BC=AD=8,CD=AB=10
∵ AC⊥BC ∴△ABC是直角三角形
根据勾股定理得:AC=
又OA=OC ∴OA=AC=3
∴平行四边形ABCD的面积=BC·AC=8×6=48.
课堂练习
解: ∵四边形ABCD是平行四边形, AD 6
∴BC AD6,
∵ AC⊥BC, AB=10
∴
∴
∴ BD 2OB
5. 在 ABCD中,AB=10, AD=6,AC⊥BC,则 BD 的长为多少?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
18.1.1平行四边形的性质
人教版八年级下册
1.掌握平行四边形的概念.
2.探索并熟练运用平行四边形的性质.
教学目标
新知导入
这些生活中常见的平行四边形,你有注意到吗?
新知导入
这些生活中常见的平行四边形,你有注意到吗?
新知探究
知识点 1
平行四边形的概念
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
问题1 观察图形,说出下列图形边的位置有什么特征?
问题2 由平行四边形的特点,你能得出平行四边形的定义吗?
新知探究
定义 两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
表示方法 如图所示,平行四边形用“ ”表示,平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD”.
表示平行四边形时,一定要按照顺时针或者逆时针方向依次书写各顶点字母,不能打乱顺序.
新知探究
平行四边形的定义既是性质,又是判定:由定义可知平行四边形的两组对边分别平行;由定义可以得到只要四边形中的两组对边分别平行,那么这个四边形就是平行四边形.
AB∥CD
AD∥BC
∵
∵ 四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
A
B
C
D
四边形ABCD是平行四边形
∴
定义
判定
新知探究
如图,DC∥GH ∥ AB,DA∥ EF∥ CB,图中的
平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
解:∵DC∥GH ∥ AB,
DA∥ EF∥ CB,
∴根据平行四边形的定义可以判定图中共有9个平行四边形,即
AEKG, ABHG, AEFD, GKFD,
K
BEKH, CHKF, BEFC, CDGH, ABCD.
归纳:用定义判定平行四边形,即看四边形两组对边是否分别平行.
例1
新知练习
1.________________________叫做平行四边形.平行四边形ABCD记作_______.
2.平行四边形相对的边称为_______,相对的角称为______.
3.平行四边形的对边______,对角______.
4.两条平行线间的任何两条平行线段都________;平行线间的距离处处_______.
两组对边分别平行的四边形
对边
对角
相等
ABCD
相等
相等
相等
新知探究
知识点 2
平行四边形的性质
探究 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?它的角之间有什么关系?
A
B
C
D
新知探究
A
B
C
D
探究 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?它的角之间有什么关系?度量一下,和你的猜想一致吗?
猜想:对边相等,对角相等.
新知探究
例2 已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD.
教师点拨:
四边形的问题经常转化成三角形的问题求解,在平行四边形的基础上,利用相等的边和角构造全等三角形是证角、线段相等的常用方法.
证明:
连接AC
∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠1=∠3,∠2=∠4.
∵AC=AC
∴△ABC≌△CDA(ASA),∴AB=CD,CB=AD,∠B=∠D,
又∵∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4
∴∠BAD=∠BCD.
A
B
C
D
⌒
⌒
⌒
⌒
1
2
4
3
新知小结
A
B
C
D
性质1 平行四边形的对边相等.
数学语言 ∵四边形ABCD是平行四边形∴AD=BC,AB=CD.
性质2 平行四边形的对角相等.
数学语言 ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C , ∠B= ∠D.
A
B
C
D
新知探究
例3 如图,小明用一根36m的长绳子围成一个平行四边形的场地,其中一条边AB长为8m,其他三条边长各是多少?
教师点拨:
由平行四边形角、边之间的相等关系,可以解决角、边之间的有关计算问题.
解:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8m,∴CD=8m.
又AB+BC+CD+AD=36m,
∴AD=BC=10m.
新知练习
解:
教师点拨:
在平行四边形中,只要知道其中一个内角,其他内角可根据“对角相等或同旁内角互补”两性质求解.
在
5.如图,在 ABCD中,∠A+∠C=160°,求∠A、∠C、∠B、∠D的度数.
又∵∠A+∠C=160°,
∴∠A=∠C=80°
∵在
ABCD中, AD∥CB,
ABCD中,∠A=∠C,
∴∠A+∠B=180°,
∴∠B=∠D=180°-∠A=180°-80°=100°
新知探究
例4 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为
E,F. 求证:AE=CF.
证明: ∵四边形ABCD 是平行四边形
∴ ∠A= ∠C , AD=CB
∵ DE⊥AB,BF⊥CD
∴ ∠AED=∠CFB=90
∵ 在△ADE和△CBF中, ∠A= ∠C ,
∠AED=∠CFB,AD=CB.
∴△ADE≌△CBF (AAS),
∴ AE=CF.
新知练习
证明:
教师点拨:
本题综合考查了平行四边形的性质、全等三角形的判定与性质等.
∵AE=CF,
6.在平行四边形ABCD中,E、F是AC的两点,且AE=CF,求证:ED∥BF.
在平行四边形ABCD中,AB∥CD,AB=CD
∴∠BAC=∠DCA,
∴AE+EF=CF+EF,即AF=CE,
∴△ABF≌△CDE(SAS),
∴∠AFB=∠DEC,
∴ED∥BF.
课堂总结
平行四边形的性质
概念
性质
两组对边分别平行的四边形叫做平行四边形.
①对边相等
②对角相等
课堂练习
相等
相等
互补
C
C
课堂练习
4. 如图,在 ABCD中,AB=10,AD=8,AC⊥BC.求BC、CD、AC、OA的长,以及 ABCD的面积.
解: ∵四边形ABCD 是平行四边形
∴ BC=AD=8,CD=AB=10
∵ AC⊥BC ∴△ABC是直角三角形
根据勾股定理得:AC=
又OA=OC ∴OA=AC=3
∴平行四边形ABCD的面积=BC·AC=8×6=48.
课堂练习
解: ∵四边形ABCD是平行四边形, AD 6
∴BC AD6,
∵ AC⊥BC, AB=10
∴
∴
∴ BD 2OB
5. 在 ABCD中,AB=10, AD=6,AC⊥BC,则 BD 的长为多少?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
