图形的运动(三)(单元测试)五年级下册数学人教版(带答案)
文档属性
| 名称 | 图形的运动(三)(单元测试)五年级下册数学人教版(带答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 526.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 00:00:00 | ||
图片预览


文档简介
人教版数学五年级下册图形的运动单元测试
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、选择题(共20分)
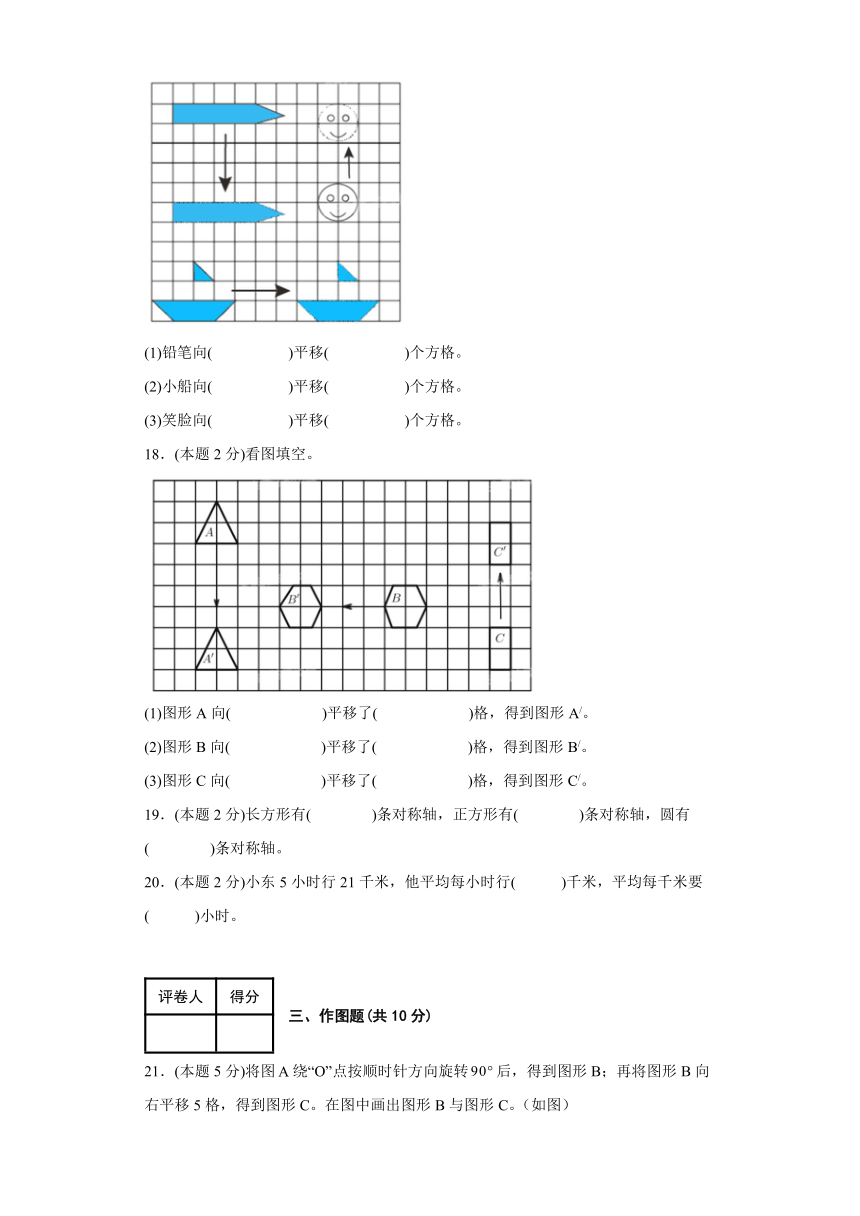
1.(本题2分)圆的对称轴有( )。
A.没有 B.1条 C.2条 D.无数条
2.(本题2分)如图中涂色部分是由空白部分绕点0顺时针旋转90°得到的是( )。
A. B. C. D.
3.(本题2分)把一个图形绕某个点旋转30°后,所得到的图形与原来的图形相比较,( )。
A.变大了 B.大小不变 C.变小了 D.无法确定大小是否变化
4.(本题2分)下列图形中,对称轴条数最多的是( )。
A.长方形 B.正方形 C.等边三角形 D.圆形
5.(本题2分)下图中阴影部分是由空白部分绕点O顺时针旋转90°后得到的是( )。
A. B. C.
6.(本题2分)教室门的打开和关闭,门的运动是( )现象。
A.平移 B.旋转 C.平移和旋转
7.(本题2分)下面说法正确的是( )。
A.旋转改变图形的形状和大小 B.平移改变图形的形状和大小
C.平移和旋转都不改变图形的形状和大小 D.A和B都对
8.(本题2分)从2里面每次减去,需要连续减( )次,结果是0。
A.2 B.6 C.9
9.(本题2分)--=-(+)应用了( )。
A.减法结合律 B.减法性质 C.加法结合律
10.(本题2分)某时刻钟表时针在10点到11点之间,此时刻再过6分钟后分针和此时刻3分钟前的时针正好方向相反且在一条直线上,则此时刻为( )。
A.10点15分 B.10点19分 C.10点20分 D.10点25分
评卷人得分
二、填空题(共20分)
11.(本题2分)如图,图形1绕点O顺时针旋转90°到图形( )所在的位置,图形4绕点O逆时针旋转90°到图形( )所在的位置,图形2绕点O顺时针旋转180°到图形( )所在的位置,图形2绕点O顺时针旋转( )到图形3所在的位置。
12.(本题2分)的分数单位是( ),它减去5个这样的单位,结果是( )。
13.(本题2分)从12:00到12:15,分针按( )时针方向旋转了( ) °。
14.(本题2分)从3点到4点,钟上的分针转了( )度,时针转了( )度。
15.(本题2分)指针从“12”绕点O顺时针旋转( ) °到“8”,再继续顺时针旋转( ) °到“9”。
16.(本题2分)回答下列各题:
(1)图形1绕点O顺时针旋转90°到图形( )所在的位置。
(2)图形4绕点O( )时针旋转90°到图形3所在的位置。
(3)图形3绕点O逆时针旋转( )度到图形1所在的位置。
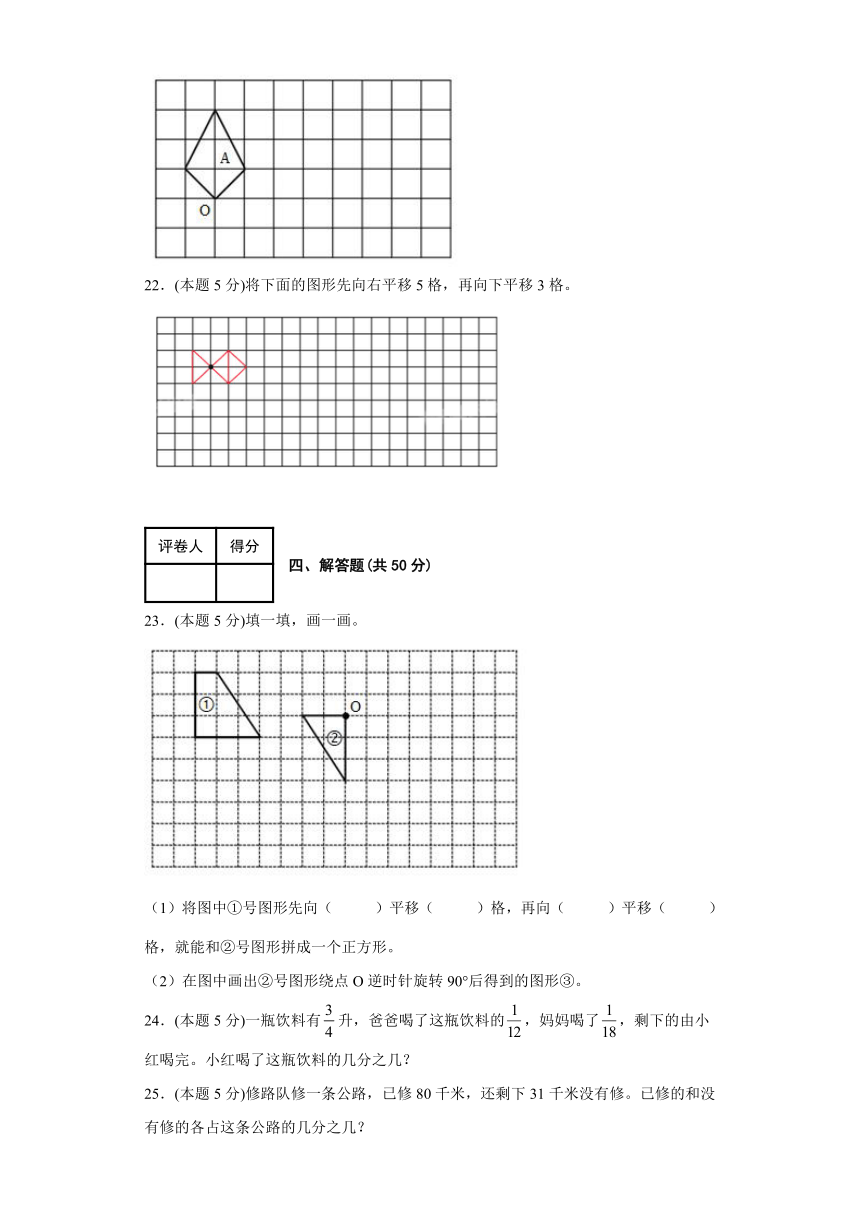
17.(本题2分)看图填空。
(1)铅笔向( )平移( )个方格。
(2)小船向( )平移( )个方格。
(3)笑脸向( )平移( )个方格。
18.(本题2分)看图填空。
(1)图形A向( )平移了( )格,得到图形A/。
(2)图形B向( )平移了( )格,得到图形B/。
(3)图形C向( )平移了( )格,得到图形C/。
19.(本题2分)长方形有( )条对称轴,正方形有( )条对称轴,圆有( )条对称轴。
20.(本题2分)小东5小时行21千米,他平均每小时行( )千米,平均每千米要( )小时。
评卷人得分
三、作图题(共10分)
21.(本题5分)将图绕“O”点按顺时针方向旋转后,得到图形B;再将图形B向右平移5格,得到图形C。在图中画出图形B与图形C。(如图)
22.(本题5分)将下面的图形先向右平移5格,再向下平移3格。
评卷人得分
四、解答题(共50分)
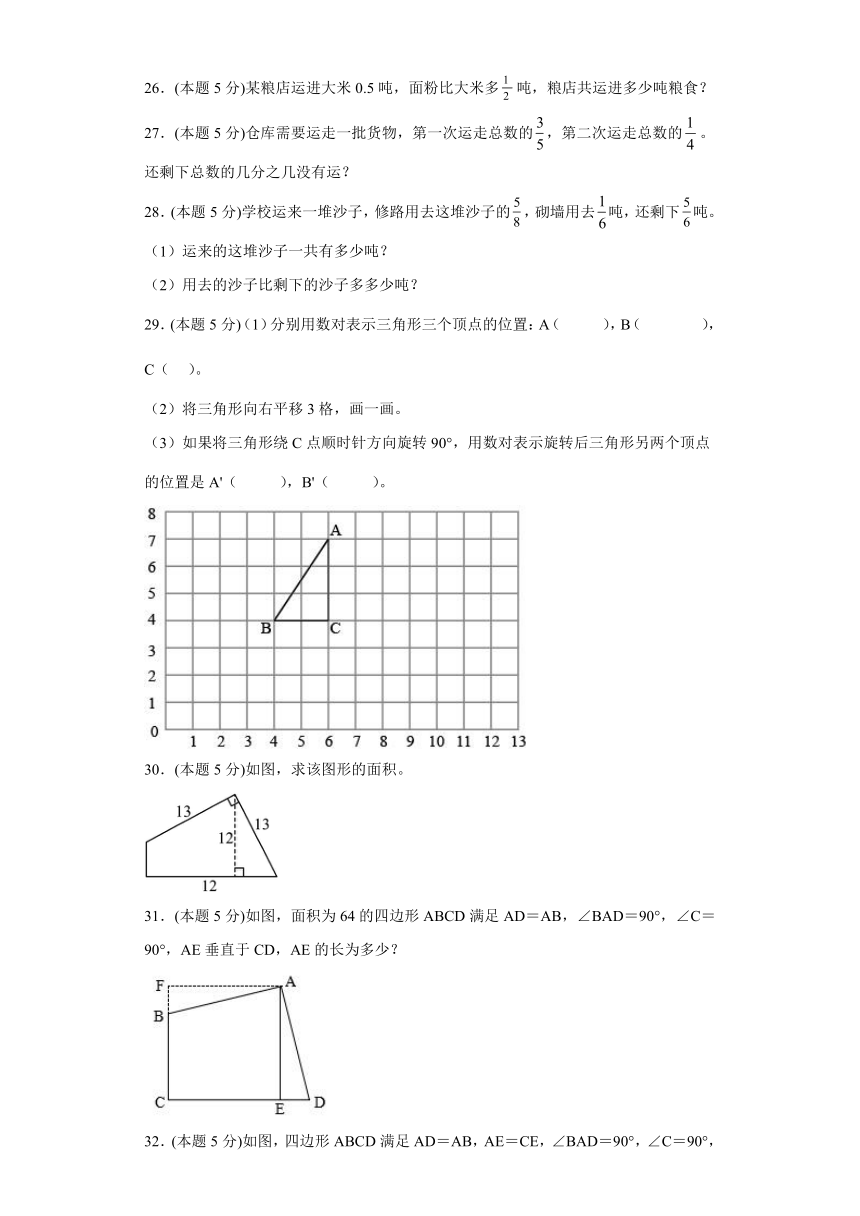
23.(本题5分)填一填,画一画。
(1)将图中①号图形先向( )平移( )格,再向( )平移( )格,就能和②号图形拼成一个正方形。
(2)在图中画出②号图形绕点O逆时针旋转90°后得到的图形③。
24.(本题5分)一瓶饮料有升,爸爸喝了这瓶饮料的,妈妈喝了,剩下的由小红喝完。小红喝了这瓶饮料的几分之几?
25.(本题5分)修路队修一条公路,已修80千米,还剩下31千米没有修。已修的和没有修的各占这条公路的几分之几?
26.(本题5分)某粮店运进大米0.5吨,面粉比大米多吨,粮店共运进多少吨粮食?
27.(本题5分)仓库需要运走一批货物,第一次运走总数的,第二次运走总数的。还剩下总数的几分之几没有运?
28.(本题5分)学校运来一堆沙子,修路用去这堆沙子的,砌墙用去吨,还剩下吨。
(1)运来的这堆沙子一共有多少吨?
(2)用去的沙子比剩下的沙子多多少吨?
29.(本题5分)(1)分别用数对表示三角形三个顶点的位置:A( ),B( ),C( )。
(2)将三角形向右平移3格,画一画。
(3)如果将三角形绕C点顺时针方向旋转90°,用数对表示旋转后三角形另两个顶点的位置是A'( ),B'( )。
30.(本题5分)如图,求该图形的面积。
31.(本题5分)如图,面积为64的四边形ABCD满足AD=AB,∠BAD=90°,∠C=90°,AE垂直于CD,AE的长为多少?
32.(本题5分)如图,四边形ABCD满足AD=AB,AE=CE,∠BAD=90°,∠C=90°,AE垂直CD于E点。如果AE长为4cm,求四边形ABCD的面积。
参考答案:
1.D
【分析】根据对称图形的特点,如果一个图形沿着一条直线对折,两侧图形能够完全重合,这样的图形就是轴对称图形,据此即可解题。
【详解】根据轴对称图形定义可知:把一个圆形纸无论如何对折,两部分都能完全重合,所以圆是轴对称图形,它的对称轴是直径所在直线,而圆有无数条直径,即圆有无数条对称轴。
故答案为:D
【点睛】本题主要考查轴对称图形的对称轴条数,要熟悉轴对称图形的特点,并且根据其特点解决有关问题。
2.C
【分析】按照旋转的要求,确定好物体的旋转中心、旋转方向、旋转角度,按要求进行旋转即可。据此解答。
【详解】A. 涂色部分是由空白部分绕点0顺进针旋转180 得到的。
B. 涂色部分是由空白部分绕点0顺时针旋转的,但旋转的角度不够90°。
C. 涂色部分是由空白部分绕点0顺时针旋转90°得到的。
D. 涂色部分是由空白部分向下翻转得到。
故答案为:C
【点睛】考查了图形的旋转,掌握图形旋转三要素是解答本题的关键。
3.B
【分析】图形旋转前后的形状大小,不会发生变化。据此解题。
【详解】把一个图形绕某个点旋转30°后,所得到的图形与原来的图形相比较,大小不变。
故答案为:B
【点睛】本题考查了旋转,掌握旋转的定义及特征是解题的关键。
4.D
【分析】长方形有两条对称轴,也就是过对边中点的直线;正方形有四条对称轴,即过对边中点的直线和过对角的直线;等边三角形有三条对称轴,即三条高所在的直线;圆形有无数条对称轴,即直径所在的直线。
【详解】A.长方形有两条对称轴;
B. 正方形有四条对称轴;
C. 等边三角形有三条对称轴;
D. 圆形有无数条对称轴;
故答案为:D
【点睛】本题考查轴对称图形的意义,需熟练掌握常见图形的对称轴数量。在所有的平面图形中,圆的对称轴条数最多。
5.B
【分析】旋转中的三要素:旋转点、旋转方向、旋转角度。据此可判断各个选项的正误。
【详解】A.阴影部分绕O点沿顺时针方向旋转,但角度不是90°;
B.阴影部分是由空白部分绕O点顺时针旋转90°得到;
C.阴影部分是由空白部分绕O点顺时针旋转180°得到。
故答案为:B
【点睛】本题主要考查的是图形的旋转,解题的关键是熟练掌握旋转的三要素,进而得出答案。
6.B
【分析】(1)在平面内,把一个图形整体沿某条直线方向平行移动的过程,称为平移。物体或图形平移后,它们的形状、大小、方向都不改变,只是位置发生了变化。
(2)在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角;物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
【详解】根据分析可知,教室门的打开和关闭,门的运动是旋转现象。
故答案为:B
【点睛】正确理解旋转、平移的意义,是解答此题的关键。
7.C
【分析】根据平移和旋转的判断方法:平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动。旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。平移和旋转都是物体的整体运动,所以大小和形状都不会改变。
【详解】根据平移和旋转运动特点,二者都是整体运动,所以平移和旋转都不改变图形的形状和大小。
故答案为:C
【点睛】本题主要考查平移和旋转运动的特点,牢记平移和旋转都不改变图形的形状和大小。
8.B
【分析】将2转化成分母为3的分数,看这个分数里面有多少个,就要连续减多少次,据此解答即可。
【详解】2=,里面有6个,所以需要连续减6次,结果是0;
故答案为:B。
【点睛】熟练掌握整数与分数的互化是解答本题的关键。
9.B
【分析】减法的性质:一个数连续减去两个数,可以用这个数减去两个数的和,即a-b-c=a-(b+c);据此即可得出答案。
【详解】--
=-(+)
=-
=
应用了减法性质。
故答案为:B。
【点睛】这是一道加减法巧算的实际运用题目,根据减法的运算性质来解答。
10.A
【分析】在钟面上,分针每分钟走360°÷60=6°,时针走360°÷(60×12) =0.5°。由于过6分钟后分针和此时刻3分钟前的时针正好方向相反且在一条直线上,此时针与分针的夹角为180°-6°×6-0.5°×3=142.5°。10时整时,时针与分针相差60°。时针与分针每分钟夹角相差6°-0.5°=5.5°,根据追及问题,用(142.5°-60°)除以5.5°就是10时后经过的分钟数,再加10时就是此题的时刻。
【详解】360°÷60=6°
360°÷(60×12)
=360°÷720
=0.5°
180°-6°×6-0.5°×3
=180°-36°-1.5°
=142.5°
6°-0.5°=5.5°
(142.5°-60°)÷5.5°
=82.5°÷5.5°
=15(分)
所以此时是10时15分。
故答案为:A
【点睛】本题考查时间与钟面的应用,解题的关键是:分针每分针走的度数、时针每分钟走的度数、时针与分针在方向相反一条直线上,相差180°。
11. 2 3 4 90°
【分析】在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。旋转的三要素:旋转中心,旋转方向和旋转角度。
【详解】如图,图形1绕点O顺时针旋转90°到图形2所在的位置,图形4绕点O逆时针旋转90°到图形3所在的位置,图形2绕点O顺时针旋转180°到图形4所在的位置,图形2绕点O顺时针旋转90°到图形3所在的位置。
【点睛】此题考查了图形的旋转,关键是熟练掌握图形旋转三要素。
12.
【分析】把单位“1”平均分成若干份,取一份的数叫做分数单位,据此可知的分数单位是,它里面有8个,再减5个这样的单位,还剩3个这样的单位,为,即。
【详解】的分数单位是;
它减去5个这样的单位,结果是。
【点睛】明确分数单位的意义是解答本题的关键。
13. 顺 90
【分析】从12:00至12:15经过了15分钟,分针沿顺时针方向从12转动到3,共转了3大格,旋转角度是:30°×3=90°,据此解答。
【详解】30°×3=90°
从12:00到12:15,分针按顺时针方向旋转了90°。
【点睛】旋转三要素:旋转中心、旋转方向(顺时针或逆时针)、旋转角度,注意,钟面上每一大格所对应的角度是30°。
14. 360 30
【分析】钟面上12个数字,以表芯为旋转点,表针转一圈是360度,被12个数字平均分成12份,360÷12=30,即每一份也就是两个数字之间的夹角30度;从3点到4点,钟上的分针转了一圈,即360度;时针转了一大格,即30度,据此解答。
【详解】根据分析可知,从3点到4点,钟上的分针转了360度,时针转了30度。
【点睛】根据钟面上的角解答问题,关键牢记每一个大格是30度。
15. 240 30
【分析】由于钟面上一大格是30°,根据旋转的定义,找准旋转的方向和旋转的角度即可求解。
【详解】(1)指针从“12”绕点O顺时针旋转到 “8”,走了8个大格,一大格是30°。
30×8=240°
(2)指针从“8”绕点O顺时针旋转到“9”,走了1个大格,是30°。
【点睛】本题考查了生活中的旋转现象,要看清是顺时针还是逆时针旋转,旋转多少度,读懂题意是解答的基础。
16.(1)2
(2)逆
(3)180
【分析】在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。注意旋转的三要素:旋转中心,旋转方向和旋转角度。
(1)
图形1绕点O顺时针旋转90°到图形2所在的位置。
(2)
图形4绕点O逆时针旋转90°到图形3所在的位置。
(3)
图形3绕点O逆时针旋转180度到图形1所在的位置。
【点睛】此题考查了图形的旋转,关键是熟练掌握图形旋转三要素。
17.(1) 下 5
(2) 右 7
(3) 上 4
【分析】物体平移的方法是点对点平移,然后将所有点依次连接起来,依此确定出平移的方向和方格数即可。
(1)
铅笔向下平移5个方格。
(2)
小船向右平移7个方格。
(3)
笑脸向上平移4个方格。
【点睛】熟练掌握物体平移的方法是解答此题的关键。
18.(1) 下 6
(2) 左 5
(3) 上 5
【分析】物体平移的方法是点对点平移,然后将所有点依次连接起来,依此确定出平移的方向和距离即可。
(1)
图形A向下平移了6格,得到图形A/。
(2)
图形B向左平移了5格,得到图形B/。
(3)
图形C向上平移了5格,得到图形C/。
【点睛】熟练掌握物体平移的方法是解答此题的关键。
19. 2 4 无数
【分析】将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,根据对称轴定义找出各图形对称轴的数量。
【详解】长方形的对称轴:每组对边中点连线所在的直线,共有2条对称轴;
正方形的对称轴:每组对边中点连线所在的直线,对角线所在的直线,共有4条对称轴;
圆形的对称轴:将一张圆形纸片对折,折线两侧的部分可以完全重合,圆有无数条对称轴。
由上可知,长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。
【点睛】本题主要考查轴对称图形的认识,掌握对称轴的意义是解答题目的关键。
20. 4.2
【分析】速度=路程÷时间,据此解答即可。
【详解】21÷5=4.2(千米)
5÷21=(小时)
【点睛】本题考查分数与除法的关系、行程问题,解答本题的关键是掌握分数与除法的关系。
21.见详解
【分析】根据旋转的特征,图形A绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后图形B;根据平移的特征,把图形B的各部分分别向右平移5格,即可得到平移后的图形C。
【详解】作图如下:
【点睛】图形平移注意三要素:即原位置、平移方向、平移距离;图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。
22.见详解
【分析】物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画图即可。
【详解】
【点睛】此题考查的是作平移后的图形,熟练掌握平移的特点是解答此题的关键。
23.(1)下;2;右;4
(2)见详解
【分析】(1)可以通过能和②号图形拼成一个正方形时①号图形所在的位置,再与原位置对比,即可确定平移的方向及位置;
(2)根据旋转的特征,把②号图形绕点O按逆时针方向旋转,点O保持不变,其余各部分分别绕O点按逆时针方向旋转相同的度数即可。
【详解】(1)将图中①号图形先向下平移2格,再向右平移4格,就能和②号图形拼成一个正方形。
(2)作图如下:
【点睛】解答本题的关键是要理解和掌握平移及旋转的意义,并能利用旋转的特征进行作图。
24.
【分析】根据题意,可知这瓶饮料的总量为单位“1”,分别减去爸爸和妈妈喝的占这瓶饮料的分率即可。
【详解】1--
=-
=
答:小红喝了这瓶饮料的。
【点睛】解答本题的关键是明确和表示的意义,所以要用单位“1”去减,与没有关系。
25.;
【分析】用80+31求出公路的总长度,再分别用已修的和没有修的长度除以总长度即可。
【详解】80÷(80+31)
=80÷111
=;
31÷(80+31)
=31÷111
=;
答:已修的长度占这条公路的,没有修的长度占这条公路的。
【点睛】求一个数占另一个数的几分之几,用这个数除以另一个数即可。
26.1.5吨
【分析】用大米的质量加上吨即可求出面粉的质量,再与大米的质量相加即可。
【详解】0.5++0.5
=1+0.5
=1.5(吨);
答:粮店共运进1.5吨粮食。
【点睛】掌握分数与小数加减法的计算方法是关键,可以将小数转化成分数计算,也可以将分数转化成小数计算。
27.
【分析】根据题意,可知货物总量为单位“1”,分别减去第一次和第二次运走的占总量的分率即可。
【详解】1--
=-
=;
答:还剩下总数的没有运。
【点睛】本题较易,熟练掌握分数减法的计算方法是解答本题的关键。
28.(1)吨
(2)1吨
【分析】(1)将沙子总吨数看作单位“1”,砌墙用去的吨数和剩下的吨数÷对应分率=总吨数。
(2)总吨数-剩下的吨数=用去的吨数,用去的吨数-剩下的吨数即可。
【详解】(1)(+)÷(1-)
=1÷
=(吨)
答:运来的这堆沙子一共有吨。
(2)-=(吨)
-=1(吨)
答:用去的沙子比剩下的沙子多1吨。
【点睛】关键是确定单位“1”,理解分数除法的意义。
29.(1)A(6,7),B(4,4),C(6,4);
(2)见详解;
(3)图见详解;(9,4),(6,6)。
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,即可分别用数对表示出三角形ABC各顶点的位置。
(2)根据平移图形的特征,把三角形ABC三个顶点分别向右平移3格,再首尾连结各点即可。
(3)根据旋转图形的特征,三角形ABC绕C点顺时针旋转90°后,C点的位置不动,其余各点均绕C点按相同的方向旋转相同的度数,再根据A′B′的位置即可用数对表示出来。
【详解】(1)如图,三角形三个顶点的位置分别是A(6,7),B(4,4),C(6,4)。
(2)将三角形向右平移3格如下图:
(3)将三角形绕C点顺时针方向旋转90°,如下图:
A′(9,4),B′(6,6)。
【点睛】本题考查了平移和旋转,明确平移和旋转的含义及作图方法是解题的关键。
30.144
【分析】
如图,将原三角形绕着点O顺时针旋转90°,原图形可以转化为一个正方形,正方形的边长是12,边长乘边长即可求出图形的面积。
【详解】12×12=144
答:该图形的面积是144。
【点睛】此题考查了图形的旋转,关键要把不规则图形转化为规则图形。
31.8
【分析】观测图形可知,三角形AED以A为旋转中心,通过顺时针旋转90度,旋转到三角形ABF,因为AD=AB,∠C=90°,∠AEC=90°,由此可知四边形AFCE是一个正方形,则四边形ABCD的面积=四边形AFCE=64;根据正方形面积公式:面积=边长×边长,由此求出AE的长。
【详解】旋转三角形AED使四边形ABCD转化成一个四边形AFCE
∠C=90°,∠AEC=90°
AF=AE
四边形AFCE为正方形
四边形ABCD的面积=正方形AFCE=64
8×8=64
AE=8
答:AE的长为8。
【点睛】解答本题的关键是根据旋转的特征,利用旋转把四边形转化为正方形,再根据正方形的面积公式,进行解答。
32.16cm2
【分析】
如图,因为AD=AB,∠BAD=90°,所以将三角形AED绕着点A顺时针旋转90°,四边形ABCD可以转化为一个正方形,正方形的边长为4cm,边长乘边长求出正方形的面积,即为四边形ABCD的面积。
【详解】4×4=16(cm2)
答:四边形ABCD的面积是16cm2。
【点睛】此题考查了图形的旋转,关键要把不规则图形转化为规则图形进行计算。
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、选择题(共20分)
1.(本题2分)圆的对称轴有( )。
A.没有 B.1条 C.2条 D.无数条
2.(本题2分)如图中涂色部分是由空白部分绕点0顺时针旋转90°得到的是( )。
A. B. C. D.
3.(本题2分)把一个图形绕某个点旋转30°后,所得到的图形与原来的图形相比较,( )。
A.变大了 B.大小不变 C.变小了 D.无法确定大小是否变化
4.(本题2分)下列图形中,对称轴条数最多的是( )。
A.长方形 B.正方形 C.等边三角形 D.圆形
5.(本题2分)下图中阴影部分是由空白部分绕点O顺时针旋转90°后得到的是( )。
A. B. C.
6.(本题2分)教室门的打开和关闭,门的运动是( )现象。
A.平移 B.旋转 C.平移和旋转
7.(本题2分)下面说法正确的是( )。
A.旋转改变图形的形状和大小 B.平移改变图形的形状和大小
C.平移和旋转都不改变图形的形状和大小 D.A和B都对
8.(本题2分)从2里面每次减去,需要连续减( )次,结果是0。
A.2 B.6 C.9
9.(本题2分)--=-(+)应用了( )。
A.减法结合律 B.减法性质 C.加法结合律
10.(本题2分)某时刻钟表时针在10点到11点之间,此时刻再过6分钟后分针和此时刻3分钟前的时针正好方向相反且在一条直线上,则此时刻为( )。
A.10点15分 B.10点19分 C.10点20分 D.10点25分
评卷人得分
二、填空题(共20分)
11.(本题2分)如图,图形1绕点O顺时针旋转90°到图形( )所在的位置,图形4绕点O逆时针旋转90°到图形( )所在的位置,图形2绕点O顺时针旋转180°到图形( )所在的位置,图形2绕点O顺时针旋转( )到图形3所在的位置。
12.(本题2分)的分数单位是( ),它减去5个这样的单位,结果是( )。
13.(本题2分)从12:00到12:15,分针按( )时针方向旋转了( ) °。
14.(本题2分)从3点到4点,钟上的分针转了( )度,时针转了( )度。
15.(本题2分)指针从“12”绕点O顺时针旋转( ) °到“8”,再继续顺时针旋转( ) °到“9”。
16.(本题2分)回答下列各题:
(1)图形1绕点O顺时针旋转90°到图形( )所在的位置。
(2)图形4绕点O( )时针旋转90°到图形3所在的位置。
(3)图形3绕点O逆时针旋转( )度到图形1所在的位置。
17.(本题2分)看图填空。
(1)铅笔向( )平移( )个方格。
(2)小船向( )平移( )个方格。
(3)笑脸向( )平移( )个方格。
18.(本题2分)看图填空。
(1)图形A向( )平移了( )格,得到图形A/。
(2)图形B向( )平移了( )格,得到图形B/。
(3)图形C向( )平移了( )格,得到图形C/。
19.(本题2分)长方形有( )条对称轴,正方形有( )条对称轴,圆有( )条对称轴。
20.(本题2分)小东5小时行21千米,他平均每小时行( )千米,平均每千米要( )小时。
评卷人得分
三、作图题(共10分)
21.(本题5分)将图绕“O”点按顺时针方向旋转后,得到图形B;再将图形B向右平移5格,得到图形C。在图中画出图形B与图形C。(如图)
22.(本题5分)将下面的图形先向右平移5格,再向下平移3格。
评卷人得分
四、解答题(共50分)
23.(本题5分)填一填,画一画。
(1)将图中①号图形先向( )平移( )格,再向( )平移( )格,就能和②号图形拼成一个正方形。
(2)在图中画出②号图形绕点O逆时针旋转90°后得到的图形③。
24.(本题5分)一瓶饮料有升,爸爸喝了这瓶饮料的,妈妈喝了,剩下的由小红喝完。小红喝了这瓶饮料的几分之几?
25.(本题5分)修路队修一条公路,已修80千米,还剩下31千米没有修。已修的和没有修的各占这条公路的几分之几?
26.(本题5分)某粮店运进大米0.5吨,面粉比大米多吨,粮店共运进多少吨粮食?
27.(本题5分)仓库需要运走一批货物,第一次运走总数的,第二次运走总数的。还剩下总数的几分之几没有运?
28.(本题5分)学校运来一堆沙子,修路用去这堆沙子的,砌墙用去吨,还剩下吨。
(1)运来的这堆沙子一共有多少吨?
(2)用去的沙子比剩下的沙子多多少吨?
29.(本题5分)(1)分别用数对表示三角形三个顶点的位置:A( ),B( ),C( )。
(2)将三角形向右平移3格,画一画。
(3)如果将三角形绕C点顺时针方向旋转90°,用数对表示旋转后三角形另两个顶点的位置是A'( ),B'( )。
30.(本题5分)如图,求该图形的面积。
31.(本题5分)如图,面积为64的四边形ABCD满足AD=AB,∠BAD=90°,∠C=90°,AE垂直于CD,AE的长为多少?
32.(本题5分)如图,四边形ABCD满足AD=AB,AE=CE,∠BAD=90°,∠C=90°,AE垂直CD于E点。如果AE长为4cm,求四边形ABCD的面积。
参考答案:
1.D
【分析】根据对称图形的特点,如果一个图形沿着一条直线对折,两侧图形能够完全重合,这样的图形就是轴对称图形,据此即可解题。
【详解】根据轴对称图形定义可知:把一个圆形纸无论如何对折,两部分都能完全重合,所以圆是轴对称图形,它的对称轴是直径所在直线,而圆有无数条直径,即圆有无数条对称轴。
故答案为:D
【点睛】本题主要考查轴对称图形的对称轴条数,要熟悉轴对称图形的特点,并且根据其特点解决有关问题。
2.C
【分析】按照旋转的要求,确定好物体的旋转中心、旋转方向、旋转角度,按要求进行旋转即可。据此解答。
【详解】A. 涂色部分是由空白部分绕点0顺进针旋转180 得到的。
B. 涂色部分是由空白部分绕点0顺时针旋转的,但旋转的角度不够90°。
C. 涂色部分是由空白部分绕点0顺时针旋转90°得到的。
D. 涂色部分是由空白部分向下翻转得到。
故答案为:C
【点睛】考查了图形的旋转,掌握图形旋转三要素是解答本题的关键。
3.B
【分析】图形旋转前后的形状大小,不会发生变化。据此解题。
【详解】把一个图形绕某个点旋转30°后,所得到的图形与原来的图形相比较,大小不变。
故答案为:B
【点睛】本题考查了旋转,掌握旋转的定义及特征是解题的关键。
4.D
【分析】长方形有两条对称轴,也就是过对边中点的直线;正方形有四条对称轴,即过对边中点的直线和过对角的直线;等边三角形有三条对称轴,即三条高所在的直线;圆形有无数条对称轴,即直径所在的直线。
【详解】A.长方形有两条对称轴;
B. 正方形有四条对称轴;
C. 等边三角形有三条对称轴;
D. 圆形有无数条对称轴;
故答案为:D
【点睛】本题考查轴对称图形的意义,需熟练掌握常见图形的对称轴数量。在所有的平面图形中,圆的对称轴条数最多。
5.B
【分析】旋转中的三要素:旋转点、旋转方向、旋转角度。据此可判断各个选项的正误。
【详解】A.阴影部分绕O点沿顺时针方向旋转,但角度不是90°;
B.阴影部分是由空白部分绕O点顺时针旋转90°得到;
C.阴影部分是由空白部分绕O点顺时针旋转180°得到。
故答案为:B
【点睛】本题主要考查的是图形的旋转,解题的关键是熟练掌握旋转的三要素,进而得出答案。
6.B
【分析】(1)在平面内,把一个图形整体沿某条直线方向平行移动的过程,称为平移。物体或图形平移后,它们的形状、大小、方向都不改变,只是位置发生了变化。
(2)在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角;物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
【详解】根据分析可知,教室门的打开和关闭,门的运动是旋转现象。
故答案为:B
【点睛】正确理解旋转、平移的意义,是解答此题的关键。
7.C
【分析】根据平移和旋转的判断方法:平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动。旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。平移和旋转都是物体的整体运动,所以大小和形状都不会改变。
【详解】根据平移和旋转运动特点,二者都是整体运动,所以平移和旋转都不改变图形的形状和大小。
故答案为:C
【点睛】本题主要考查平移和旋转运动的特点,牢记平移和旋转都不改变图形的形状和大小。
8.B
【分析】将2转化成分母为3的分数,看这个分数里面有多少个,就要连续减多少次,据此解答即可。
【详解】2=,里面有6个,所以需要连续减6次,结果是0;
故答案为:B。
【点睛】熟练掌握整数与分数的互化是解答本题的关键。
9.B
【分析】减法的性质:一个数连续减去两个数,可以用这个数减去两个数的和,即a-b-c=a-(b+c);据此即可得出答案。
【详解】--
=-(+)
=-
=
应用了减法性质。
故答案为:B。
【点睛】这是一道加减法巧算的实际运用题目,根据减法的运算性质来解答。
10.A
【分析】在钟面上,分针每分钟走360°÷60=6°,时针走360°÷(60×12) =0.5°。由于过6分钟后分针和此时刻3分钟前的时针正好方向相反且在一条直线上,此时针与分针的夹角为180°-6°×6-0.5°×3=142.5°。10时整时,时针与分针相差60°。时针与分针每分钟夹角相差6°-0.5°=5.5°,根据追及问题,用(142.5°-60°)除以5.5°就是10时后经过的分钟数,再加10时就是此题的时刻。
【详解】360°÷60=6°
360°÷(60×12)
=360°÷720
=0.5°
180°-6°×6-0.5°×3
=180°-36°-1.5°
=142.5°
6°-0.5°=5.5°
(142.5°-60°)÷5.5°
=82.5°÷5.5°
=15(分)
所以此时是10时15分。
故答案为:A
【点睛】本题考查时间与钟面的应用,解题的关键是:分针每分针走的度数、时针每分钟走的度数、时针与分针在方向相反一条直线上,相差180°。
11. 2 3 4 90°
【分析】在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。旋转的三要素:旋转中心,旋转方向和旋转角度。
【详解】如图,图形1绕点O顺时针旋转90°到图形2所在的位置,图形4绕点O逆时针旋转90°到图形3所在的位置,图形2绕点O顺时针旋转180°到图形4所在的位置,图形2绕点O顺时针旋转90°到图形3所在的位置。
【点睛】此题考查了图形的旋转,关键是熟练掌握图形旋转三要素。
12.
【分析】把单位“1”平均分成若干份,取一份的数叫做分数单位,据此可知的分数单位是,它里面有8个,再减5个这样的单位,还剩3个这样的单位,为,即。
【详解】的分数单位是;
它减去5个这样的单位,结果是。
【点睛】明确分数单位的意义是解答本题的关键。
13. 顺 90
【分析】从12:00至12:15经过了15分钟,分针沿顺时针方向从12转动到3,共转了3大格,旋转角度是:30°×3=90°,据此解答。
【详解】30°×3=90°
从12:00到12:15,分针按顺时针方向旋转了90°。
【点睛】旋转三要素:旋转中心、旋转方向(顺时针或逆时针)、旋转角度,注意,钟面上每一大格所对应的角度是30°。
14. 360 30
【分析】钟面上12个数字,以表芯为旋转点,表针转一圈是360度,被12个数字平均分成12份,360÷12=30,即每一份也就是两个数字之间的夹角30度;从3点到4点,钟上的分针转了一圈,即360度;时针转了一大格,即30度,据此解答。
【详解】根据分析可知,从3点到4点,钟上的分针转了360度,时针转了30度。
【点睛】根据钟面上的角解答问题,关键牢记每一个大格是30度。
15. 240 30
【分析】由于钟面上一大格是30°,根据旋转的定义,找准旋转的方向和旋转的角度即可求解。
【详解】(1)指针从“12”绕点O顺时针旋转到 “8”,走了8个大格,一大格是30°。
30×8=240°
(2)指针从“8”绕点O顺时针旋转到“9”,走了1个大格,是30°。
【点睛】本题考查了生活中的旋转现象,要看清是顺时针还是逆时针旋转,旋转多少度,读懂题意是解答的基础。
16.(1)2
(2)逆
(3)180
【分析】在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。注意旋转的三要素:旋转中心,旋转方向和旋转角度。
(1)
图形1绕点O顺时针旋转90°到图形2所在的位置。
(2)
图形4绕点O逆时针旋转90°到图形3所在的位置。
(3)
图形3绕点O逆时针旋转180度到图形1所在的位置。
【点睛】此题考查了图形的旋转,关键是熟练掌握图形旋转三要素。
17.(1) 下 5
(2) 右 7
(3) 上 4
【分析】物体平移的方法是点对点平移,然后将所有点依次连接起来,依此确定出平移的方向和方格数即可。
(1)
铅笔向下平移5个方格。
(2)
小船向右平移7个方格。
(3)
笑脸向上平移4个方格。
【点睛】熟练掌握物体平移的方法是解答此题的关键。
18.(1) 下 6
(2) 左 5
(3) 上 5
【分析】物体平移的方法是点对点平移,然后将所有点依次连接起来,依此确定出平移的方向和距离即可。
(1)
图形A向下平移了6格,得到图形A/。
(2)
图形B向左平移了5格,得到图形B/。
(3)
图形C向上平移了5格,得到图形C/。
【点睛】熟练掌握物体平移的方法是解答此题的关键。
19. 2 4 无数
【分析】将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,根据对称轴定义找出各图形对称轴的数量。
【详解】长方形的对称轴:每组对边中点连线所在的直线,共有2条对称轴;
正方形的对称轴:每组对边中点连线所在的直线,对角线所在的直线,共有4条对称轴;
圆形的对称轴:将一张圆形纸片对折,折线两侧的部分可以完全重合,圆有无数条对称轴。
由上可知,长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。
【点睛】本题主要考查轴对称图形的认识,掌握对称轴的意义是解答题目的关键。
20. 4.2
【分析】速度=路程÷时间,据此解答即可。
【详解】21÷5=4.2(千米)
5÷21=(小时)
【点睛】本题考查分数与除法的关系、行程问题,解答本题的关键是掌握分数与除法的关系。
21.见详解
【分析】根据旋转的特征,图形A绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后图形B;根据平移的特征,把图形B的各部分分别向右平移5格,即可得到平移后的图形C。
【详解】作图如下:
【点睛】图形平移注意三要素:即原位置、平移方向、平移距离;图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。
22.见详解
【分析】物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画图即可。
【详解】
【点睛】此题考查的是作平移后的图形,熟练掌握平移的特点是解答此题的关键。
23.(1)下;2;右;4
(2)见详解
【分析】(1)可以通过能和②号图形拼成一个正方形时①号图形所在的位置,再与原位置对比,即可确定平移的方向及位置;
(2)根据旋转的特征,把②号图形绕点O按逆时针方向旋转,点O保持不变,其余各部分分别绕O点按逆时针方向旋转相同的度数即可。
【详解】(1)将图中①号图形先向下平移2格,再向右平移4格,就能和②号图形拼成一个正方形。
(2)作图如下:
【点睛】解答本题的关键是要理解和掌握平移及旋转的意义,并能利用旋转的特征进行作图。
24.
【分析】根据题意,可知这瓶饮料的总量为单位“1”,分别减去爸爸和妈妈喝的占这瓶饮料的分率即可。
【详解】1--
=-
=
答:小红喝了这瓶饮料的。
【点睛】解答本题的关键是明确和表示的意义,所以要用单位“1”去减,与没有关系。
25.;
【分析】用80+31求出公路的总长度,再分别用已修的和没有修的长度除以总长度即可。
【详解】80÷(80+31)
=80÷111
=;
31÷(80+31)
=31÷111
=;
答:已修的长度占这条公路的,没有修的长度占这条公路的。
【点睛】求一个数占另一个数的几分之几,用这个数除以另一个数即可。
26.1.5吨
【分析】用大米的质量加上吨即可求出面粉的质量,再与大米的质量相加即可。
【详解】0.5++0.5
=1+0.5
=1.5(吨);
答:粮店共运进1.5吨粮食。
【点睛】掌握分数与小数加减法的计算方法是关键,可以将小数转化成分数计算,也可以将分数转化成小数计算。
27.
【分析】根据题意,可知货物总量为单位“1”,分别减去第一次和第二次运走的占总量的分率即可。
【详解】1--
=-
=;
答:还剩下总数的没有运。
【点睛】本题较易,熟练掌握分数减法的计算方法是解答本题的关键。
28.(1)吨
(2)1吨
【分析】(1)将沙子总吨数看作单位“1”,砌墙用去的吨数和剩下的吨数÷对应分率=总吨数。
(2)总吨数-剩下的吨数=用去的吨数,用去的吨数-剩下的吨数即可。
【详解】(1)(+)÷(1-)
=1÷
=(吨)
答:运来的这堆沙子一共有吨。
(2)-=(吨)
-=1(吨)
答:用去的沙子比剩下的沙子多1吨。
【点睛】关键是确定单位“1”,理解分数除法的意义。
29.(1)A(6,7),B(4,4),C(6,4);
(2)见详解;
(3)图见详解;(9,4),(6,6)。
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,即可分别用数对表示出三角形ABC各顶点的位置。
(2)根据平移图形的特征,把三角形ABC三个顶点分别向右平移3格,再首尾连结各点即可。
(3)根据旋转图形的特征,三角形ABC绕C点顺时针旋转90°后,C点的位置不动,其余各点均绕C点按相同的方向旋转相同的度数,再根据A′B′的位置即可用数对表示出来。
【详解】(1)如图,三角形三个顶点的位置分别是A(6,7),B(4,4),C(6,4)。
(2)将三角形向右平移3格如下图:
(3)将三角形绕C点顺时针方向旋转90°,如下图:
A′(9,4),B′(6,6)。
【点睛】本题考查了平移和旋转,明确平移和旋转的含义及作图方法是解题的关键。
30.144
【分析】
如图,将原三角形绕着点O顺时针旋转90°,原图形可以转化为一个正方形,正方形的边长是12,边长乘边长即可求出图形的面积。
【详解】12×12=144
答:该图形的面积是144。
【点睛】此题考查了图形的旋转,关键要把不规则图形转化为规则图形。
31.8
【分析】观测图形可知,三角形AED以A为旋转中心,通过顺时针旋转90度,旋转到三角形ABF,因为AD=AB,∠C=90°,∠AEC=90°,由此可知四边形AFCE是一个正方形,则四边形ABCD的面积=四边形AFCE=64;根据正方形面积公式:面积=边长×边长,由此求出AE的长。
【详解】旋转三角形AED使四边形ABCD转化成一个四边形AFCE
∠C=90°,∠AEC=90°
AF=AE
四边形AFCE为正方形
四边形ABCD的面积=正方形AFCE=64
8×8=64
AE=8
答:AE的长为8。
【点睛】解答本题的关键是根据旋转的特征,利用旋转把四边形转化为正方形,再根据正方形的面积公式,进行解答。
32.16cm2
【分析】
如图,因为AD=AB,∠BAD=90°,所以将三角形AED绕着点A顺时针旋转90°,四边形ABCD可以转化为一个正方形,正方形的边长为4cm,边长乘边长求出正方形的面积,即为四边形ABCD的面积。
【详解】4×4=16(cm2)
答:四边形ABCD的面积是16cm2。
【点睛】此题考查了图形的旋转,关键要把不规则图形转化为规则图形进行计算。
