5.3.1函数的单调性 课件(共22张PPT)
文档属性
| 名称 | 5.3.1函数的单调性 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 616.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 23:04:01 | ||
图片预览








文档简介
(共22张PPT)
5.3.1 函数的单调性
第五章
◆ 教学目标
1.通过具体函数图象,发现函数的单调性与导数的正负之间的关系,体会数形结合思想,发展直观想象素养.
2.能根据函数导数的正负判断函数的单调性,体会算法思想,发展数学运算素养.
◆ 教学重难点
教学重点:理解函数的单调性与导数的正负之间的关系.
教学难点:运用导数判断函数的单调性
新课导入
问题1:阅读课本第84~87页,回答下列问题:
(1)本节将要探究哪类问题?
(2)本节探究的起点是什么?目标是什么?
在必修第一册中,我们通过图象直观,利用不等式、方程等知识,研究了函数的单调性、周期性、奇偶性以及最大(小)值等性质.
在本章前两节中,我们学习了导数的概念和运算,知道导数是关于瞬时变化率的数学表达,它定量地刻画了函数的局部变化.
问题2:能否利用导数更加精确地研究函数的性质呢?
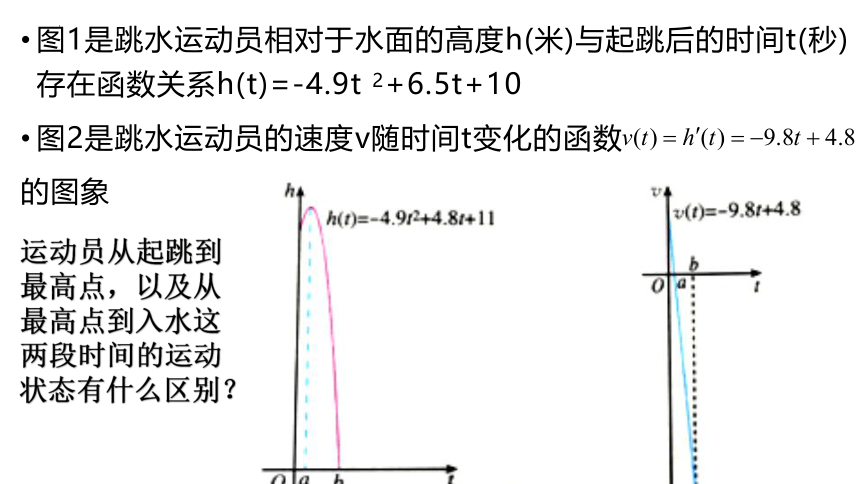
图1是跳水运动员相对于水面的高度h(米)与起跳后的时间t(秒)存在函数关系h(t)=-4.9t 2+6.5t+10
图2是跳水运动员的速度v随时间t变化的函数
的图象
运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
探究新知
知识点1:函数的单调性与导数的符号之间的关系
观察图象可以发现:
1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即h(t)单调递增.相应地.
2)从最高点到入水,运功员的重心处于下降状态,画水面的高度h随时间t的增加而减小,即h(t)单调递减.相应地 .
问题4:从以上观察中发现,函数h(t)的单调性与 的正负有内在联系.那么,我们能否由 的正负来判断函数h(t)的单调性呢?
问题探究
问题5:观察下面函数的图象,探讨函数的单调性与导数的正负的关系.
从函数导数的几何意义理解函数的单调性与导数的正负之间的关系:
导数f (x0)表示函数 f(x)在点(x0, f(x0))处的切线的斜率.
在x=x0, f′(x0)<0
函数的图象是下降的,
函数f(x)在x=x1附近单调递减;
在x=x0, f′(x0)>0
函数的图象是上升的,
函数f(x)在x=x0附近单调递增;
【想一想】
判断正误(正确的打“√”,错误的打“×”)
(1)函数f (x)在区间(a,b)上都有f ′(x)<0,则函数f (x)在这个区间上单调递减. ( )
(2) 判断函数单调性时,在区间内的个别点f ′(x)=0,不影响函数在此区间的单调性.( )
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x;
(2)f(x)=sinx-x;
(3)f(x)=
方法总结:
用解不等式法求单调区间的步骤:
(1)确定函数f(x)的定义域;
(2)求导函数f (x);
(3)解不等式f (x)>0或f ′(x)<0,并写出解集;
(4)根据(3)的结果确定函数f(x)的单调区间.
例2. 已知导函数 f(x) 的下列信息,试画出函数 f(x) 的图象的大致形状.
当1 < x < 4 时, f (x)>0;
当 x > 4 , 或 x < 1时, f (x)<0;
当 x = 4 , 或 x = 1时,f (x)= 0.
方法总结:研究函数图象与其导函数图象之间的关系的着手点:
研究一个函数图象与其导函数图象之间的关系时,注意抓住各自的关键要素.对于原函数,要注意其图象在哪个区间内单调递增、在哪个区间内单调递减;而对于导函数,则应注意其函数值在哪个区间内大于零、在哪个区间内小于零,并分析这些区间与原函数的单调区间是否一致.
练习:
教科书P87 练习1、2
课堂总结
总结概括
函数f (x)的单调性与导函数f ′(x)正负的关系
定义在区间(a,b)内的函数y=f (x):
f ′(x)的正负 f (x)的单调性
f ′(x)>0 单调递增
f ′(x)<0 单调递减
目标检测设计
1.导函数y=f ′(x)的图象如图所示,则函数y=f (x)的图象可能是( )
2.下列函数中,在 上为增函数的是( )
A.y=sinx
B.y=xex
C.y=x3+3x
D.y=lnx-x
3.函数y=lnx-x的单调递减区间为( )
4.已知函数y=x2-5x+2ln(2x),则的单调递增区间为_____________.
5.3.1 函数的单调性
第五章
◆ 教学目标
1.通过具体函数图象,发现函数的单调性与导数的正负之间的关系,体会数形结合思想,发展直观想象素养.
2.能根据函数导数的正负判断函数的单调性,体会算法思想,发展数学运算素养.
◆ 教学重难点
教学重点:理解函数的单调性与导数的正负之间的关系.
教学难点:运用导数判断函数的单调性
新课导入
问题1:阅读课本第84~87页,回答下列问题:
(1)本节将要探究哪类问题?
(2)本节探究的起点是什么?目标是什么?
在必修第一册中,我们通过图象直观,利用不等式、方程等知识,研究了函数的单调性、周期性、奇偶性以及最大(小)值等性质.
在本章前两节中,我们学习了导数的概念和运算,知道导数是关于瞬时变化率的数学表达,它定量地刻画了函数的局部变化.
问题2:能否利用导数更加精确地研究函数的性质呢?
图1是跳水运动员相对于水面的高度h(米)与起跳后的时间t(秒)存在函数关系h(t)=-4.9t 2+6.5t+10
图2是跳水运动员的速度v随时间t变化的函数
的图象
运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
探究新知
知识点1:函数的单调性与导数的符号之间的关系
观察图象可以发现:
1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即h(t)单调递增.相应地.
2)从最高点到入水,运功员的重心处于下降状态,画水面的高度h随时间t的增加而减小,即h(t)单调递减.相应地 .
问题4:从以上观察中发现,函数h(t)的单调性与 的正负有内在联系.那么,我们能否由 的正负来判断函数h(t)的单调性呢?
问题探究
问题5:观察下面函数的图象,探讨函数的单调性与导数的正负的关系.
从函数导数的几何意义理解函数的单调性与导数的正负之间的关系:
导数f (x0)表示函数 f(x)在点(x0, f(x0))处的切线的斜率.
在x=x0, f′(x0)<0
函数的图象是下降的,
函数f(x)在x=x1附近单调递减;
在x=x0, f′(x0)>0
函数的图象是上升的,
函数f(x)在x=x0附近单调递增;
【想一想】
判断正误(正确的打“√”,错误的打“×”)
(1)函数f (x)在区间(a,b)上都有f ′(x)<0,则函数f (x)在这个区间上单调递减. ( )
(2) 判断函数单调性时,在区间内的个别点f ′(x)=0,不影响函数在此区间的单调性.( )
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x;
(2)f(x)=sinx-x;
(3)f(x)=
方法总结:
用解不等式法求单调区间的步骤:
(1)确定函数f(x)的定义域;
(2)求导函数f (x);
(3)解不等式f (x)>0或f ′(x)<0,并写出解集;
(4)根据(3)的结果确定函数f(x)的单调区间.
例2. 已知导函数 f(x) 的下列信息,试画出函数 f(x) 的图象的大致形状.
当1 < x < 4 时, f (x)>0;
当 x > 4 , 或 x < 1时, f (x)<0;
当 x = 4 , 或 x = 1时,f (x)= 0.
方法总结:研究函数图象与其导函数图象之间的关系的着手点:
研究一个函数图象与其导函数图象之间的关系时,注意抓住各自的关键要素.对于原函数,要注意其图象在哪个区间内单调递增、在哪个区间内单调递减;而对于导函数,则应注意其函数值在哪个区间内大于零、在哪个区间内小于零,并分析这些区间与原函数的单调区间是否一致.
练习:
教科书P87 练习1、2
课堂总结
总结概括
函数f (x)的单调性与导函数f ′(x)正负的关系
定义在区间(a,b)内的函数y=f (x):
f ′(x)的正负 f (x)的单调性
f ′(x)>0 单调递增
f ′(x)<0 单调递减
目标检测设计
1.导函数y=f ′(x)的图象如图所示,则函数y=f (x)的图象可能是( )
2.下列函数中,在 上为增函数的是( )
A.y=sinx
B.y=xex
C.y=x3+3x
D.y=lnx-x
3.函数y=lnx-x的单调递减区间为( )
4.已知函数y=x2-5x+2ln(2x),则的单调递增区间为_____________.
