5.4二次函数的图象和性质(1) 课件(共12张PPT)2022-2023学年青岛版九年级数学下册
文档属性
| 名称 | 5.4二次函数的图象和性质(1) 课件(共12张PPT)2022-2023学年青岛版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 356.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-18 11:20:22 | ||
图片预览



文档简介
(共12张PPT)
5.4二次函数的图象和性质
今天与明天
今天再晚也是早
明天再早也是晚
把握今天成就明天
学习目标
一、低阶目标
1.利用描点法画函数y=x ,
y=-x 的图象,并能根据图象认识和理解二次函数的性质.
2.能够运用二次函数的性质求待定字母的值(或取值范围).
二、高阶目标
3.在对二次函数的图象由特殊到一般的探究过程中,感受研究函数的基本方法以及分类和数形结合思想、数学建模思想.
达成评价
1.能根据a的不同取值画出不同的二次函数并认识和理解二次函数的性质
2.能运用二次函数的性质求待定字母的值(或取值范围)
3.对二次函数的图象由特殊到一般的探究过程中,感受研究函数的基本方法以及分类和数形结合思想、数学建模思想.
先行组织
1.画一个函数图象的一般过程是① ;② ;③ .
2.一次函数的解析式为______________,图象的形状是 ,性质有___________________________________________________;
3.反比例函数解析式___________________,图象的形状是_________,性质有_____________________________________;
4.二次函数的一般形式:y=ax2+bx+c(a≠0),当 时,为y=ax2+c的形式;当 时,即为y=ax2的形式.
1.列表
2.描点
3.连线
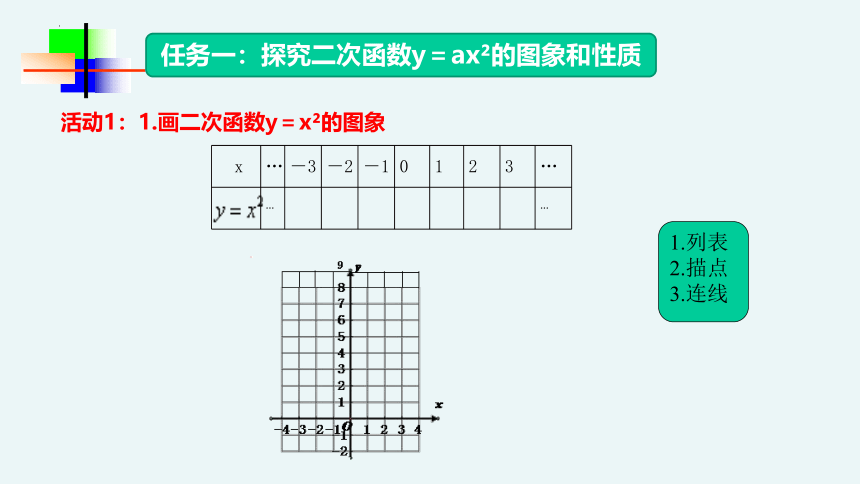
任务一:探究二次函数y=ax 的图象和性质
活动1:1.画二次函数y=x 的图象
x … -3 -2 -1 0 1 2 3 …
… …
归纳:
①由图象可知二次函数y=x 的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,即抛出物体所经过的路线,所以这条曲线叫做 线;
②抛物线y=x 是轴对称图形,对称轴是 ;
③y=x 的图象开口_______;
④ y=x 与 的交点叫做抛物线的顶点;抛物线的顶点坐标是 ;它是抛物线的最____点(填“高”或“低”),即当x=0时,y有最____值等于0;
⑤在对称轴的左侧,图象从左往右呈 趋势,在对称轴的右侧,图象从左往右呈 趋势;即当 时,y随的增大而 ,当 时,y随的增大而 .
1.列表
2.描点
3.连线
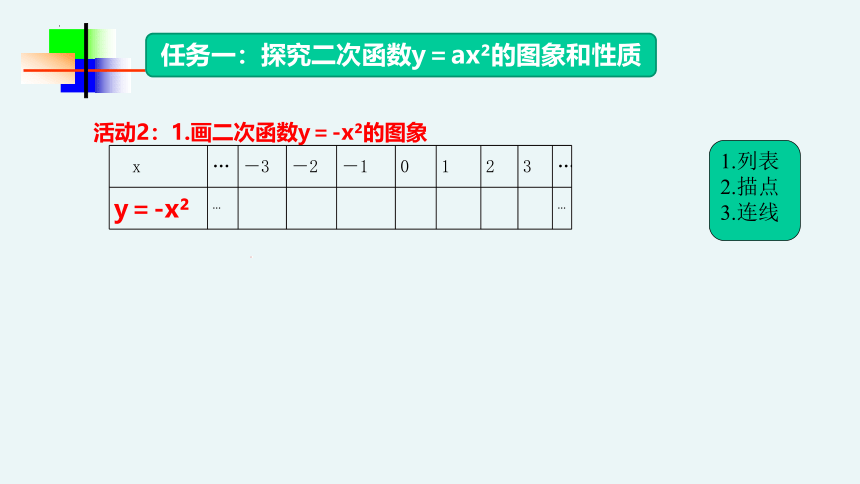
任务一:探究二次函数y=ax 的图象和性质
活动2:1.画二次函数y=-x 的图象
x … -3 -2 -1 0 1 2 3 …
y=-x … …
归纳:
①由图象可知二次函数y=-x 的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,即抛出物体所经过的路线,所以这条曲线叫做 线;
②抛物线y=-x 是轴对称图形,对称轴是 ;
③y=-x 的图象开口_______;
④ y=-x 与 的交点叫做抛物线的顶点;抛物线的顶点坐标是 ;它是抛物线的最____点(填“高”或“低”),即当x=0时,y有最____值等于0;
⑤在对称轴的左侧,图象从左往右呈 趋势,在对称轴的右侧,图象从左往右呈 趋势;即当 时,y随的增大而 ,当 时,y随的增大而 .
任务二:在同一直角坐标系中探究二次函数开口大小与 的关系
图中是y=-2x ,y=-x ,y=- x ,y= x ,y=x ,y=2x 图象.观察有什么共同特征?
在同一直角坐标系中探究二次函数开口大小与 的关系
抛物线的图象性质:
(1)开口方向:当 a>0时,抛物线的开口向_____,顶点是抛物线的最____点,当 a<0时,抛物线的开口向_______,顶点是抛物线的最____点; 越大,抛物线的开口越______;
(2)对称轴:_________;(3)顶点坐标:_________;
(4)增减性:_________ _________________;
(5)函数的最值:当 a<0时,抛物线有最_____点,当x=____时,y有最___值______;当 a>0时,抛物线有最____点,当x=____时,y有最_____值______.
归纳小结:
任务三:应用二次函数的性质求待定系数字母的值(或取值范围)
例:已知函数是关于x的二次函数,求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时x为何值时,y随x的增大而增大;
(3)m为何值时,抛物线有最大值?最大值是多少?当x为何值时,y随x的增大而减小?
成果集成
1.抛物线的图象性质
2.在同一直角坐标系中探究二次函数开口大小与 的关系
下课!
同学们,再见!
5.4二次函数的图象和性质
今天与明天
今天再晚也是早
明天再早也是晚
把握今天成就明天
学习目标
一、低阶目标
1.利用描点法画函数y=x ,
y=-x 的图象,并能根据图象认识和理解二次函数的性质.
2.能够运用二次函数的性质求待定字母的值(或取值范围).
二、高阶目标
3.在对二次函数的图象由特殊到一般的探究过程中,感受研究函数的基本方法以及分类和数形结合思想、数学建模思想.
达成评价
1.能根据a的不同取值画出不同的二次函数并认识和理解二次函数的性质
2.能运用二次函数的性质求待定字母的值(或取值范围)
3.对二次函数的图象由特殊到一般的探究过程中,感受研究函数的基本方法以及分类和数形结合思想、数学建模思想.
先行组织
1.画一个函数图象的一般过程是① ;② ;③ .
2.一次函数的解析式为______________,图象的形状是 ,性质有___________________________________________________;
3.反比例函数解析式___________________,图象的形状是_________,性质有_____________________________________;
4.二次函数的一般形式:y=ax2+bx+c(a≠0),当 时,为y=ax2+c的形式;当 时,即为y=ax2的形式.
1.列表
2.描点
3.连线
任务一:探究二次函数y=ax 的图象和性质
活动1:1.画二次函数y=x 的图象
x … -3 -2 -1 0 1 2 3 …
… …
归纳:
①由图象可知二次函数y=x 的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,即抛出物体所经过的路线,所以这条曲线叫做 线;
②抛物线y=x 是轴对称图形,对称轴是 ;
③y=x 的图象开口_______;
④ y=x 与 的交点叫做抛物线的顶点;抛物线的顶点坐标是 ;它是抛物线的最____点(填“高”或“低”),即当x=0时,y有最____值等于0;
⑤在对称轴的左侧,图象从左往右呈 趋势,在对称轴的右侧,图象从左往右呈 趋势;即当 时,y随的增大而 ,当 时,y随的增大而 .
1.列表
2.描点
3.连线
任务一:探究二次函数y=ax 的图象和性质
活动2:1.画二次函数y=-x 的图象
x … -3 -2 -1 0 1 2 3 …
y=-x … …
归纳:
①由图象可知二次函数y=-x 的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,即抛出物体所经过的路线,所以这条曲线叫做 线;
②抛物线y=-x 是轴对称图形,对称轴是 ;
③y=-x 的图象开口_______;
④ y=-x 与 的交点叫做抛物线的顶点;抛物线的顶点坐标是 ;它是抛物线的最____点(填“高”或“低”),即当x=0时,y有最____值等于0;
⑤在对称轴的左侧,图象从左往右呈 趋势,在对称轴的右侧,图象从左往右呈 趋势;即当 时,y随的增大而 ,当 时,y随的增大而 .
任务二:在同一直角坐标系中探究二次函数开口大小与 的关系
图中是y=-2x ,y=-x ,y=- x ,y= x ,y=x ,y=2x 图象.观察有什么共同特征?
在同一直角坐标系中探究二次函数开口大小与 的关系
抛物线的图象性质:
(1)开口方向:当 a>0时,抛物线的开口向_____,顶点是抛物线的最____点,当 a<0时,抛物线的开口向_______,顶点是抛物线的最____点; 越大,抛物线的开口越______;
(2)对称轴:_________;(3)顶点坐标:_________;
(4)增减性:_________ _________________;
(5)函数的最值:当 a<0时,抛物线有最_____点,当x=____时,y有最___值______;当 a>0时,抛物线有最____点,当x=____时,y有最_____值______.
归纳小结:
任务三:应用二次函数的性质求待定系数字母的值(或取值范围)
例:已知函数是关于x的二次函数,求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时x为何值时,y随x的增大而增大;
(3)m为何值时,抛物线有最大值?最大值是多少?当x为何值时,y随x的增大而减小?
成果集成
1.抛物线的图象性质
2.在同一直角坐标系中探究二次函数开口大小与 的关系
下课!
同学们,再见!
