5.6二次函数与一元二次方程 课件(共14张PPT) 2022-2023学年青岛版九年级数学下册
文档属性
| 名称 | 5.6二次函数与一元二次方程 课件(共14张PPT) 2022-2023学年青岛版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 419.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-18 11:21:20 | ||
图片预览






文档简介
(共14张PPT)
5.6二次函数与一元二次方程
今天与明天
今天再晚也是早
明天再早也是晚
把握今天成就明天
课标要求
1.会利用二次函数的图像求一元二次方程的近似解。2.二次函数的图象与x轴交点与一元二次方程的根之间的关系;3.培养学生的数形结合思想和建模意识.
学习目标
1.通过观察二次函数图象,说出二次函数图象与x轴交点的个数与对应的一元二次方程的根的个数之间的关系;
2.通过典型例题分析归纳出一元二次方程a +bx+c=h的根就是二次函数
y=a +bx+c 与直线y=h(h是实数)图象交点的横坐标.
达成评价
1.能探究出二次函数y=a +bx+c的图象与x轴交点与一元二次方程a +bx+c=0方程的根之间的关系.
2.能够利用一元二次方a +bx+c=h的根就是二次函数y=a +bx+c 与直线y=h(h是实数)图象交点的横坐标来解决问题.
先行组织
1.方程 +2x- 3=0的解是 ————
2.抛物线y = +2x- 3与x轴的交点坐标是__________ .
3.一元二次方程 ,
当Δ 时,方程有两个不相等的实数根;
当Δ 时,方程有两个相等的实数根;
当Δ 时,方程没有实数根;
4.二次函数 的图像与x轴的交点有几种可能情况?
5.我想问的问题:_______________________________________________.
任务一:探索二次函数图像与一元二次方程的关系
活动1:观察抛物线 ,思考下面的问题:
y=
(1)比较二次函数的表达式 与一元二次方程 ,你能 说出二者有什么联系吗?
(2) 一元二次方程 的实数根是________.
(3)抛物线 与 x 轴有______个公共点?交点的坐标分别为_________、_________.
(4)一元二次方程 的实数根和抛物线 与x 轴的公共点的横坐标有什么关系?
(5)思考:一元二次方程 的根与抛物线 与 x轴交点的横坐标有什么关系?
任务一:探索二次函数图像与一元二次方程的关系
知识归纳:如果一元二次方程 有实根,那么二次函数 的图象与x轴有公共点,且公共点的横坐标是这个一元二次方程的实根; 反之,二次函数 的图象与 x轴有公共点,那么公共点的横坐标就是一元二次方程 的实数根.
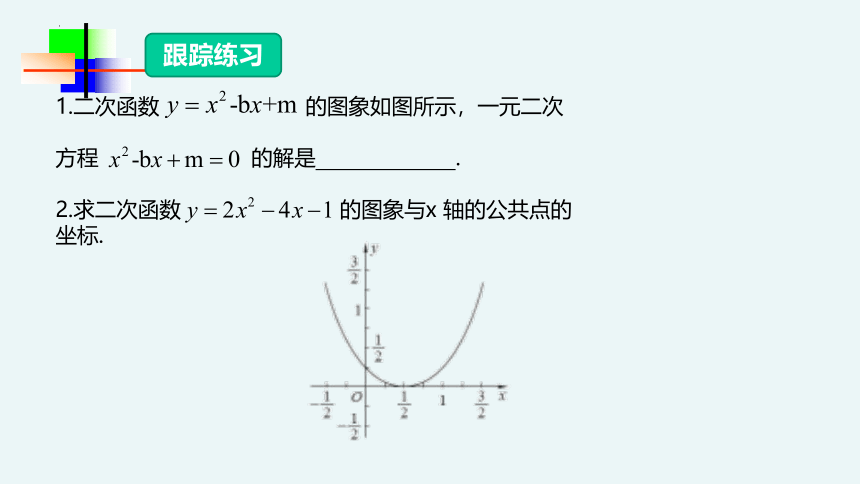
跟踪练习
1.二次函数 的图象如图所示,一元二次
方程 的解是 .
2.求二次函数 的图象与x 轴的公共点的坐标.
任务二:二次函数的图像与一元二次不等式的关系
1.二次函数 的图像如图所示:
(1) 当 x 时, ? 当x 时, ?
(2)利用图像写出不等式 的解集是 .
跟踪练习
1.根据下面的图像,说出一元二次不等式 的解集.
2.根据下面的图像,说出一元二次不等式 的解集.
任务三:a、b、c、b2-4ac符号及相关代数式符号的判定
1.已知二次函数的图象如图所示,判断下列各式的符号:
a___0, b___0, c___0, b2-4ac____0,
a+b+c____0, a-b+c____0.
2.分析试题:
(1)抛物线开口向下可得a﹤0
(2)由抛物线的对称轴 ,可得 ,得出 a、b异号,
∵a﹤0 ∴b﹥0
由上面的推导得出规律:
对称轴在右侧 a、b异号
对称轴在左侧 a、b同号
(3)由抛物线交于y轴正半轴可得c﹥0
(4)由抛物线与x轴有两个交点可得 ﹥0
(5)取x=1时,y=a+b+c,∵x=1时y﹥0,∴a+b+c﹥0
迁移运用
如果关于x的一元二次方程ax2+2x-5=0的两根中恰有一个根大于0而小于1,求a的取值范围.
成果集成
教师引导学生从知识、应用、启示方面总结收获.
通过本节课的学习你有什么收获?
作业设计
1.(C层)不论x取何值抛物线 总在x轴上方,则a,b,c满足的条件是( )
A. B. C. D.
2.(B层)已知二次函数.
(1)当实数k为何值时,图象经过原点?
(2)当实数k在何范围取值时,函数图象的顶点在第四象限内
3.(A层)如图,二次函数的图象与x轴交于B、C两点,交y轴于点A.(1)根据图象确定a,b,c的符号;(2)如果OC=OA= ,
BC=4,求这个二次函数的解析式.
B
O
A
C
x
y
下课!
同学们,再见!
5.6二次函数与一元二次方程
今天与明天
今天再晚也是早
明天再早也是晚
把握今天成就明天
课标要求
1.会利用二次函数的图像求一元二次方程的近似解。2.二次函数的图象与x轴交点与一元二次方程的根之间的关系;3.培养学生的数形结合思想和建模意识.
学习目标
1.通过观察二次函数图象,说出二次函数图象与x轴交点的个数与对应的一元二次方程的根的个数之间的关系;
2.通过典型例题分析归纳出一元二次方程a +bx+c=h的根就是二次函数
y=a +bx+c 与直线y=h(h是实数)图象交点的横坐标.
达成评价
1.能探究出二次函数y=a +bx+c的图象与x轴交点与一元二次方程a +bx+c=0方程的根之间的关系.
2.能够利用一元二次方a +bx+c=h的根就是二次函数y=a +bx+c 与直线y=h(h是实数)图象交点的横坐标来解决问题.
先行组织
1.方程 +2x- 3=0的解是 ————
2.抛物线y = +2x- 3与x轴的交点坐标是__________ .
3.一元二次方程 ,
当Δ 时,方程有两个不相等的实数根;
当Δ 时,方程有两个相等的实数根;
当Δ 时,方程没有实数根;
4.二次函数 的图像与x轴的交点有几种可能情况?
5.我想问的问题:_______________________________________________.
任务一:探索二次函数图像与一元二次方程的关系
活动1:观察抛物线 ,思考下面的问题:
y=
(1)比较二次函数的表达式 与一元二次方程 ,你能 说出二者有什么联系吗?
(2) 一元二次方程 的实数根是________.
(3)抛物线 与 x 轴有______个公共点?交点的坐标分别为_________、_________.
(4)一元二次方程 的实数根和抛物线 与x 轴的公共点的横坐标有什么关系?
(5)思考:一元二次方程 的根与抛物线 与 x轴交点的横坐标有什么关系?
任务一:探索二次函数图像与一元二次方程的关系
知识归纳:如果一元二次方程 有实根,那么二次函数 的图象与x轴有公共点,且公共点的横坐标是这个一元二次方程的实根; 反之,二次函数 的图象与 x轴有公共点,那么公共点的横坐标就是一元二次方程 的实数根.
跟踪练习
1.二次函数 的图象如图所示,一元二次
方程 的解是 .
2.求二次函数 的图象与x 轴的公共点的坐标.
任务二:二次函数的图像与一元二次不等式的关系
1.二次函数 的图像如图所示:
(1) 当 x 时, ? 当x 时, ?
(2)利用图像写出不等式 的解集是 .
跟踪练习
1.根据下面的图像,说出一元二次不等式 的解集.
2.根据下面的图像,说出一元二次不等式 的解集.
任务三:a、b、c、b2-4ac符号及相关代数式符号的判定
1.已知二次函数的图象如图所示,判断下列各式的符号:
a___0, b___0, c___0, b2-4ac____0,
a+b+c____0, a-b+c____0.
2.分析试题:
(1)抛物线开口向下可得a﹤0
(2)由抛物线的对称轴 ,可得 ,得出 a、b异号,
∵a﹤0 ∴b﹥0
由上面的推导得出规律:
对称轴在右侧 a、b异号
对称轴在左侧 a、b同号
(3)由抛物线交于y轴正半轴可得c﹥0
(4)由抛物线与x轴有两个交点可得 ﹥0
(5)取x=1时,y=a+b+c,∵x=1时y﹥0,∴a+b+c﹥0
迁移运用
如果关于x的一元二次方程ax2+2x-5=0的两根中恰有一个根大于0而小于1,求a的取值范围.
成果集成
教师引导学生从知识、应用、启示方面总结收获.
通过本节课的学习你有什么收获?
作业设计
1.(C层)不论x取何值抛物线 总在x轴上方,则a,b,c满足的条件是( )
A. B. C. D.
2.(B层)已知二次函数.
(1)当实数k为何值时,图象经过原点?
(2)当实数k在何范围取值时,函数图象的顶点在第四象限内
3.(A层)如图,二次函数的图象与x轴交于B、C两点,交y轴于点A.(1)根据图象确定a,b,c的符号;(2)如果OC=OA= ,
BC=4,求这个二次函数的解析式.
B
O
A
C
x
y
下课!
同学们,再见!
