6.2.3 组合(1) 课件(共31张PPT)
文档属性
| 名称 | 6.2.3 组合(1) 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 453.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 23:09:55 | ||
图片预览











文档简介
(共31张PPT)
6.2.3 组合(1)
问题一: 从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法?
问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?
甲、乙; 甲、丙; 乙、丙
3
新知探究
从已知的 3个不同元素中每次取出2个元素合成一组
问题2
从已知的3 个不同元素 中每次取出2个元素,按照一定的顺序排成一列.
问题1
排列
组合
有
顺
序
无
顺
序
新知探究
1).组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素合成一组,叫做从n个不同元素中取出m个元素的一个组合.
排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元 素中取出 m 个元素的一个排列.
共同点: 都要“从n个不同元素中任取m个元素”
不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.
2).组合和排列有什么共同和不同点
组合
甲乙
甲丙
乙丙
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
排列
新知探究
判断下列问题是组合问题还是排列问题
(1).设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个
(2).某铁路线上有5个车站,则这条铁路线上共需准备多少种车票
有多少种不同的火车票价
组合问题
排列问题
(3).10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法
组合问题
组合问题
组合是选择的结果,
排列是选择后再排序的结果.
新知探究
(4).10人聚会,见面后每两人之间要握手相互问候, 共需握手多少次
组合问题
(5).从4个风景点中选出2个游览,有多少种不同的方法
组合问题
(6).从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法
排列问题
(7).校门口停放着9辆共享自行车,其中黄色、红色、绿色的各3辆.
①.从中选3辆,有多少种不同的方法
②.从中选3辆给3位同学,有多少种不同的方法
组合问题
排列问题
新知探究
例5.平面内有A、B、C、D共4个点.
(1).以其中2个点为端点的有向线段共有多少条
(2).以其中2个点为端点的线段共有多少条
分析: (1).确定一条有向线段,不仅要确定两个端点,还要考虑它们的顺序,是排列问题; (2).确定一条线段,只需确定两个端点,而不考虑它们的顺序,是组合问题.
新知探究
解:(1). 一条有向线段的端点要分起点和端点,以平面内4个 点中的两个点为端点的有向线段的条数,就是从4个元素中取出2个元素的排列数,共有 条.
(2). 将(1)中端点相同、方向不同的2条有向线段作为1条线段,就是以平面内4个点中的2个点为端点的线段的条数,共有如下6条:AB,AC,AD,BC,BD,CD.
新知探究
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数.
用符号 表示.
组合数:
注意:
是一个数,应该把它与“组合”区别开来.
新知探究
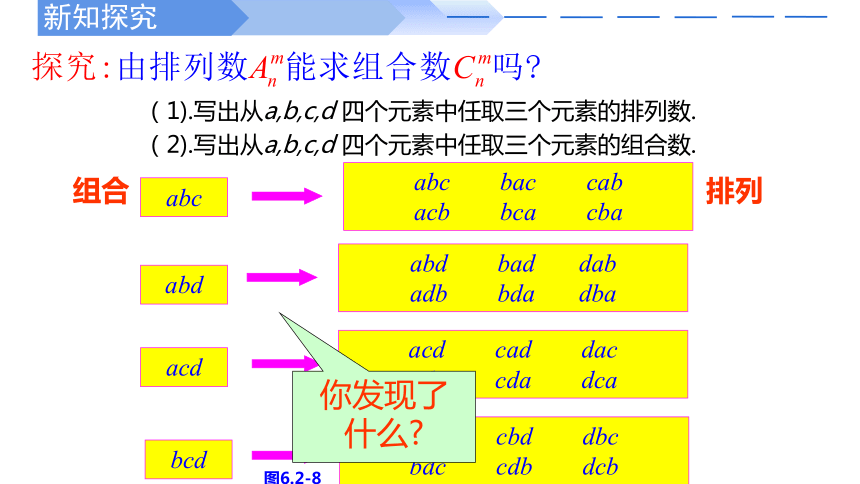
组合
排列
abc
abd
acd
bcd
abc bac cab
acb bca cba
abd bad dab
adb bda dba
acd cad dac
adc cda dca
bcd cbd dbc
bdc cdb dcb
你发现了
什么
(1).写出从a,b,c,d 四个元素中任取三个元素的排列数.(2).写出从a,b,c,d 四个元素中任取三个元素的组合数.
图6.2-8
新知探究
根据分步计数原理,得到:
因此:
一般地,求从 n个不同元素中取出 m 个元素的排列数可以分为以下2步:
第1步,先求出从这 个不同元素中取出 个 元素的组合数 .
第2步,求每一个组合中 个元素的全排列数 .
这里 , 且 ,这个公式叫做组合数公式.
新知探究
组合数公式:
从 n 个不同元中取出m个元素的排列数
组合数公式:
新知探究
例6.计算:
观察上面计算的结果,你有什么发现
新知探究
组合数的性质:
新知探究
证明性质2:
新知探究
巩固应用:
1).计算:
2).解方程:
3).计算:
4或7
新知探究
1.从a,b,c三个不同的元素中任取两个元素的组合有6个. ( )
提示 从a,b,c三个不同的元素中任取两个元素的组合有{a,b},{a,c},{b,c}3个.
2.从1,3,5,7中任取两个数相乘可得6个积. ( )
3.1,2,3与3,2,1是同一个组合. ( )
×
√
√
辨析
1.下列问题属于组合问题的是________.
①由1,2,3,4构成的双元素集合;②由1,2,3构成的两位数的方法;③由1,2,3组成无重复数字的两位数的方法.
答案 ①
2.甲、乙、丙三地之间有直达的火车,相互之间距离均不相等,则车票票价的种数是____(假设票价只与距离有关).
答案 3
新知探索
两个相同的排列有什么特点?两个相同的组合呢?
提示 两个相同的排列需元素相同且元素排列顺序相同.两个相同的组合只要元素相同,不看元素顺序如何.
新知探索
题型一 组合概念的理解
【例1】 (多空题)给出下列问题:
(1)a,b,c,d四支足球队之间进行单循环比赛,共需比赛多少场?
(2)a,b,c,d四支足球队争夺冠、亚军,有多少种不同的结果?
(3)从全班40人中选出3人分别担任班长、副班长、学习委员三个职务,有多少种不同的选法?
(4)从全班40人中选出3人参加某项活动,有多少种不同的选法?
在上述问题中,____是组合问题,______是排列问题.
练习巩固
解析 (1)单循环比赛要求两支球队之间只打一场比赛,没有顺序,是组合问题.
(2)冠、亚军是有顺序的,是排列问题.
(3)3人分别担任三个不同职务,有顺序,是排列问题.
(4)3人参加某项相同活动,没有顺序,是组合问题.
答案 (1)(4) (2)(3)
练习巩固
规律方法 区分排列与组合的办法是首先弄清楚事件是什么,区分的标志是有无顺序,而区分有无顺序的方法是:把问题的一个选择结果写出来,然后交换这个结果中任意两个元素的位置,看是否产生新的变化,若有新变化,即说明有顺序,是排列问题;若无新变化,即说明无顺序,是组合问题.
练习巩固
变1 判断下列问题是排列问题还是组合问题.
(1)集合{0,1,2,3,4}的含三个元素的子集的个数是多少?
(2)某小组有9位同学,从中选出正、副班长各一个,有多少种不同的选法?若从中选出2名代表参加一个会议,有多少种不同的选法?
解 (1)由于集合中的元素是不讲次序的,一个含三个元素的集合就是一个从0,1,2,3,4中取出3个数组成的集合.这是一个组合问题.
(2)选正、副班长时要考虑次序,所以是排列问题;选代表参加会议是不用考虑次序的,所以是组合问题.
练习巩固
题型二 简单的组合问题
【例2】 (多空题)有5名教师,其中3名男教师,2名女教师.
(1)现要从中选2名去参加会议,有__________种不同的选法;
(2)选出2名男教师或2名女教师参加会议,有________种不同的选法;
(3)现要从中选出男、女教师各2名去参加会议,有__________种不同的选法.
练习巩固
解析 (1)从5名教师中选2名去参加会议的选法种数,通过列举法可得共有10种不同的方法.
(2)可把问题分两类情况:
第1类,选出的2名是男教师,有3种方法;
第2类,选出的2名是女教师,有1种方法.
根据分类加法计数原理,共有3+1=4(种)不同选法.
(3)从3名男教师中选2名的选法有3种,从2名女教师中选2名的选法有1种,根据分步乘法计数原理,共有不同的选法3×1=3(种).
答案 (1)10 (2)4 (3)3
练习巩固
规律方法 (1)解简单的组合应用题时,首先要判断它是不是组合问题,组合问题与排列问题的根本区别在于排列问题与取出元素之间的顺序有关,而组合问题与取出元素的顺序无关.
(2)要注意两个基本原理的运用,即分类与分步的灵活运用.
在分类和分步时,一定注意有无重复或遗漏.
练习巩固
变2 一个口袋内装有大小相同的4个白球和1个黑球.
(1)从口袋内取出的3个小球,共有多少种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?
解 (1)从口袋内的5个球中取出3个球,取法种数是10.
(2)从口袋内取出3个球有1个是黑球,于是需要从4个白球中取出2个,取法种数是6.
(3)由于所取出的3个球中不含黑球,也就是要从4个白球中取出3个球,取法种数是4.
练习巩固
题型三 双重元素的组合问题
【例3】 某中学要从4名男生和3名女生中选4人参加公益活动,若男生甲和女生乙不能同时参加,则不同的选派方案共有( )
A.25种 B.35种
C.820种 D.840种
解析 分3类完成:男生甲参加,女生乙不参加,只需在其余5人中选3人,有10种选法;男生甲不参加,女生乙参加,只需在其余5人中选3人,有10种选法;两人都不参加,只需在其余5人中选4人,有5种选法.所以共有10+10+5=25(种)不同的选派方案.
答案 A
练习巩固
规律方法 本题用到两个计数原理解题,两个原理的区别在于:前者每次得到的是最后结果,后者每次得到的是中间结果,即每次仅完成整件事情的一部分,当且仅当几个步骤全部做完后,整件事情才算完成.
练习巩固
变3 某校开设A类选修课3门,B类选修课5门,一位同学要从中选3门.若要求两类课程中各至少选1门,则不同的选法共有( )
A.15种 B.30种 C.45种 D.90种
解析 分两类,A类选修课选1门,B选修课选2门,或者A类选修课选2门,B类选修课选1门,因此,共有3×10+3×5=45(种)选法.
答案 C
练习巩固
课堂小结
1.组合定义:
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
2.组合数:
3.组合数公式:
6.2.3 组合(1)
问题一: 从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法?
问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?
甲、乙; 甲、丙; 乙、丙
3
新知探究
从已知的 3个不同元素中每次取出2个元素合成一组
问题2
从已知的3 个不同元素 中每次取出2个元素,按照一定的顺序排成一列.
问题1
排列
组合
有
顺
序
无
顺
序
新知探究
1).组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素合成一组,叫做从n个不同元素中取出m个元素的一个组合.
排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元 素中取出 m 个元素的一个排列.
共同点: 都要“从n个不同元素中任取m个元素”
不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.
2).组合和排列有什么共同和不同点
组合
甲乙
甲丙
乙丙
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
排列
新知探究
判断下列问题是组合问题还是排列问题
(1).设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个
(2).某铁路线上有5个车站,则这条铁路线上共需准备多少种车票
有多少种不同的火车票价
组合问题
排列问题
(3).10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法
组合问题
组合问题
组合是选择的结果,
排列是选择后再排序的结果.
新知探究
(4).10人聚会,见面后每两人之间要握手相互问候, 共需握手多少次
组合问题
(5).从4个风景点中选出2个游览,有多少种不同的方法
组合问题
(6).从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法
排列问题
(7).校门口停放着9辆共享自行车,其中黄色、红色、绿色的各3辆.
①.从中选3辆,有多少种不同的方法
②.从中选3辆给3位同学,有多少种不同的方法
组合问题
排列问题
新知探究
例5.平面内有A、B、C、D共4个点.
(1).以其中2个点为端点的有向线段共有多少条
(2).以其中2个点为端点的线段共有多少条
分析: (1).确定一条有向线段,不仅要确定两个端点,还要考虑它们的顺序,是排列问题; (2).确定一条线段,只需确定两个端点,而不考虑它们的顺序,是组合问题.
新知探究
解:(1). 一条有向线段的端点要分起点和端点,以平面内4个 点中的两个点为端点的有向线段的条数,就是从4个元素中取出2个元素的排列数,共有 条.
(2). 将(1)中端点相同、方向不同的2条有向线段作为1条线段,就是以平面内4个点中的2个点为端点的线段的条数,共有如下6条:AB,AC,AD,BC,BD,CD.
新知探究
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数.
用符号 表示.
组合数:
注意:
是一个数,应该把它与“组合”区别开来.
新知探究
组合
排列
abc
abd
acd
bcd
abc bac cab
acb bca cba
abd bad dab
adb bda dba
acd cad dac
adc cda dca
bcd cbd dbc
bdc cdb dcb
你发现了
什么
(1).写出从a,b,c,d 四个元素中任取三个元素的排列数.(2).写出从a,b,c,d 四个元素中任取三个元素的组合数.
图6.2-8
新知探究
根据分步计数原理,得到:
因此:
一般地,求从 n个不同元素中取出 m 个元素的排列数可以分为以下2步:
第1步,先求出从这 个不同元素中取出 个 元素的组合数 .
第2步,求每一个组合中 个元素的全排列数 .
这里 , 且 ,这个公式叫做组合数公式.
新知探究
组合数公式:
从 n 个不同元中取出m个元素的排列数
组合数公式:
新知探究
例6.计算:
观察上面计算的结果,你有什么发现
新知探究
组合数的性质:
新知探究
证明性质2:
新知探究
巩固应用:
1).计算:
2).解方程:
3).计算:
4或7
新知探究
1.从a,b,c三个不同的元素中任取两个元素的组合有6个. ( )
提示 从a,b,c三个不同的元素中任取两个元素的组合有{a,b},{a,c},{b,c}3个.
2.从1,3,5,7中任取两个数相乘可得6个积. ( )
3.1,2,3与3,2,1是同一个组合. ( )
×
√
√
辨析
1.下列问题属于组合问题的是________.
①由1,2,3,4构成的双元素集合;②由1,2,3构成的两位数的方法;③由1,2,3组成无重复数字的两位数的方法.
答案 ①
2.甲、乙、丙三地之间有直达的火车,相互之间距离均不相等,则车票票价的种数是____(假设票价只与距离有关).
答案 3
新知探索
两个相同的排列有什么特点?两个相同的组合呢?
提示 两个相同的排列需元素相同且元素排列顺序相同.两个相同的组合只要元素相同,不看元素顺序如何.
新知探索
题型一 组合概念的理解
【例1】 (多空题)给出下列问题:
(1)a,b,c,d四支足球队之间进行单循环比赛,共需比赛多少场?
(2)a,b,c,d四支足球队争夺冠、亚军,有多少种不同的结果?
(3)从全班40人中选出3人分别担任班长、副班长、学习委员三个职务,有多少种不同的选法?
(4)从全班40人中选出3人参加某项活动,有多少种不同的选法?
在上述问题中,____是组合问题,______是排列问题.
练习巩固
解析 (1)单循环比赛要求两支球队之间只打一场比赛,没有顺序,是组合问题.
(2)冠、亚军是有顺序的,是排列问题.
(3)3人分别担任三个不同职务,有顺序,是排列问题.
(4)3人参加某项相同活动,没有顺序,是组合问题.
答案 (1)(4) (2)(3)
练习巩固
规律方法 区分排列与组合的办法是首先弄清楚事件是什么,区分的标志是有无顺序,而区分有无顺序的方法是:把问题的一个选择结果写出来,然后交换这个结果中任意两个元素的位置,看是否产生新的变化,若有新变化,即说明有顺序,是排列问题;若无新变化,即说明无顺序,是组合问题.
练习巩固
变1 判断下列问题是排列问题还是组合问题.
(1)集合{0,1,2,3,4}的含三个元素的子集的个数是多少?
(2)某小组有9位同学,从中选出正、副班长各一个,有多少种不同的选法?若从中选出2名代表参加一个会议,有多少种不同的选法?
解 (1)由于集合中的元素是不讲次序的,一个含三个元素的集合就是一个从0,1,2,3,4中取出3个数组成的集合.这是一个组合问题.
(2)选正、副班长时要考虑次序,所以是排列问题;选代表参加会议是不用考虑次序的,所以是组合问题.
练习巩固
题型二 简单的组合问题
【例2】 (多空题)有5名教师,其中3名男教师,2名女教师.
(1)现要从中选2名去参加会议,有__________种不同的选法;
(2)选出2名男教师或2名女教师参加会议,有________种不同的选法;
(3)现要从中选出男、女教师各2名去参加会议,有__________种不同的选法.
练习巩固
解析 (1)从5名教师中选2名去参加会议的选法种数,通过列举法可得共有10种不同的方法.
(2)可把问题分两类情况:
第1类,选出的2名是男教师,有3种方法;
第2类,选出的2名是女教师,有1种方法.
根据分类加法计数原理,共有3+1=4(种)不同选法.
(3)从3名男教师中选2名的选法有3种,从2名女教师中选2名的选法有1种,根据分步乘法计数原理,共有不同的选法3×1=3(种).
答案 (1)10 (2)4 (3)3
练习巩固
规律方法 (1)解简单的组合应用题时,首先要判断它是不是组合问题,组合问题与排列问题的根本区别在于排列问题与取出元素之间的顺序有关,而组合问题与取出元素的顺序无关.
(2)要注意两个基本原理的运用,即分类与分步的灵活运用.
在分类和分步时,一定注意有无重复或遗漏.
练习巩固
变2 一个口袋内装有大小相同的4个白球和1个黑球.
(1)从口袋内取出的3个小球,共有多少种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?
解 (1)从口袋内的5个球中取出3个球,取法种数是10.
(2)从口袋内取出3个球有1个是黑球,于是需要从4个白球中取出2个,取法种数是6.
(3)由于所取出的3个球中不含黑球,也就是要从4个白球中取出3个球,取法种数是4.
练习巩固
题型三 双重元素的组合问题
【例3】 某中学要从4名男生和3名女生中选4人参加公益活动,若男生甲和女生乙不能同时参加,则不同的选派方案共有( )
A.25种 B.35种
C.820种 D.840种
解析 分3类完成:男生甲参加,女生乙不参加,只需在其余5人中选3人,有10种选法;男生甲不参加,女生乙参加,只需在其余5人中选3人,有10种选法;两人都不参加,只需在其余5人中选4人,有5种选法.所以共有10+10+5=25(种)不同的选派方案.
答案 A
练习巩固
规律方法 本题用到两个计数原理解题,两个原理的区别在于:前者每次得到的是最后结果,后者每次得到的是中间结果,即每次仅完成整件事情的一部分,当且仅当几个步骤全部做完后,整件事情才算完成.
练习巩固
变3 某校开设A类选修课3门,B类选修课5门,一位同学要从中选3门.若要求两类课程中各至少选1门,则不同的选法共有( )
A.15种 B.30种 C.45种 D.90种
解析 分两类,A类选修课选1门,B选修课选2门,或者A类选修课选2门,B类选修课选1门,因此,共有3×10+3×5=45(种)选法.
答案 C
练习巩固
课堂小结
1.组合定义:
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
2.组合数:
3.组合数公式:
