平行四边形中考训练题

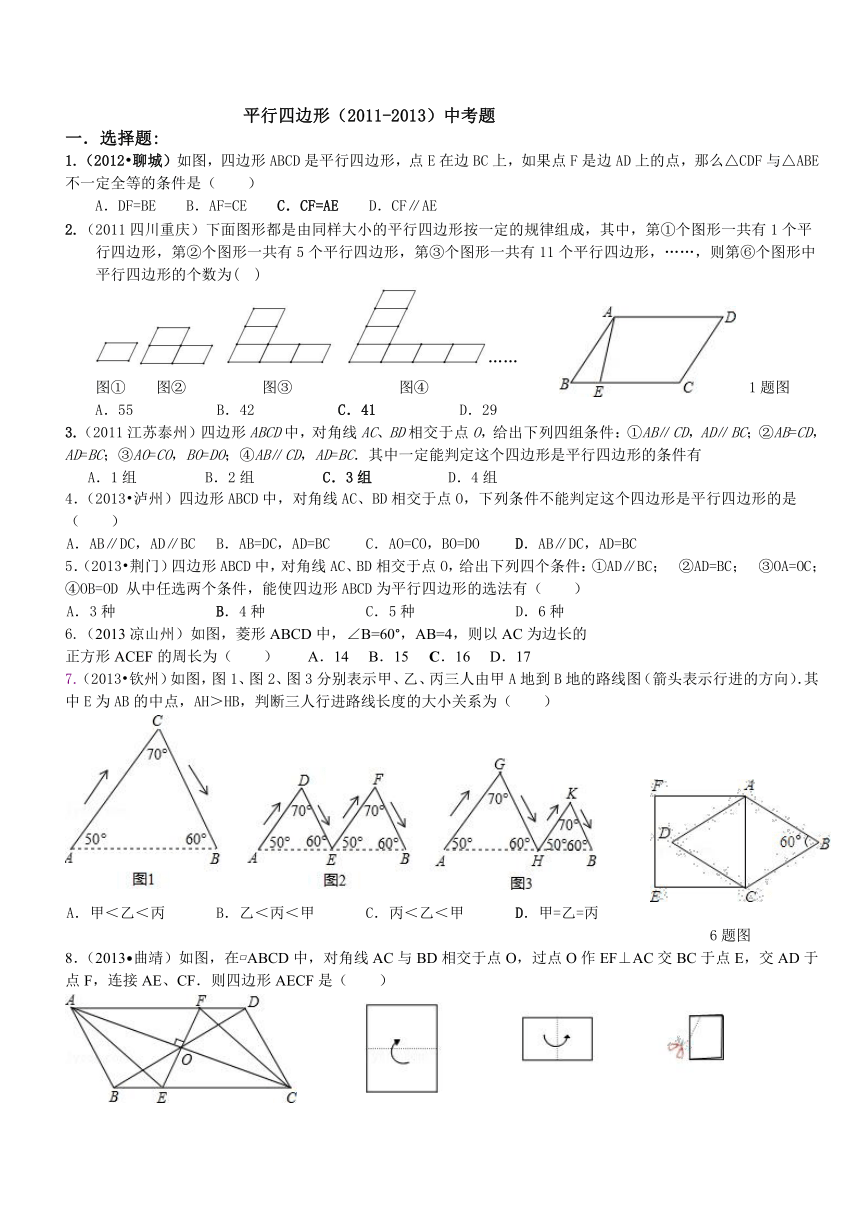
平行四边形（2011-2013）中考题
一．选择题:
1.（2012 聊城）如图，四边形ABCD是平行四边形，点E在边BC上，如果点F是边AD上的点，那么△CDF与△ABE不一定全等的条件是（　　）
　　A．DF=BE　　B．AF=CE　　C．CF=AE　　D．CF∥AE
2.（2011四川重庆）下面图形都是由同样大小的平行四边形按一定的规律组成，其中，第①个图形一共有1个平行四边形，第②个图形一共有5个平行四边形，第③个图形一共有11个平行四边形，……，则第⑥个图形中平行四边形的个数为( )
……
图① 图② 图③ 图④ 1题图
A．55 B．42 C．41 D．29
3.（2011江苏泰州）四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC．其中一定能判定这个四边形是平行四边形的条件有
A．1组 B．2组 C．3组 D．4组
4．（2013 泸州）四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（　　）
　 A． AB∥DC，AD∥BC B． AB=DC，AD=BC C． AO=CO，BO=DO D． AB∥DC，AD=BC
5．（2013 荆门）四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC； ②AD=BC； ③OA=OC； ④OB=OD 从中任选两个条件，能使四边形ABCD为平行四边形的选法有（　　）
　 A． 3种 B． 4种 C． 5种 D． 6种
6.（2013凉山州）如图，菱形ABCD中，∠B=60°，AB=4，则以AC为边长的
正方形ACEF的周长为（　　） A．14 B．15 C．16 D．17
7.（2013 钦州）如图，图1、图2、图3分别表示甲、乙、丙三人由甲A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AH＞HB，判断三人行进路线长度的大小关系为（　　）
　 A． 甲＜乙＜丙 B． 乙＜丙＜甲 C． 丙＜乙＜甲 D． 甲=乙=丙
6题图
8．（2013 曲靖）如图，在 ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE、CF．则四边形AECF是（　　）
　 A． 梯形 B． 矩形 C． 菱形 D． 正方形
9．（2013菏泽）如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为120° 的菱形，剪口与第二次折痕所成角的度数应为（　　）
　 A．15°或30° B．30°或45° C．45°或60° D．30°或60°
10．（2013 玉林）如图，在给定的一张平行四边形纸片上作一个菱形．甲、乙两人的作法如下：
甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形．根据两人的作法可判断（　　）
　 A． 甲正确，乙错误 B． 乙正确，甲错误 C． 甲、乙均正确 D． 甲、乙均错误
11．（2013 包头）如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是（　　）
A． S1＞S2 B． S1=S2 C． S1＜S2 D． 3S1=2S2
12．（2013台湾）如图，长方形ABCD中，M为CD中点，今以B、M为圆心，分别以BC长、MC长为半径画弧，两弧相交于P点．若∠PBC=70°，则∠MPC的度数为何？（　　）A．20 B．35 C．40 D．55
二．填空题：
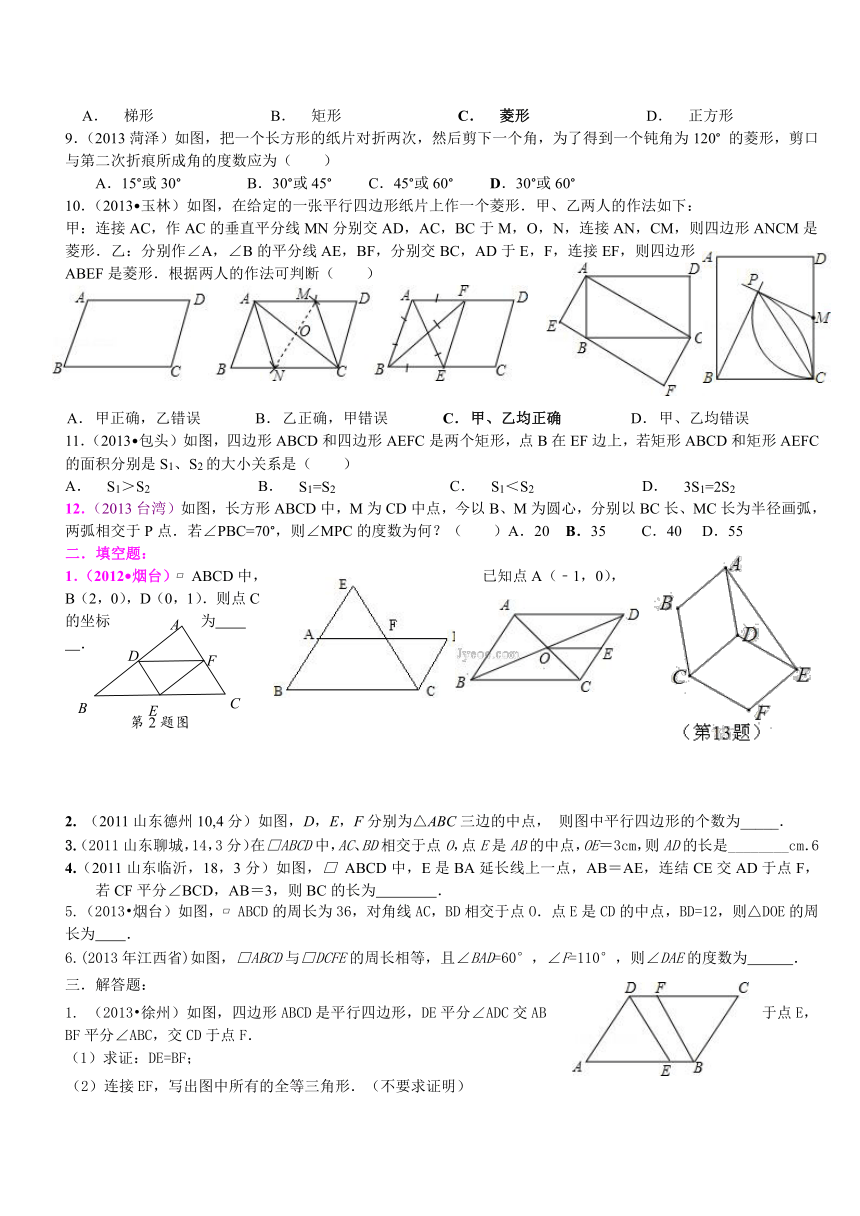
1．（2012 烟台） ABCD中，已知点A（﹣1，0），B（2，0），D（0，1）．则点C的坐标为　 　．
2. （2011山东德州10,4分）如图，D，E，F分别为△ABC三边的中点， 则图中平行四边形的个数为_____．
3.（2011山东聊城，14，3分）在□ABCD中，AC、BD相交于点O，点E是AB的中点，OE＝3cm，则AD的长是________cm．6
4.（2011山东临沂，18，3分）如图，□ ABCD中，E是BA延长线上一点，AB＝AE，连结CE交AD于点F，若CF平分∠BCD，AB＝3，则BC的长为 ．
5.（2013 烟台）如图， ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，则△DOE的周长为　　．
6.(2013年江西省)如图，□ABCD与□DCFE的周长相等，且∠BAD=60°，∠F=110°，则∠DAE的度数为 ．
三．解答题：
1. （2013 徐州）如图，四边形ABCD是平行四边形，DE平分∠ADC交AB于点E，BF平分∠ABC，交CD于点F．
（1）求证：DE=BF；
（2）连接EF，写出图中所有的全等三角形．（不要求证明）
2. （2012泰州)如图，四边形ABCD中，AD∥BC,AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE=CF.求证：四边形ABCD是平行四边形．
3. （2013 新疆）如图， ABCD中，点O是AC与BD的交点，过点O的直线与BA、DC的延长线分别交于点E、F．
（1）求证：△AOE≌△COF；
（2）请连接EC、AF，则EF与AC满足什么条件时，四边形AECF是矩形，
并说明理由．
4．（2011四川宜宾,17⑶,5分）如图，平行四边形ABCD的对角线AC、BD交于点O，E、F在AC上，G、H在BD上，AF=CE，BH=DG．
求证：GF∥HE．
5. （2013 莱芜）如图，在Rt△ABC中，∠C=90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连结DE．
（1）证明DE∥CB；
（2）探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．
参考答案：一、C C C D B C D C D C B B
二、 1.（3，1） 2.. 3 3. 6 4.6 5. 15 6. 15
三、1. 证明：（1）∵四边形ABCD是平行四边形，
∴DC∥AB∴∠CDE=∠AED， ∵DE平分∠ADC， ∴∠ADE=∠CDE， ∴∠ADE=∠AED，∴AE=AD，
同理CF=CB，又AD=CB，AB=CD， ∴AE=CF， ∴DF=BE， ∴四边形DEBF是平行四边形， ∴DE=BF，
（2）△ADE≌△CBF，△DFE≌△BEF．
2. 【解析】要证四边形ABCD是平行四边形．只要证AD=CB，需证△AED≌△FCB，结合易知证明就较为简单．
【答案】∵AD∥BC,∴∠ADE=∠CBF，又∠DAE=∠BCF=900，∴△AED≌△FCB，∴AD=BC，∴四边形ABCD是平行四边形．
3. （1）证明：∵四边形ABCD是平行四边形，
∴AO=OC，AB∥CD． ∴∠E=∠F又∠AOE=∠COF． ∴△AOE≌△COF（ASA）；
（2）连接EC、AF，则EF与AC满足EF=AC时，四边形AECF是矩形，
理由如下： 由（1）可知△AOE≌△COF， ∴OE=OF， ∵AO=CO，
∴四边形AECF是平行四边形， ∵EF=AC，
∴四边形AECF是矩形
4.证明：∵平行四边形ABCD中，OA=OC，
由已知：AF=CE
AF－OA=CE－OC ∴OF=OE
同理得：OG=OH
∴四边形EGFH是平行四边形
5. （1）证明：连结CE． ∵点E为Rt△ACB的斜边AB的中点，
∴CE=AB=AE． ∵△ACD是等边三角形， ∴AD=CD．
在△ADE与△CDE中，
∵AD=DC, DE=DE, AE=CE
∴△ADE≌△CDE（SSS）， ∴∠ADE=∠CDE=30°．
∵∠DCB=150°， ∴∠EDC+∠DCB=180°．
∴DE∥CB．
（2）解：∵∠DCB=150°，若四边形DCBE是平行四边形，
则DC∥BE，∠DCB+∠B=180°． ∴∠B=30°． 在Rt△ACB中，AB=2AC．
∴当AB=2AC时，四边形DCBE是平行四边形
A
B
C
D
E
F
第2题图
H
A
C
B
D
O
E
G
F