6 扇形(课件)六年级上册数学人教版(共19张PPT)
文档属性
| 名称 | 6 扇形(课件)六年级上册数学人教版(共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 950.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
6 扇形
第五单元 圆
1.认识弧、圆心角以及它们间的对应关系,掌握扇形的基本特征,能准确判别扇形,知道圆心角及半径的大小决定扇形的大小。
2.在观察、比较、讨论、判断等活动中,初步经历认识扇形的过程,通过比一比、画一画等操作活动,提高动手操作、与人合作的能力。
3.在体会扇形和圆的密切联系中感受数学知识之间的内在联系。
温习旧知
一、求下图阴影部分的周长和面积。(单位:dm)
周长:3.14×10×2=62.8(dm)
面积:3.14×(10÷2)2÷2×4-10×10=57(dm2)
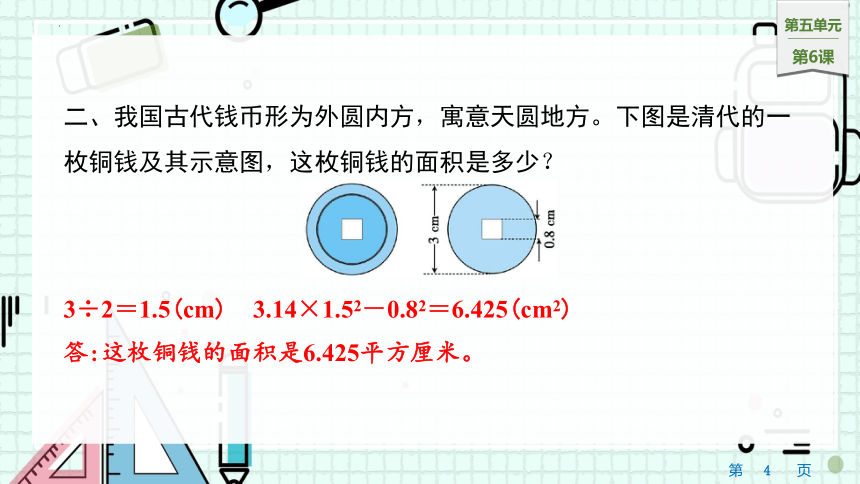
二、我国古代钱币形为外圆内方,寓意天圆地方。下图是清代的一枚铜钱及其示意图,这枚铜钱的面积是多少?
3÷2=1.5(cm) 3.14×1.52-0.82=6.425(cm2)
答:这枚铜钱的面积是6.425平方厘米。
知识链接
气象学家洛伦兹写了一篇论文,标题为《一只蝴蝶拍一下翅膀会不会在得克萨斯州引起龙卷风》,论述某系统如果初期条件差一点点,结果会很不稳定,他把这种现象称作“蝴蝶效应”。就像我们投掷骰子两次,无论如何刻意去投掷,投出的点数都不一定是相同的。
预习新知
一、课前自学扇形,完成温习旧知,初步认识扇形、圆心角、弧。
二、课堂中和同学合作交流什么是扇形,扇形的面积和什么有关,合作探究如何求扇形的面积。
三、课堂中和老师一起认识扇形、圆心角、弧,能正确辨认扇形和圆心角,总结求扇形面积的方法。
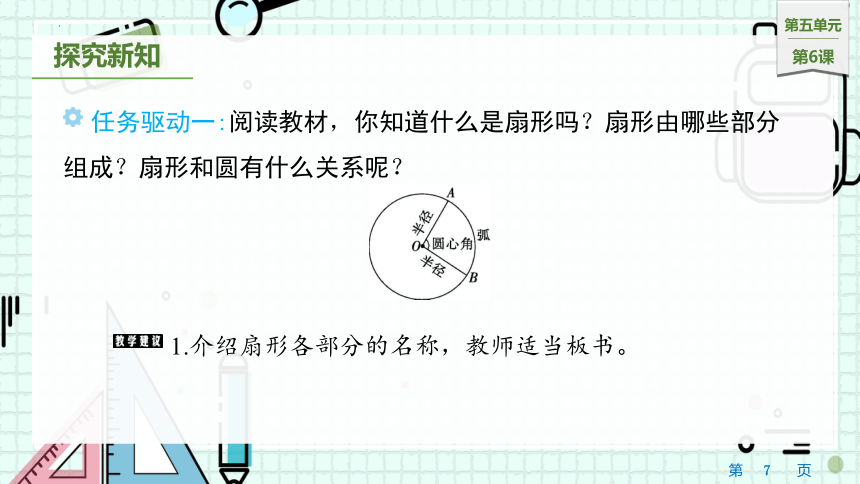
任务驱动一:阅读教材,你知道什么是扇形吗?扇形由哪些部分组成?扇形和圆有什么关系呢?
1.介绍扇形各部分的名称,教师适当板书。
如上图,圆上A、B两点之间的部分叫作弧,读作“弧AB”。一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。扇形是圆的一部分。
4.小结:像∠AOB这样,顶点在圆心的角叫作圆心角。
2.教师提问:从一点引出两条射线,组成的图形叫什么?(角)在扇形中,大家能找出角吗?(∠AOB)
3.让学生观察后说一说:∠AOB的顶点在圆的什么位置上?(圆心)两条边又分别是圆的什么?(半径)
任务驱动二:观察下图,这三个圆半径相等,三个扇形哪个比较大?哪个比较小?扇形的大小和什么有关呢?以半圆为弧的扇形的圆心角是多少度?以圆为弧的扇形呢?
1.三个扇形中最右边的扇形最大,最左边的扇形最小。以半圆为弧的扇形的圆心角是180°,以圆为弧的扇形的圆心角是90°。
2.用折扇演示扇形大小的变化情况。同一把扇子,张开程度的不同,扇面的大小就不同。
3.教师小结:在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
扇形
一、填空题。
1.以半圆为弧的扇形的圆心角是( 180 )度,以圆为弧的扇形的圆心角是( 90 )度。
2.顶点在( 圆心 )的角叫作圆心角。在同一个圆中,圆心角是50°的扇形面积比圆心角是55°的扇形面积( 小 )。
180
90
圆心
小
3.把直径为18厘米的圆等分成9个扇形,每个扇形的周长是( 24.28 )厘米。
24.28
二、画一个半径是1 cm的圆,再在圆中画一个圆心角是120°的扇形。
画图略。
三、求下列各扇形的面积。
1. 2. 3.
1.3.14×32÷(360÷60)=4.71(cm2)
2.3.14×22÷4=3.14(cm2)
3.3.14×(8÷2)2÷2=25.12(cm2)
四、把一个半径为6厘米的圆分成两部分,其中涂色部分是一个圆心角为120°的扇形。你能算出涂色部分的面积吗?
3.14×62×120÷360=37.68(平方厘米)
答:涂色部分的面积是37.68平方厘米。
五、一只挂钟的分针长20厘米(分针旋转点到分针针尖的长度),45分钟后,分针所扫过的钟面的面积是多大?
3.14×202×=942(平方厘米)
答:分针所扫过的钟面的面积是942平方厘米。
END
感谢观看 下节课再会
6 扇形
第五单元 圆
1.认识弧、圆心角以及它们间的对应关系,掌握扇形的基本特征,能准确判别扇形,知道圆心角及半径的大小决定扇形的大小。
2.在观察、比较、讨论、判断等活动中,初步经历认识扇形的过程,通过比一比、画一画等操作活动,提高动手操作、与人合作的能力。
3.在体会扇形和圆的密切联系中感受数学知识之间的内在联系。
温习旧知
一、求下图阴影部分的周长和面积。(单位:dm)
周长:3.14×10×2=62.8(dm)
面积:3.14×(10÷2)2÷2×4-10×10=57(dm2)
二、我国古代钱币形为外圆内方,寓意天圆地方。下图是清代的一枚铜钱及其示意图,这枚铜钱的面积是多少?
3÷2=1.5(cm) 3.14×1.52-0.82=6.425(cm2)
答:这枚铜钱的面积是6.425平方厘米。
知识链接
气象学家洛伦兹写了一篇论文,标题为《一只蝴蝶拍一下翅膀会不会在得克萨斯州引起龙卷风》,论述某系统如果初期条件差一点点,结果会很不稳定,他把这种现象称作“蝴蝶效应”。就像我们投掷骰子两次,无论如何刻意去投掷,投出的点数都不一定是相同的。
预习新知
一、课前自学扇形,完成温习旧知,初步认识扇形、圆心角、弧。
二、课堂中和同学合作交流什么是扇形,扇形的面积和什么有关,合作探究如何求扇形的面积。
三、课堂中和老师一起认识扇形、圆心角、弧,能正确辨认扇形和圆心角,总结求扇形面积的方法。
任务驱动一:阅读教材,你知道什么是扇形吗?扇形由哪些部分组成?扇形和圆有什么关系呢?
1.介绍扇形各部分的名称,教师适当板书。
如上图,圆上A、B两点之间的部分叫作弧,读作“弧AB”。一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。扇形是圆的一部分。
4.小结:像∠AOB这样,顶点在圆心的角叫作圆心角。
2.教师提问:从一点引出两条射线,组成的图形叫什么?(角)在扇形中,大家能找出角吗?(∠AOB)
3.让学生观察后说一说:∠AOB的顶点在圆的什么位置上?(圆心)两条边又分别是圆的什么?(半径)
任务驱动二:观察下图,这三个圆半径相等,三个扇形哪个比较大?哪个比较小?扇形的大小和什么有关呢?以半圆为弧的扇形的圆心角是多少度?以圆为弧的扇形呢?
1.三个扇形中最右边的扇形最大,最左边的扇形最小。以半圆为弧的扇形的圆心角是180°,以圆为弧的扇形的圆心角是90°。
2.用折扇演示扇形大小的变化情况。同一把扇子,张开程度的不同,扇面的大小就不同。
3.教师小结:在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
扇形
一、填空题。
1.以半圆为弧的扇形的圆心角是( 180 )度,以圆为弧的扇形的圆心角是( 90 )度。
2.顶点在( 圆心 )的角叫作圆心角。在同一个圆中,圆心角是50°的扇形面积比圆心角是55°的扇形面积( 小 )。
180
90
圆心
小
3.把直径为18厘米的圆等分成9个扇形,每个扇形的周长是( 24.28 )厘米。
24.28
二、画一个半径是1 cm的圆,再在圆中画一个圆心角是120°的扇形。
画图略。
三、求下列各扇形的面积。
1. 2. 3.
1.3.14×32÷(360÷60)=4.71(cm2)
2.3.14×22÷4=3.14(cm2)
3.3.14×(8÷2)2÷2=25.12(cm2)
四、把一个半径为6厘米的圆分成两部分,其中涂色部分是一个圆心角为120°的扇形。你能算出涂色部分的面积吗?
3.14×62×120÷360=37.68(平方厘米)
答:涂色部分的面积是37.68平方厘米。
五、一只挂钟的分针长20厘米(分针旋转点到分针针尖的长度),45分钟后,分针所扫过的钟面的面积是多大?
3.14×202×=942(平方厘米)
答:分针所扫过的钟面的面积是942平方厘米。
END
感谢观看 下节课再会
