河北省石家庄市裕华区2022-2023学年八年级上学期 期末考试数学试题(含图片答案)
文档属性
| 名称 | 河北省石家庄市裕华区2022-2023学年八年级上学期 期末考试数学试题(含图片答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 18:05:17 | ||
图片预览



文档简介
2022--2023 学年第一学期裕华区八年级期末考试
数学学科试卷
一、选择题(本大题有 16 个小题,每小题2分,共 32 分。在每小题给出的四个选项中,只有一项是 时间:90 分钟 满分:100 分
合题目要求的)
1.下列图标中,是轴对称图形的是( )
A B C D
2、若一= M (a≠b),则 M 可以是( )
A. B. C. D.
3.如图 ∠AOB=30°,点C 在射线 OB 上,若OC=6,则点C到OA 的距离等于( )
A.3 B. D .12
4、若 m= ,估计 m 的值所在的范围是( )
A.05.如图,在△ABC中,AB的垂直平分线分别交 AB、BC于点D、E,连接AE,若AE=2,
EC=1,则 BC 的长是( )
A.2 B.3 C.4 D.5
6.若关于 x 的方程有增根,则 m 的值是 ( )
A. -2 B.2 C.-3 D .3
7.用反证法证明命题·在△ABC 中,若∠B∠C,则 ABAC”,首先应假设( )
A. AB=AC B. ∠B=∠C C.AB≥AC D. ∠B≤∠C
8.如图,直线 MN 是四边形 AMBN 的对称轴,点 P是直线 MN 上的点,下判断错误的是( )
A. AM=BM B.∠MAP=∠MBP C.AP=BN D. ∠ANM=∠BNM
9.下列计算正确的是( )
B. C. D.
10.如图,CD⊥AB 于点 D,EF⊥AB 于点 F,CD=EF. 要根据“HL证明 Rt△ACD≌Rt△BEF,则还需要添加的条件是( )
A. ∠A=∠B B. ∠C=∠E C.AD=BF D. AC=BE
11.下列说法,其中错误的有( )
①81的平方根是 9 ② 是2的算术平方 ③-8的立方根为±2 ④ =a
A.1 个 B. 2 个 C.3个 D.4个
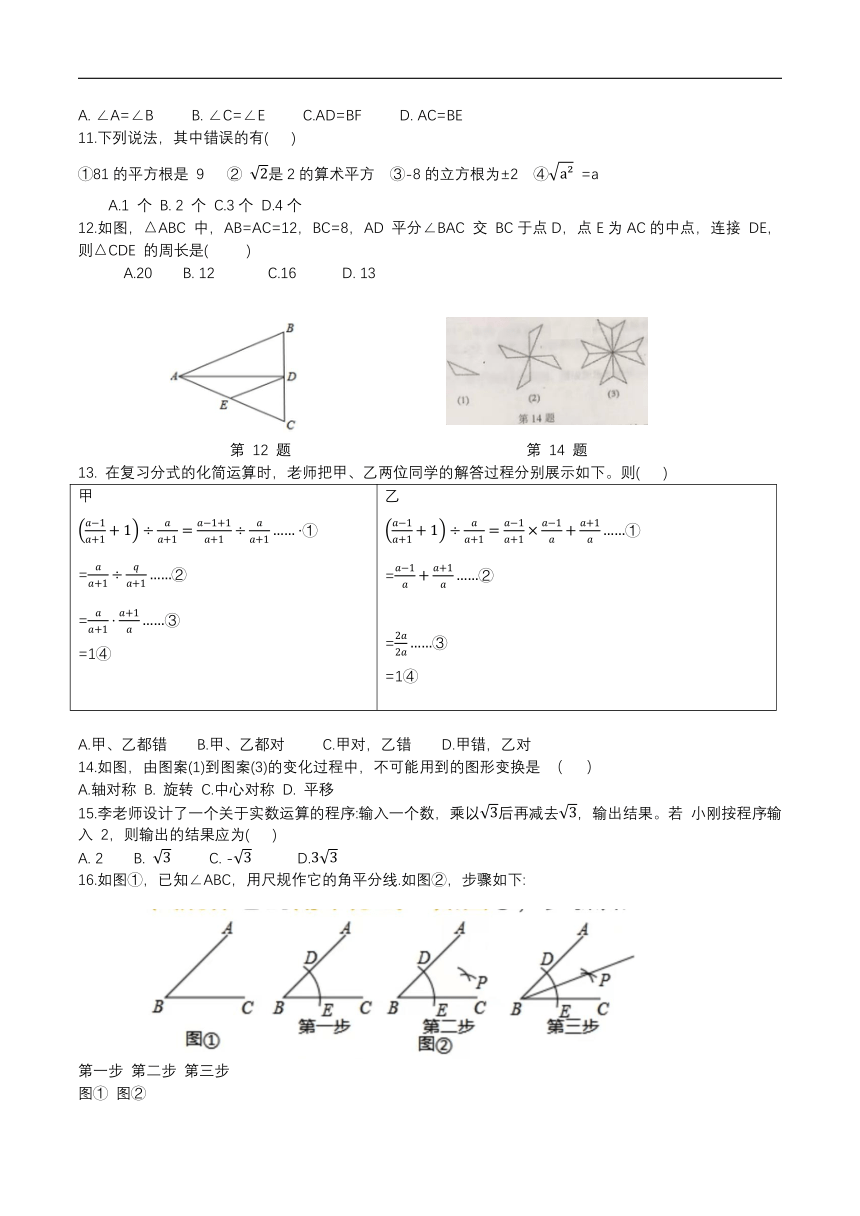
12.如图,△ABC 中,AB=AC=12,BC=8,AD 平分∠BAC 交 BC于点D,点E为AC的中点,连接 DE,则△CDE 的周长是( )
A.20 B. 12 C.16 D. 13
第 12 题 第 14 题
13. 在复习分式的化简运算时,老师把甲、乙两位同学的解答过程分别展示如下。则( )
甲 ① = = =1④ 乙 ① = = =1④
A.甲、乙都错 B.甲、乙都对 C.甲对,乙错 D.甲错,乙对
14.如图,由图案(1)到图案(3)的变化过程中,不可能用到的图形变换是 ( )
A.轴对称 B. 旋转 C.中心对称 D. 平移
15.李老师设计了一个关于实数运算的程序:输入一个数,乘以后再减去,输出结果。若 小刚按程序输入 2,则输出的结果应为( )
A. 2 B. C. - D.
16.如图①,已知∠ABC,用尺规作它的角平分线.如图②,步骤如下:
第一步 第二步 第三步
图① 图②
第一步:以B为圆心,以a为半径画弧,分别交射线 BA,BC 于点 D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC 内部交于点 P;
第三步:画射线 BP、射线 BP即为所求。则下列说法正确的是( )
A.a>0,b>DE 的长 B.a,b 均无限制 C.a 有最小限制,b 无限制 D、a≥0,b二、填空题(本大题有 4个小题,每小题 3分,共 12分)
17、把 2.45136 替确到十分位,得到近似数为_2.5. 25x1
18.如图,△ABC 是直角三角形,点C表示-2 ,且 AC=3,AB=1,若以点C 为圆心,CB 为半径画弧交数轴于点M,则点M表示的数为
19.若a=3-,b=,则a b (用< > =填空)
20、在等腰△ABC 中,AC 为腰,O 为 BC 中点,OD//AC 交AB 于点 D,∠ C=30°,则∠ ADO 的度数是
三、解答题(本大题有 7 个小题,共 56 分。解答应写出文字说明、证明过程或演算步骤)
21.(本题有 4 个小题,每题 3 分,共 12 分)
22.填空:(本小题满分 6 分) 二42
如图,点 F,C在线段 BE上,BF=CE,AB=DE,AB//DE.求证:AC=DE
证明::BF=CE,
∴BF+FC=FC+ ,即BC=
∵AB // DE,
∴∠B=
在△ABC 与△DEF 中, Bv/ C
BC=
∠B =
;AB= DE.
∴△ABC ≌ ΔDEF ( )
∴AC=DF(全等三角形的对应边相等).
23.(本小题满分 6 分)
先化简,再求值:
24.(本小题满分 8 分) C
如图,把一块直角三角形 ABC(其中∠ACB=90°)土地划出一个△ADC 后,测得 CD=3 米,AD =4 米, BC=12 米,AB=13 米.
根据条件,求 AC 的长度:
(2)判断△ACD 的形状,并说明理由.
(3)图中阴影部分土地的面积是 平方米.
25.(本小题满分 8 分)
某市在招商期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来400 平方米的正方形场地改建成 315 平方米的长方形场地,且其长、宽的比为 5:3.
(1)求原来正方形场地的周长;
(2)如果把原来正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用 试利用所学知识说明理由.
26.(本小题满分 8分)
用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运 20袋大米,若A型机器人运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋米
(1)设A型机器人每小时搬运x袋大米,则B型机器人每小时搬运 袋大米.根据题意,
则 A型机器人搬运700袋大米所用的时间是 小时,
B型机器人搬运 500袋大米所用的时间是. 小时.(用含x的代数式填空)
根据题意,列出分式方程解决问题.
27.(本小题满分 8分)
如图,己知等边△ABC 的边长为 6cm,现有两点 M、N 分别从点 A、点 B 同时出发,沿三角形的边运动,运动时间为t s,已知点 M的速度为 1cm/s,点 N的速度为2cm/s.当点 N 第一次到达 B 点时,M、N 同时停止运动.
(1) 当点 N 第一次到达 B 点时,点M的位置在
当 M、N运动 秒时,点N追上点M;
2)当点 M、N 在 BC边上运动时,能否得到以MN为底边的等腰三角形△AMN
如存在,请求出此时 M、N 运动的时间.
3)当△AMN 为直角三角形时,运动时间t的值是
参考答案
数学学科试卷
一、选择题(本大题有 16 个小题,每小题2分,共 32 分。在每小题给出的四个选项中,只有一项是 时间:90 分钟 满分:100 分
合题目要求的)
1.下列图标中,是轴对称图形的是( )
A B C D
2、若一= M (a≠b),则 M 可以是( )
A. B. C. D.
3.如图 ∠AOB=30°,点C 在射线 OB 上,若OC=6,则点C到OA 的距离等于( )
A.3 B. D .12
4、若 m= ,估计 m 的值所在的范围是( )
A.0
EC=1,则 BC 的长是( )
A.2 B.3 C.4 D.5
6.若关于 x 的方程有增根,则 m 的值是 ( )
A. -2 B.2 C.-3 D .3
7.用反证法证明命题·在△ABC 中,若∠B∠C,则 ABAC”,首先应假设( )
A. AB=AC B. ∠B=∠C C.AB≥AC D. ∠B≤∠C
8.如图,直线 MN 是四边形 AMBN 的对称轴,点 P是直线 MN 上的点,下判断错误的是( )
A. AM=BM B.∠MAP=∠MBP C.AP=BN D. ∠ANM=∠BNM
9.下列计算正确的是( )
B. C. D.
10.如图,CD⊥AB 于点 D,EF⊥AB 于点 F,CD=EF. 要根据“HL证明 Rt△ACD≌Rt△BEF,则还需要添加的条件是( )
A. ∠A=∠B B. ∠C=∠E C.AD=BF D. AC=BE
11.下列说法,其中错误的有( )
①81的平方根是 9 ② 是2的算术平方 ③-8的立方根为±2 ④ =a
A.1 个 B. 2 个 C.3个 D.4个
12.如图,△ABC 中,AB=AC=12,BC=8,AD 平分∠BAC 交 BC于点D,点E为AC的中点,连接 DE,则△CDE 的周长是( )
A.20 B. 12 C.16 D. 13
第 12 题 第 14 题
13. 在复习分式的化简运算时,老师把甲、乙两位同学的解答过程分别展示如下。则( )
甲 ① = = =1④ 乙 ① = = =1④
A.甲、乙都错 B.甲、乙都对 C.甲对,乙错 D.甲错,乙对
14.如图,由图案(1)到图案(3)的变化过程中,不可能用到的图形变换是 ( )
A.轴对称 B. 旋转 C.中心对称 D. 平移
15.李老师设计了一个关于实数运算的程序:输入一个数,乘以后再减去,输出结果。若 小刚按程序输入 2,则输出的结果应为( )
A. 2 B. C. - D.
16.如图①,已知∠ABC,用尺规作它的角平分线.如图②,步骤如下:
第一步 第二步 第三步
图① 图②
第一步:以B为圆心,以a为半径画弧,分别交射线 BA,BC 于点 D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC 内部交于点 P;
第三步:画射线 BP、射线 BP即为所求。则下列说法正确的是( )
A.a>0,b>DE 的长 B.a,b 均无限制 C.a 有最小限制,b 无限制 D、a≥0,b
17、把 2.45136 替确到十分位,得到近似数为_2.5. 25x1
18.如图,△ABC 是直角三角形,点C表示-2 ,且 AC=3,AB=1,若以点C 为圆心,CB 为半径画弧交数轴于点M,则点M表示的数为
19.若a=3-,b=,则a b (用< > =填空)
20、在等腰△ABC 中,AC 为腰,O 为 BC 中点,OD//AC 交AB 于点 D,∠ C=30°,则∠ ADO 的度数是
三、解答题(本大题有 7 个小题,共 56 分。解答应写出文字说明、证明过程或演算步骤)
21.(本题有 4 个小题,每题 3 分,共 12 分)
22.填空:(本小题满分 6 分) 二42
如图,点 F,C在线段 BE上,BF=CE,AB=DE,AB//DE.求证:AC=DE
证明::BF=CE,
∴BF+FC=FC+ ,即BC=
∵AB // DE,
∴∠B=
在△ABC 与△DEF 中, Bv/ C
BC=
∠B =
;AB= DE.
∴△ABC ≌ ΔDEF ( )
∴AC=DF(全等三角形的对应边相等).
23.(本小题满分 6 分)
先化简,再求值:
24.(本小题满分 8 分) C
如图,把一块直角三角形 ABC(其中∠ACB=90°)土地划出一个△ADC 后,测得 CD=3 米,AD =4 米, BC=12 米,AB=13 米.
根据条件,求 AC 的长度:
(2)判断△ACD 的形状,并说明理由.
(3)图中阴影部分土地的面积是 平方米.
25.(本小题满分 8 分)
某市在招商期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来400 平方米的正方形场地改建成 315 平方米的长方形场地,且其长、宽的比为 5:3.
(1)求原来正方形场地的周长;
(2)如果把原来正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用 试利用所学知识说明理由.
26.(本小题满分 8分)
用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运 20袋大米,若A型机器人运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋米
(1)设A型机器人每小时搬运x袋大米,则B型机器人每小时搬运 袋大米.根据题意,
则 A型机器人搬运700袋大米所用的时间是 小时,
B型机器人搬运 500袋大米所用的时间是. 小时.(用含x的代数式填空)
根据题意,列出分式方程解决问题.
27.(本小题满分 8分)
如图,己知等边△ABC 的边长为 6cm,现有两点 M、N 分别从点 A、点 B 同时出发,沿三角形的边运动,运动时间为t s,已知点 M的速度为 1cm/s,点 N的速度为2cm/s.当点 N 第一次到达 B 点时,M、N 同时停止运动.
(1) 当点 N 第一次到达 B 点时,点M的位置在
当 M、N运动 秒时,点N追上点M;
2)当点 M、N 在 BC边上运动时,能否得到以MN为底边的等腰三角形△AMN
如存在,请求出此时 M、N 运动的时间.
3)当△AMN 为直角三角形时,运动时间t的值是
参考答案
同课章节目录
