2022-2023学年冀教版九年级数学下册29.4切线长定理课后综合练习(无答案)
文档属性
| 名称 | 2022-2023学年冀教版九年级数学下册29.4切线长定理课后综合练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 379.4KB | ||
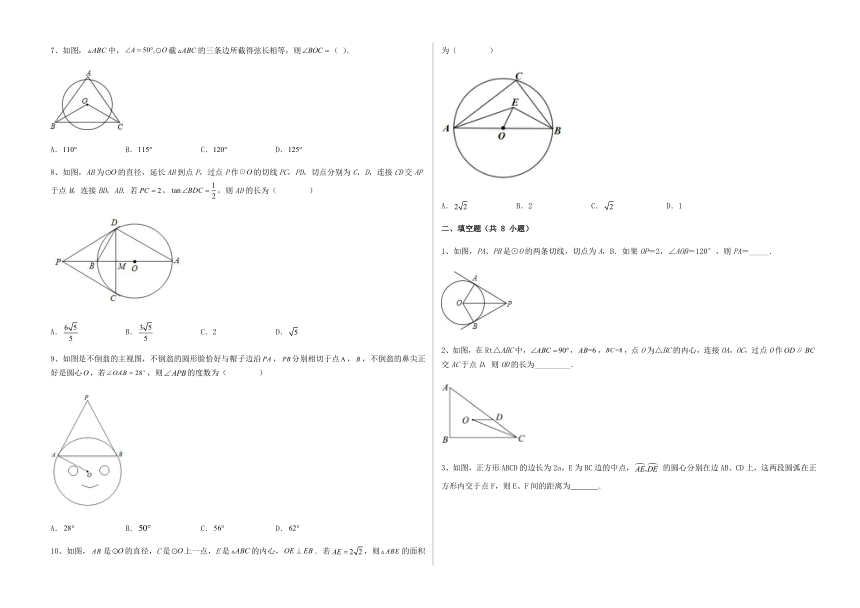
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-18 17:48:32 | ||
图片预览

文档简介
29.4切线长定理课后综合练习
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,点A是⊙O外一点,过点A作⊙O的切线AB、AC,切点分别为B、C两点,连结AC并延长交BO的延长线于点D.若AB=3,BD=4,则⊙O的半径为( )
A. B. C. D.
2、如图,已知切于点,点在上,且,连结并延长交于点,的半径为2,设,
①当m=时,是等腰直角三角形;
②若,则;
③当时,与相切.以上列选项正确的有( )
A.② B.③ C.②③ D.①③
3、如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D.若⊙O的半径为,AB=4,则BC的长是( )
A.2 B.3 C.4 D.3
4、直角三角形的外接圆半径为3,内切圆半径为1,则该直角三角形的周长是( )
A.12 B.14 C.16 D.18
5、如图,,是⊙O的切线,切点为、,点为优弧上一点,且,若.则等于( )
A.100° B.15° C.20° D.25°
6、如图,在Rt△ABC中,∠ACB=90°,CB=7,AC=9,以C为圆心、3为半径作⊙C,P为⊙C上一动点,连接AP、BP,则AP+BP的最小值为( )
A.7 B.5 C. D.
7、如图,中,截的三条边所截得弦长相等,则( ).
A. B. C. D.
8、如图,AB为的直径,延长AB到点P,过点P作的切线PC,PD,切点分别为C,D,连接CD交AP于点M,连接BD,AD.若,,则AD的长为( )
A. B. C.2 D.
9、如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿,分别相切于点,,不倒翁的鼻尖正好是圆心,若,则的度数为( )
A. B. C. D.
10、如图,是的直径,C是上一点,E是的内心,.若,则的面积为( )
A. B.2 C. D.1
二、填空题(共 8 小题)
1、如图,PA、PB是⊙O的两条切线,切点为A,B.如果OP=2,∠AOB=120°,则PA=_____.
2、如图,在Rt△ABC中,,,,点O为△BC的内心,连接OA,OC,过点O作交AC于点D,则OD的长为_________.
3、如图,正方形ABCD的边长为2a,E为BC边的中点, 的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为 .
4、如图,⊙O是△ABC的内切圆,与AB,BC,CA的切点分别为D,E,F,若∠BDE+∠CFE=110°,则∠A的度数是________.
5、在△ABC中,AB=6,AC=8,高AD=4.8,设能完全覆盖△ABC的圆的半径为r,则r的最小值为______.
6、《九章算术》是我国古代数学名著,也是古代东方数学的代表作之一.书中记载了一个问题:“今有勾五步,股十二步,问勾中容圆半径几何?”译文:“如图,今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的圆(内切圆)的半径是多少步?”根据题意,该直角三角形内切圆的半径为____步.
7、如图,PA,PB是的切线,切点分别为A,B,连接OB,AB.如果,那么∠P的度数为______.
8、如图,内接于,,于点,.若的半径为5,则的长为 __.
三、解答题(共 6 小题)
1、如图,为半圆的圆心,、为半圆上的两点,连接、、,,连接并延长,与的延长线相交于点.
(1)求证:;
(2)若,半径,求的长
2、如图,BE为⊙O的直径,点A和点D是⊙O上的两点,连接AE,AD,DE,过点A作射线交BE的延长线于点C,使∠EAC=∠EDA.
(1)求证:AC是⊙O的切线;
(2)若AD⊥BC于点F,DE=4,OF=2,求图中阴影部分的面积.
3、已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
4、定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形中,,,过点作垂线交的延长线于点,且,证明:四边形是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为的垂等四边形内接于⊙O中,.求⊙O的半径.
5、如图,已知,.
(1)在图中,用尺规作出的内切圆,并标出与边,,的切点(保留痕迹,不必写作法);
(2)连接,,求的度数.
6、已知为的直径,,C为上一点,连接.
(1)如图①,若C为的中点,求的大小和的长;
(2)如图②,若为的半径,且,垂足为E,过点D作的切线,与的延长线相交于点F,求的长.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,点A是⊙O外一点,过点A作⊙O的切线AB、AC,切点分别为B、C两点,连结AC并延长交BO的延长线于点D.若AB=3,BD=4,则⊙O的半径为( )
A. B. C. D.
2、如图,已知切于点,点在上,且,连结并延长交于点,的半径为2,设,
①当m=时,是等腰直角三角形;
②若,则;
③当时,与相切.以上列选项正确的有( )
A.② B.③ C.②③ D.①③
3、如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D.若⊙O的半径为,AB=4,则BC的长是( )
A.2 B.3 C.4 D.3
4、直角三角形的外接圆半径为3,内切圆半径为1,则该直角三角形的周长是( )
A.12 B.14 C.16 D.18
5、如图,,是⊙O的切线,切点为、,点为优弧上一点,且,若.则等于( )
A.100° B.15° C.20° D.25°
6、如图,在Rt△ABC中,∠ACB=90°,CB=7,AC=9,以C为圆心、3为半径作⊙C,P为⊙C上一动点,连接AP、BP,则AP+BP的最小值为( )
A.7 B.5 C. D.
7、如图,中,截的三条边所截得弦长相等,则( ).
A. B. C. D.
8、如图,AB为的直径,延长AB到点P,过点P作的切线PC,PD,切点分别为C,D,连接CD交AP于点M,连接BD,AD.若,,则AD的长为( )
A. B. C.2 D.
9、如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿,分别相切于点,,不倒翁的鼻尖正好是圆心,若,则的度数为( )
A. B. C. D.
10、如图,是的直径,C是上一点,E是的内心,.若,则的面积为( )
A. B.2 C. D.1
二、填空题(共 8 小题)
1、如图,PA、PB是⊙O的两条切线,切点为A,B.如果OP=2,∠AOB=120°,则PA=_____.
2、如图,在Rt△ABC中,,,,点O为△BC的内心,连接OA,OC,过点O作交AC于点D,则OD的长为_________.
3、如图,正方形ABCD的边长为2a,E为BC边的中点, 的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为 .
4、如图,⊙O是△ABC的内切圆,与AB,BC,CA的切点分别为D,E,F,若∠BDE+∠CFE=110°,则∠A的度数是________.
5、在△ABC中,AB=6,AC=8,高AD=4.8,设能完全覆盖△ABC的圆的半径为r,则r的最小值为______.
6、《九章算术》是我国古代数学名著,也是古代东方数学的代表作之一.书中记载了一个问题:“今有勾五步,股十二步,问勾中容圆半径几何?”译文:“如图,今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的圆(内切圆)的半径是多少步?”根据题意,该直角三角形内切圆的半径为____步.
7、如图,PA,PB是的切线,切点分别为A,B,连接OB,AB.如果,那么∠P的度数为______.
8、如图,内接于,,于点,.若的半径为5,则的长为 __.
三、解答题(共 6 小题)
1、如图,为半圆的圆心,、为半圆上的两点,连接、、,,连接并延长,与的延长线相交于点.
(1)求证:;
(2)若,半径,求的长
2、如图,BE为⊙O的直径,点A和点D是⊙O上的两点,连接AE,AD,DE,过点A作射线交BE的延长线于点C,使∠EAC=∠EDA.
(1)求证:AC是⊙O的切线;
(2)若AD⊥BC于点F,DE=4,OF=2,求图中阴影部分的面积.
3、已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
4、定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形中,,,过点作垂线交的延长线于点,且,证明:四边形是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为的垂等四边形内接于⊙O中,.求⊙O的半径.
5、如图,已知,.
(1)在图中,用尺规作出的内切圆,并标出与边,,的切点(保留痕迹,不必写作法);
(2)连接,,求的度数.
6、已知为的直径,,C为上一点,连接.
(1)如图①,若C为的中点,求的大小和的长;
(2)如图②,若为的半径,且,垂足为E,过点D作的切线,与的延长线相交于点F,求的长.
