第一单元《简易方程》(周测)苏教版五年级下册数学(带答案)
文档属性
| 名称 | 第一单元《简易方程》(周测)苏教版五年级下册数学(带答案) |  | |
| 格式 | docx | ||
| 文件大小 | 187.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 15:39:48 | ||
图片预览




文档简介
苏教版数学五下第一单元《简易方程》周测(一)
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、选择题(共10分)
1.(本题1分)小明做了x个灯笼,小军做了24个灯笼。小军送给小明4个后,两人的灯笼数就一样多了。下列方程正确的是( )。
A. B. C. D.
2.(本题1分)与方程x+0.8x=36有相同解的是( )。
A.1.68+x=3.98 B.x÷35=6.8 C.12x÷16=4.32 D.43-x=23
3.(本题1分)乐乐35张卡片,笑笑y张卡片,乐乐给笑笑4张后,两人卡片张数相同,下列方程正确的是( )。
A.35-y=4 B.y-8=35
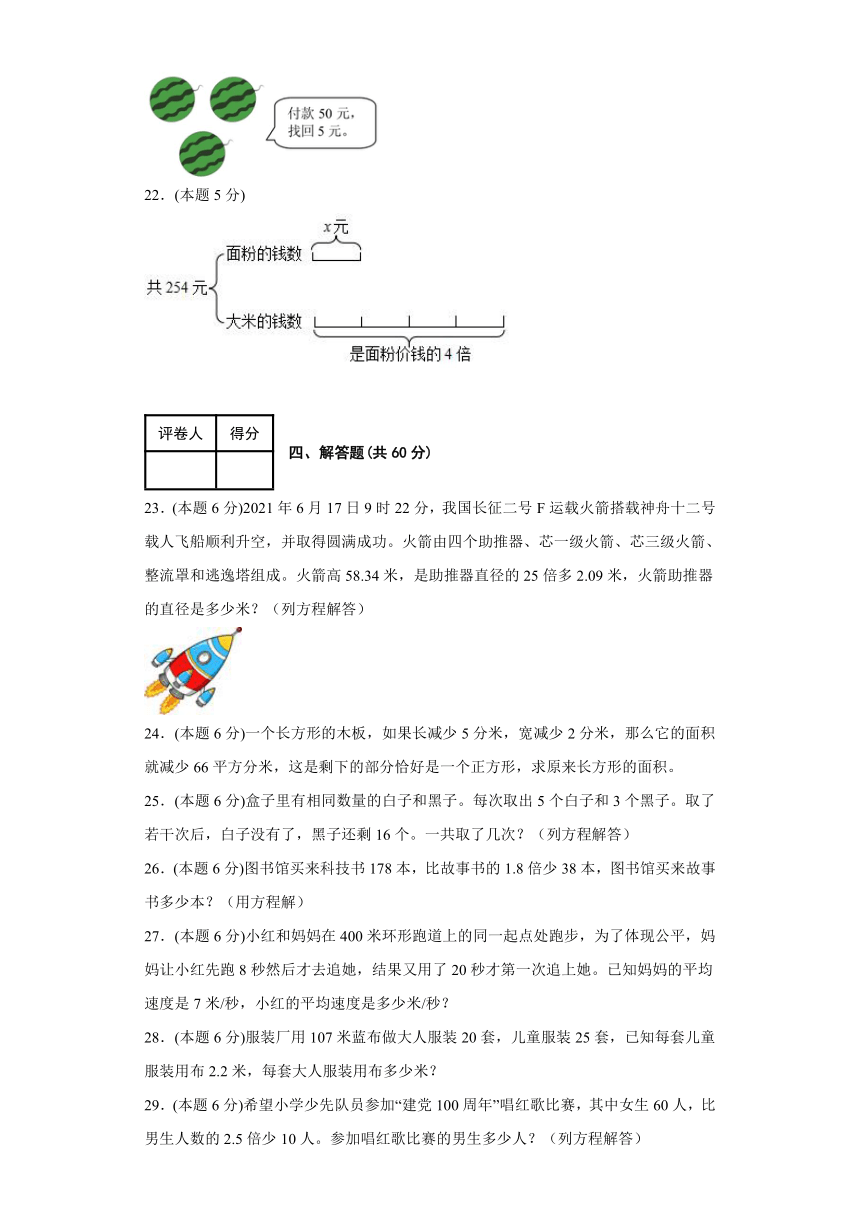
C.y+4=35 D.y+4=35-4
4.(本题1分)下列式子中方程有( )个。
① ② ③ ④ ⑤
A.1 B.2 C.3 D.4
5.(本题1分)如果4x+1.4=4.2,那么18-10x=( )。
A.14 B.11 C.4 D.25
6.(本题1分)男生有x人,男生人数比女生人数的3倍多1人,女生有( )人。
A.3x+1 B.3x-1 C.(x-1)÷3 D.(x+1)÷3
7.(本题1分)a+7=b+4 ,那么a( )b。
A.大于 B.小于 C.等于 D.无法确定
8.(本题1分)在一个停车场,现停相同数量的四轮车和两轮车,两种车共有84个轮子,那么停车场两轮车有( )辆。
A.18 B.14 C.12 D.10
9.(本题1分)五年级两个班同学一共积肥1420千克,甲班有50人,平均每人积肥14千克,乙班有48人,平均每人积肥多少千克?
解:设乙班平均每人积肥x千克
列出方程正确的是( )
A.48x+14×50=1420 B.48x+14=1420 C.(x+14)×50=1420 D.x+14×50=1420
10.(本题1分)一辆大汽车每天运货10.5吨,是小汽车运货量的3.5倍,小汽车的运货量是( )
A.14吨 B.7吨 C.3吨 D.10吨
评卷人得分
二、填空题(共20分)
11.(本题2分)当X=( )时,7X与56相等,当X=( )时,7X-12与3X相等。
12.(本题2分)用方程表示数量关系。
一条裤子y元,一件上衣的价格是一条裤子的2.2倍,一件上衣比一条裤子贵60元( )。
13.(本题2分)若,则( )。
14.(本题2分)如果3个连续自然数的和是99,那么这3个数中最小的是( )。
15.(本题2分)在( )里填上“”“”或“”。
当时,( )30;( )32;
当时,( )0.12;( )0.2。
16.(本题2分)如果,那么( )。
17.(本题2分)在5+x>9,y-16=54,20+30=50中等式是( );方程是( )。
18.(本题2分)根据“一头牛重510千克,大约是一只羊重量的12倍”可以得到数量间的相等关系式是:( )的体重×12=( )的体重。
19.(本题2分)黄花有n朵,红花比黄花少8朵,红花有( )朵;如果黄花的朵数是20朵,红花有( )朵。
20.(本题2分)吴伟买了1本练习本和3支铅笔,张兰买了8支同样的铅笔,两人用去的钱同样多。1本练习本的价钱=1支铅笔的价钱×( )。
评卷人得分
三、看图列方程,并解答(共10分)
21.(本题5分)
22.(本题5分)
评卷人得分
四、解答题(共60分)
23.(本题6分)2021年6月17日9时22分,我国长征二号F运载火箭搭载神舟十二号载人飞船顺利升空,并取得圆满成功。火箭由四个助推器、芯一级火箭、芯三级火箭、整流罩和逃逸塔组成。火箭高58.34米,是助推器直径的25倍多2.09米,火箭助推器的直径是多少米?(列方程解答)
24.(本题6分)一个长方形的木板,如果长减少5分米,宽减少2分米,那么它的面积就减少66平方分米,这是剩下的部分恰好是一个正方形,求原来长方形的面积。
25.(本题6分)盒子里有相同数量的白子和黑子。每次取出5个白子和3个黑子。取了若干次后,白子没有了,黑子还剩16个。一共取了几次?(列方程解答)
26.(本题6分)图书馆买来科技书178本,比故事书的1.8倍少38本,图书馆买来故事书多少本?(用方程解)
27.(本题6分)小红和妈妈在400米环形跑道上的同一起点处跑步,为了体现公平,妈妈让小红先跑8秒然后才去追她,结果又用了20秒才第一次追上她。已知妈妈的平均速度是7米/秒,小红的平均速度是多少米/秒?
28.(本题6分)服装厂用107米蓝布做大人服装20套,儿童服装25套,已知每套儿童服装用布2.2米,每套大人服装用布多少米?
29.(本题6分)希望小学少先队员参加“建党100周年”唱红歌比赛,其中女生60人,比男生人数的2.5倍少10人。参加唱红歌比赛的男生多少人?(列方程解答)
30.(本题6分)一个梯形的面积3.6平方厘米,上底长0.5厘米,高3厘米,下底长多少厘米?(列方程解答)
31.(本题6分)小明和小芳是集邮爱好者,小明的邮票数量是小芳的5倍,如果小明给小芳38张,他们的邮票数量正好相等,小明和小芳原来各有多少张邮票?(用方程解)
32.(本题6分)甲乙两个工程队合修一段720米的公路,同时各从一端开始修,经过10天修完。乙队每天修24米,甲队每天修多少米?(列方程解答)
参考答案:
1.D
【分析】根据题意,小军的灯笼数量-4=小明的灯笼数量+4,据此列出方程。
【详解】根据题中的数量关系,应列方程为:或x+4+4=24。
故答案为:D
【点睛】找出题目中的等量关系式是列方程解应用题的关键。
2.D
【分析】解出方程方程x+0.8x=36的解,然后带入各选项,看等号的两边是否相等,以此判断。
【详解】x+0.8x=36
解:1.8x=36
x=20
A.1.68+20=21.68≠3.98
B.20÷35≈0.57≠6.8
C.12×20÷16
=240÷16
=15
15≠4.32
D.43-20=23
故答案为:D
【点睛】此题主要考查学生对检验方程解的掌握与应用。
3.D
【分析】乐乐给笑笑4张后,乐乐还有35-4张卡片,笑笑这时有y+4张卡片,由题意知:y+4=35-4。据此解答。
【详解】由分析知:
y+4=35-4
故答案为:D
【点睛】找出乐乐给笑笑4张后,乐乐现在有的卡片和笑笑现在有的卡片之间的等量关系是解答本题的关键。
4.C
【分析】根据方程的意义:含有未知数的等式,叫做方程;据此解答。
【详解】①55÷5=11,是等式,不含有未知数,不是方程;
②x+5<14,含有未知数,但不是等式,不是方程;
③8+a=10,既含有未知数,又是等式,是方程;
④5+36=x+35,既含有未知数,又是等式,是方程;
⑤x=5,既含有未知数,又是等式,是方程。
③、④、⑤有3个式子是方程。
故答案选:C
【点睛】本题考查方程的意义,根据方程的意义解答问题。
5.B
【分析】根据等式的性质,求出x的值,再代入18-10x求值即可。
【详解】4x+1.4=4.2
解:4x=4.2-1.4
x=2.8÷4
x=0.7
18-10x =18-10×0.7
=18-7
=11
故答案为:B
【点睛】本题主要考查根据等式的性质解方程。
6.C
【分析】根据题意女生人数的3倍加上1就是男生人数,所以女生人数就是男生人数减去1,然后再除以3,据此解答即可。
【详解】男生有x人,男生人数比女生人数的3倍多1人,女生有(x-1)÷3人。
故答案为:C
【点睛】本题重点考查了用字母表示数以及数量之间的关系。
7.B
【分析】等式的性质,等式两边同时加上或减去同一个数,等式仍然成立,再比较a与b的大小。
【详解】a+7=b+4,根据等式的性质1可得:
a+7-4=b+4-4
a+3=b
所以a<b。
故答案为:B
8.B
【分析】设两轮车有x辆,则四轮车也有x辆,两轮车的轮子个数为2x,四轮车的轮子个数为4x,相加等于84,据此列方程解答即可。
【详解】解:设两轮车有x辆,则四轮车也有x辆。
2x+4x=84
6x=84
x=14
故选择:B。
【点睛】此题考查了用方程解决实际问题,找出等量关系,分别表示出两种车轮子个数是解题关键。
9.A
【分析】题意可知,“两个班一共积肥1420千克”是本题的关键句。数量之间存在以下相等关系:乙班平均每人积肥数量×人数+甲班平均每人积肥数量×人数=两个班一共积肥数量。
【详解】由分析可知列方程如下:48x+14×50=1420
故选择:A
【点睛】此题考查列方程解决实际问题,找出等量关系,分别求出两个班施肥质量是解题关键。
10.C
【分析】已知大货车每天运货10.5吨,是小汽车运货量的3.5倍,那么大货车运的多,小汽车运的少,设小汽车运货量为x吨,大货车运的量是小汽车的3.5倍,3.5x=等于大货车运的量。
【详解】解:设小汽车的运货量是x吨,根据题意列方程:
3.5x=10.5
x=10.5÷3.5
x=3
故答案为:C。
【点睛】本题考查方程的意义,根据题意找出等量关系,列方程,解方程。
11. 8 3
【分析】要求X的值,即是求7X=56与7X-12=3X两个方程的解,利用等式性质解方程即可。
【详解】根据分析可知:
7X=56
解:7X÷7=56÷7
X=8
7X-12=3X
解:7X-12+12=3X+12
7X=3X+12
7X-3X=3X+12-3X
4X=12
4X÷4=12÷4
X=3
所以当X=8时,7X与56相等,当X=3时,7X-12与3X相等。
【点睛】本题考查利用等式性质解方程,关键是建立方程。
12.2.2y-y=60
【分析】一条裤子y元,一件上衣的价钱是一条裤子的2.2倍,一件上衣的价格是2.2y元,一件上衣比一条裤子贵60元,用上衣的价格-裤子的价格=60元,列方程:2.2y-y=60,据此解答。
【详解】解:设一条裤子y元。
2.2y-y=60
1.2y=60
y=60÷1.2
y=50
【点睛】本题考查方程的应用,根据上衣的价钱与裤子的价钱关系,列方程。
13.60
【分析】根据等式的性质1,方程的两边同时加上8,求出方程x-8=7的解,再把方程的解带入4x,即可解答。
【详解】x-8=7
解:x-8+=7+8
x=15
4x=4×15=60
【点睛】本题考查解方程,根据等式的性质1,解方程,求出方程的解,进而求出4x的值。
14.32
【分析】设中间的自然数为x,找到关系式第一个自然数+中间的自然数+第三个自然数=99,列方程解答。
【详解】解:设中间的自然数为x。
x-1+x+x+1=99
3x=99
x=33
最小的数:33-1=32
【点睛】分析题意,找到合适的量设为未知数并列出等量关系式是列方程解题的重要步骤。
15. > > = <
【分析】根据题意,把x=12,带入式子x+19,计算出结果再和30比较大小;把x=12,带入式子60-x,求出结果再和32比较大小;
把x=0.2,带入式子0.6x,求出结果,再和0.12比较大小;把x=0.2,代入式子x÷0.2,求出结果,再和0.2比较大小;即可解答。
【详解】当x=12时
12+19=31;因为31>30,所以x+19>30
当x=12时
60-12=48,因为48>32,所以60-x>32
当x=0.2时
0.6×0.2=0.12,因为0.12=0.12,所以0.6x=0.12
当x=0.2时
0.2÷2=0.1,因为0.1<0.2,所以x÷0.2<0.2
【点睛】本题考查含有字母式子的化简与求值,以及两位数比较大小,小数比较大小。
16.56
【分析】先求得方程的解,再将解代入中,据此解答。
【详解】
解:
将代入中,
=54+2=56
【点睛】求得方程的解,是解答此题的关键。
17. y-16=54;20+30=50 y-16=54
【分析】根据方程和等式的意义:等式是指用等号连接的式子;方程是指含有未知数的等式;所有的方程都是等式,但等式不一定是方程;据此解答。
【详解】在5+x>9,y-16=54,20+30=50中等式是y-16=54;20+30=50;方程是y-16=54。
【点睛】本题考查等式和方程的意义,方程是等式,但等式不一定是方程。
18. 一只羊 一头牛
【分析】根据题意可知,一头牛的重量是一只羊重量的12倍。
【详解】根据分析可知,一只羊的体重×12=一头牛的体重。
【点睛】此题主要考查等式的认识及列等量关系式。
19. n-8 12
【分析】根据题意,黄花有n朵,红花比黄花少8朵,用黄花的朵数-8=红花的朵数;即n-8=红花朵数;如果黄花的朵数20朵,带入n-8式子,即可求出红花的朵数,据此解答。
【详解】红花有:n-8(朵)
黄花的朵数20朵,黄花有:20-8=12(朵)
【点睛】本题考查用字母表示数,以及含有字母的式子化简与求值。
20.5
【分析】根据题意可知,因为1本练习本的价钱+3支铅笔的价钱=8支铅笔的价钱,所以8支铅笔的价钱-3支铅笔的价钱=5支铅笔的价钱=1个练习本的价钱。
【详解】根据分析可知,1本练习本的价钱=5支铅笔的价钱=1支铅笔的价钱×5。
【点睛】此题主要考查学生对等量代换的应用。
21.3x=50-5
x=15
【分析】由于50元买了3个西瓜,还找回5元,那么相当于3个西瓜的价钱=50-5,据此即可列方程,再根据等式的性质解方程即可。
【详解】3x=50-5
解:3x=45
x=45÷3
x=15
每个西瓜15元。
22.50.8元
【分析】设面粉的钱数是x元,已知大米是面粉价钱的4倍,则面粉的价钱是4x元,由图可知:面粉的钱数加上大米的钱数共254元,据此列出方程并求解即可。
【详解】解:设面粉的钱数是x元,根据题意列方程如下:
x+4x=254
5x=254
x=50.8
面粉的钱数是50.8元。
23.2.25米
【分析】根据“火箭高58.34米,是助推器直径的25倍多2.09米”这一信息,可分析出此题等量关系为:助推器的直径×25+2.09=火箭的高度,设火箭助推器的直径是x米,列出方程并依据等式的性质1和2解答即可。
【详解】解:设火箭助推器的直径是x米。
25x+2.09=58.34
25x+2.09-2.09=58.34-2.09
25x=56.25
25x÷25=56.25÷25
x=2.25
答:火箭助推器的直径是2.25米。
【点睛】此题重点考查列方程解决实际问题的能力,关键是要找准等量关系式。
24.130平方分米
【分析】如图所示,设正方形的边长为a厘米,则减少的面积为长和宽分别是(a+5)分米、2分米与a分米、5分米的两个长方形的面积和,据此就可列等式求出a的值,从而求出原来长方形的面积。
【详解】解:设正方形的边长为a分米。
则(a+5)×2+5a=66
2a+10+5a=66
7a=66-10
7a=56
a=56÷7
a=8
原长方形的面积:(8+5)×(8+2)
=13×10
=130(平方分米)
答:原来长方形的面积是130平方分米。
【点睛】解决此题的关键是先求出正方形的边长,进而求得原长方形的面积。
25.8次
【分析】设一共取了x次,白子全部被取出,可知白子一共5x个,黑子数量是(3x+16)个,列出等量关系式,解方程即可。
【详解】解:设一共取了x次。
5x=3x+16
2x=16
x=8
答:一共取了8次。
【点睛】根据白子和黑子总数量相等列出等量关系是解题的关键。
26.120本
【分析】根据题意,设图书馆买来故事书x本,科技书比故事书的1.8倍少38本,就是故事书×1.8再减去38本等于科技书的本数,列方程:1.8x-38=178,解方程,即可解答。
【详解】解:设图书馆买来故事书x本。
1.8x-38=178
1.8x=178+38
1.8x=216
x=216÷1.8
x=120
答:图书馆买来故事书120本。
【点睛】根据方程的实际应用,利用买来的故事书与科技书之间的关系,设出未知数,列方程,解方程。
27.5米/秒
【分析】根据题意,妈妈跑了20秒,妈妈的平均速度是7米/秒,用7×20,求出妈妈跑的路程;小红跑了8+20秒,小红跑的路程和妈妈跑的路程一样长,设:小红的平均速度是x米/秒;小红跑的路程是(20+8)×x米;妈妈跑的路程是7×20米;列方程:(20+8)×x=7×20,解方程,即可解答。
【详解】解:设小红的平均速度是x米/秒。
(20+8)×x=7×20
28x=140
x=140÷28
x=5
答:小红的平均速度是5米/秒。
【点睛】根据方程的实际应用,根据妈妈和小红跑的路程相同,利用速度、时间和路程三者的关系,设出未知数,列方程,解方程。
28.2.6米
【分析】由题意可知,此题用方程解答比较简单。一批布做了两种服装,数量之间存在的相等关系是:每套大人服装用布米数×套数+每套儿童服装用布米数×套数=布的总米数,据此列方程再依据等式的性质1和2解答即可。
【详解】解:设每套大人服装用布x米。
20x+25×2.2=107
20x+55=107
20x=52
x=2.6
答:每套大人服装用布2.6米。
【点睛】根据题意找出等量关系式是解答此题的关键。
29.28人
【分析】设参加唱红歌比赛的男生有x人,根据题意,男生人数的2.5倍-10人=参加唱红歌比赛的女生人数60。据此列方程解答。
【详解】解:设参加唱红歌比赛的男生有x人,
2.5x-10=60
2.5x=60+10
2.5x=70
x=28
答:参加唱红歌比赛的男生有28人。
【点睛】列方程解答问题的关键是找准等量关系,此题中男生人数的2.5倍-10人=参加唱红歌比赛的女生人数60人。
30.1.9厘米
【分析】设梯形的下底为b厘米,依据梯形的面积S=(a+b)×h÷2即可列方程求解。
【详解】解:设梯形的下底为b厘米,根据梯形面积公式列方程:
(0.5+b)×3÷2=3.6
1.5+3b=7.2
3b=5.7
b=1.9
答:下底长1.9厘米。
【点睛】此题考查了梯形的面积公式的实际应用。
31.小明95张;小芳19张
【分析】由题可知:小明的邮票数量是小芳的5倍,设小芳的邮票数量为x张,则小明的邮票数量为5x张,根据“小明的邮票-38张=小芳的邮票+38张”列方程解答。
【详解】解:设小芳的邮票数量为x张,则小明的邮票数量为5x张。
5x-38=x+38
5x-x=38+38
4x=76
x=19
小明的邮票:19×5=95(张)
答:小明原来有95张邮票,小芳原来有19张邮票。
【点睛】实际问题中的等量关系往往不是唯一的,要根据解决问题的需要进行选择。此外,画图、列表等都能帮助我们寻找等量关系。
32.48米
【分析】设甲队每天修x米,10天修10x米,乙队每天修24米,10天修24×10米,甲队10天修的米数+乙队10天修的米数=这条公路的长度,列方程:10x+24×10=720,解方程,即可解答。
【详解】10x+24×10=720
10x+240=720
10x=720-240
10x=480
x=480÷10
x=48
答:甲队每天修48米
【点睛】根据方程的实际应用,利用甲队和乙队用的天数相同,甲队修的米数与乙队修的米数的和等于这条路的全长,设出未知数,找出相关的量,列方程,解方程。
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、选择题(共10分)
1.(本题1分)小明做了x个灯笼,小军做了24个灯笼。小军送给小明4个后,两人的灯笼数就一样多了。下列方程正确的是( )。
A. B. C. D.
2.(本题1分)与方程x+0.8x=36有相同解的是( )。
A.1.68+x=3.98 B.x÷35=6.8 C.12x÷16=4.32 D.43-x=23
3.(本题1分)乐乐35张卡片,笑笑y张卡片,乐乐给笑笑4张后,两人卡片张数相同,下列方程正确的是( )。
A.35-y=4 B.y-8=35
C.y+4=35 D.y+4=35-4
4.(本题1分)下列式子中方程有( )个。
① ② ③ ④ ⑤
A.1 B.2 C.3 D.4
5.(本题1分)如果4x+1.4=4.2,那么18-10x=( )。
A.14 B.11 C.4 D.25
6.(本题1分)男生有x人,男生人数比女生人数的3倍多1人,女生有( )人。
A.3x+1 B.3x-1 C.(x-1)÷3 D.(x+1)÷3
7.(本题1分)a+7=b+4 ,那么a( )b。
A.大于 B.小于 C.等于 D.无法确定
8.(本题1分)在一个停车场,现停相同数量的四轮车和两轮车,两种车共有84个轮子,那么停车场两轮车有( )辆。
A.18 B.14 C.12 D.10
9.(本题1分)五年级两个班同学一共积肥1420千克,甲班有50人,平均每人积肥14千克,乙班有48人,平均每人积肥多少千克?
解:设乙班平均每人积肥x千克
列出方程正确的是( )
A.48x+14×50=1420 B.48x+14=1420 C.(x+14)×50=1420 D.x+14×50=1420
10.(本题1分)一辆大汽车每天运货10.5吨,是小汽车运货量的3.5倍,小汽车的运货量是( )
A.14吨 B.7吨 C.3吨 D.10吨
评卷人得分
二、填空题(共20分)
11.(本题2分)当X=( )时,7X与56相等,当X=( )时,7X-12与3X相等。
12.(本题2分)用方程表示数量关系。
一条裤子y元,一件上衣的价格是一条裤子的2.2倍,一件上衣比一条裤子贵60元( )。
13.(本题2分)若,则( )。
14.(本题2分)如果3个连续自然数的和是99,那么这3个数中最小的是( )。
15.(本题2分)在( )里填上“”“”或“”。
当时,( )30;( )32;
当时,( )0.12;( )0.2。
16.(本题2分)如果,那么( )。
17.(本题2分)在5+x>9,y-16=54,20+30=50中等式是( );方程是( )。
18.(本题2分)根据“一头牛重510千克,大约是一只羊重量的12倍”可以得到数量间的相等关系式是:( )的体重×12=( )的体重。
19.(本题2分)黄花有n朵,红花比黄花少8朵,红花有( )朵;如果黄花的朵数是20朵,红花有( )朵。
20.(本题2分)吴伟买了1本练习本和3支铅笔,张兰买了8支同样的铅笔,两人用去的钱同样多。1本练习本的价钱=1支铅笔的价钱×( )。
评卷人得分
三、看图列方程,并解答(共10分)
21.(本题5分)
22.(本题5分)
评卷人得分
四、解答题(共60分)
23.(本题6分)2021年6月17日9时22分,我国长征二号F运载火箭搭载神舟十二号载人飞船顺利升空,并取得圆满成功。火箭由四个助推器、芯一级火箭、芯三级火箭、整流罩和逃逸塔组成。火箭高58.34米,是助推器直径的25倍多2.09米,火箭助推器的直径是多少米?(列方程解答)
24.(本题6分)一个长方形的木板,如果长减少5分米,宽减少2分米,那么它的面积就减少66平方分米,这是剩下的部分恰好是一个正方形,求原来长方形的面积。
25.(本题6分)盒子里有相同数量的白子和黑子。每次取出5个白子和3个黑子。取了若干次后,白子没有了,黑子还剩16个。一共取了几次?(列方程解答)
26.(本题6分)图书馆买来科技书178本,比故事书的1.8倍少38本,图书馆买来故事书多少本?(用方程解)
27.(本题6分)小红和妈妈在400米环形跑道上的同一起点处跑步,为了体现公平,妈妈让小红先跑8秒然后才去追她,结果又用了20秒才第一次追上她。已知妈妈的平均速度是7米/秒,小红的平均速度是多少米/秒?
28.(本题6分)服装厂用107米蓝布做大人服装20套,儿童服装25套,已知每套儿童服装用布2.2米,每套大人服装用布多少米?
29.(本题6分)希望小学少先队员参加“建党100周年”唱红歌比赛,其中女生60人,比男生人数的2.5倍少10人。参加唱红歌比赛的男生多少人?(列方程解答)
30.(本题6分)一个梯形的面积3.6平方厘米,上底长0.5厘米,高3厘米,下底长多少厘米?(列方程解答)
31.(本题6分)小明和小芳是集邮爱好者,小明的邮票数量是小芳的5倍,如果小明给小芳38张,他们的邮票数量正好相等,小明和小芳原来各有多少张邮票?(用方程解)
32.(本题6分)甲乙两个工程队合修一段720米的公路,同时各从一端开始修,经过10天修完。乙队每天修24米,甲队每天修多少米?(列方程解答)
参考答案:
1.D
【分析】根据题意,小军的灯笼数量-4=小明的灯笼数量+4,据此列出方程。
【详解】根据题中的数量关系,应列方程为:或x+4+4=24。
故答案为:D
【点睛】找出题目中的等量关系式是列方程解应用题的关键。
2.D
【分析】解出方程方程x+0.8x=36的解,然后带入各选项,看等号的两边是否相等,以此判断。
【详解】x+0.8x=36
解:1.8x=36
x=20
A.1.68+20=21.68≠3.98
B.20÷35≈0.57≠6.8
C.12×20÷16
=240÷16
=15
15≠4.32
D.43-20=23
故答案为:D
【点睛】此题主要考查学生对检验方程解的掌握与应用。
3.D
【分析】乐乐给笑笑4张后,乐乐还有35-4张卡片,笑笑这时有y+4张卡片,由题意知:y+4=35-4。据此解答。
【详解】由分析知:
y+4=35-4
故答案为:D
【点睛】找出乐乐给笑笑4张后,乐乐现在有的卡片和笑笑现在有的卡片之间的等量关系是解答本题的关键。
4.C
【分析】根据方程的意义:含有未知数的等式,叫做方程;据此解答。
【详解】①55÷5=11,是等式,不含有未知数,不是方程;
②x+5<14,含有未知数,但不是等式,不是方程;
③8+a=10,既含有未知数,又是等式,是方程;
④5+36=x+35,既含有未知数,又是等式,是方程;
⑤x=5,既含有未知数,又是等式,是方程。
③、④、⑤有3个式子是方程。
故答案选:C
【点睛】本题考查方程的意义,根据方程的意义解答问题。
5.B
【分析】根据等式的性质,求出x的值,再代入18-10x求值即可。
【详解】4x+1.4=4.2
解:4x=4.2-1.4
x=2.8÷4
x=0.7
18-10x =18-10×0.7
=18-7
=11
故答案为:B
【点睛】本题主要考查根据等式的性质解方程。
6.C
【分析】根据题意女生人数的3倍加上1就是男生人数,所以女生人数就是男生人数减去1,然后再除以3,据此解答即可。
【详解】男生有x人,男生人数比女生人数的3倍多1人,女生有(x-1)÷3人。
故答案为:C
【点睛】本题重点考查了用字母表示数以及数量之间的关系。
7.B
【分析】等式的性质,等式两边同时加上或减去同一个数,等式仍然成立,再比较a与b的大小。
【详解】a+7=b+4,根据等式的性质1可得:
a+7-4=b+4-4
a+3=b
所以a<b。
故答案为:B
8.B
【分析】设两轮车有x辆,则四轮车也有x辆,两轮车的轮子个数为2x,四轮车的轮子个数为4x,相加等于84,据此列方程解答即可。
【详解】解:设两轮车有x辆,则四轮车也有x辆。
2x+4x=84
6x=84
x=14
故选择:B。
【点睛】此题考查了用方程解决实际问题,找出等量关系,分别表示出两种车轮子个数是解题关键。
9.A
【分析】题意可知,“两个班一共积肥1420千克”是本题的关键句。数量之间存在以下相等关系:乙班平均每人积肥数量×人数+甲班平均每人积肥数量×人数=两个班一共积肥数量。
【详解】由分析可知列方程如下:48x+14×50=1420
故选择:A
【点睛】此题考查列方程解决实际问题,找出等量关系,分别求出两个班施肥质量是解题关键。
10.C
【分析】已知大货车每天运货10.5吨,是小汽车运货量的3.5倍,那么大货车运的多,小汽车运的少,设小汽车运货量为x吨,大货车运的量是小汽车的3.5倍,3.5x=等于大货车运的量。
【详解】解:设小汽车的运货量是x吨,根据题意列方程:
3.5x=10.5
x=10.5÷3.5
x=3
故答案为:C。
【点睛】本题考查方程的意义,根据题意找出等量关系,列方程,解方程。
11. 8 3
【分析】要求X的值,即是求7X=56与7X-12=3X两个方程的解,利用等式性质解方程即可。
【详解】根据分析可知:
7X=56
解:7X÷7=56÷7
X=8
7X-12=3X
解:7X-12+12=3X+12
7X=3X+12
7X-3X=3X+12-3X
4X=12
4X÷4=12÷4
X=3
所以当X=8时,7X与56相等,当X=3时,7X-12与3X相等。
【点睛】本题考查利用等式性质解方程,关键是建立方程。
12.2.2y-y=60
【分析】一条裤子y元,一件上衣的价钱是一条裤子的2.2倍,一件上衣的价格是2.2y元,一件上衣比一条裤子贵60元,用上衣的价格-裤子的价格=60元,列方程:2.2y-y=60,据此解答。
【详解】解:设一条裤子y元。
2.2y-y=60
1.2y=60
y=60÷1.2
y=50
【点睛】本题考查方程的应用,根据上衣的价钱与裤子的价钱关系,列方程。
13.60
【分析】根据等式的性质1,方程的两边同时加上8,求出方程x-8=7的解,再把方程的解带入4x,即可解答。
【详解】x-8=7
解:x-8+=7+8
x=15
4x=4×15=60
【点睛】本题考查解方程,根据等式的性质1,解方程,求出方程的解,进而求出4x的值。
14.32
【分析】设中间的自然数为x,找到关系式第一个自然数+中间的自然数+第三个自然数=99,列方程解答。
【详解】解:设中间的自然数为x。
x-1+x+x+1=99
3x=99
x=33
最小的数:33-1=32
【点睛】分析题意,找到合适的量设为未知数并列出等量关系式是列方程解题的重要步骤。
15. > > = <
【分析】根据题意,把x=12,带入式子x+19,计算出结果再和30比较大小;把x=12,带入式子60-x,求出结果再和32比较大小;
把x=0.2,带入式子0.6x,求出结果,再和0.12比较大小;把x=0.2,代入式子x÷0.2,求出结果,再和0.2比较大小;即可解答。
【详解】当x=12时
12+19=31;因为31>30,所以x+19>30
当x=12时
60-12=48,因为48>32,所以60-x>32
当x=0.2时
0.6×0.2=0.12,因为0.12=0.12,所以0.6x=0.12
当x=0.2时
0.2÷2=0.1,因为0.1<0.2,所以x÷0.2<0.2
【点睛】本题考查含有字母式子的化简与求值,以及两位数比较大小,小数比较大小。
16.56
【分析】先求得方程的解,再将解代入中,据此解答。
【详解】
解:
将代入中,
=54+2=56
【点睛】求得方程的解,是解答此题的关键。
17. y-16=54;20+30=50 y-16=54
【分析】根据方程和等式的意义:等式是指用等号连接的式子;方程是指含有未知数的等式;所有的方程都是等式,但等式不一定是方程;据此解答。
【详解】在5+x>9,y-16=54,20+30=50中等式是y-16=54;20+30=50;方程是y-16=54。
【点睛】本题考查等式和方程的意义,方程是等式,但等式不一定是方程。
18. 一只羊 一头牛
【分析】根据题意可知,一头牛的重量是一只羊重量的12倍。
【详解】根据分析可知,一只羊的体重×12=一头牛的体重。
【点睛】此题主要考查等式的认识及列等量关系式。
19. n-8 12
【分析】根据题意,黄花有n朵,红花比黄花少8朵,用黄花的朵数-8=红花的朵数;即n-8=红花朵数;如果黄花的朵数20朵,带入n-8式子,即可求出红花的朵数,据此解答。
【详解】红花有:n-8(朵)
黄花的朵数20朵,黄花有:20-8=12(朵)
【点睛】本题考查用字母表示数,以及含有字母的式子化简与求值。
20.5
【分析】根据题意可知,因为1本练习本的价钱+3支铅笔的价钱=8支铅笔的价钱,所以8支铅笔的价钱-3支铅笔的价钱=5支铅笔的价钱=1个练习本的价钱。
【详解】根据分析可知,1本练习本的价钱=5支铅笔的价钱=1支铅笔的价钱×5。
【点睛】此题主要考查学生对等量代换的应用。
21.3x=50-5
x=15
【分析】由于50元买了3个西瓜,还找回5元,那么相当于3个西瓜的价钱=50-5,据此即可列方程,再根据等式的性质解方程即可。
【详解】3x=50-5
解:3x=45
x=45÷3
x=15
每个西瓜15元。
22.50.8元
【分析】设面粉的钱数是x元,已知大米是面粉价钱的4倍,则面粉的价钱是4x元,由图可知:面粉的钱数加上大米的钱数共254元,据此列出方程并求解即可。
【详解】解:设面粉的钱数是x元,根据题意列方程如下:
x+4x=254
5x=254
x=50.8
面粉的钱数是50.8元。
23.2.25米
【分析】根据“火箭高58.34米,是助推器直径的25倍多2.09米”这一信息,可分析出此题等量关系为:助推器的直径×25+2.09=火箭的高度,设火箭助推器的直径是x米,列出方程并依据等式的性质1和2解答即可。
【详解】解:设火箭助推器的直径是x米。
25x+2.09=58.34
25x+2.09-2.09=58.34-2.09
25x=56.25
25x÷25=56.25÷25
x=2.25
答:火箭助推器的直径是2.25米。
【点睛】此题重点考查列方程解决实际问题的能力,关键是要找准等量关系式。
24.130平方分米
【分析】如图所示,设正方形的边长为a厘米,则减少的面积为长和宽分别是(a+5)分米、2分米与a分米、5分米的两个长方形的面积和,据此就可列等式求出a的值,从而求出原来长方形的面积。
【详解】解:设正方形的边长为a分米。
则(a+5)×2+5a=66
2a+10+5a=66
7a=66-10
7a=56
a=56÷7
a=8
原长方形的面积:(8+5)×(8+2)
=13×10
=130(平方分米)
答:原来长方形的面积是130平方分米。
【点睛】解决此题的关键是先求出正方形的边长,进而求得原长方形的面积。
25.8次
【分析】设一共取了x次,白子全部被取出,可知白子一共5x个,黑子数量是(3x+16)个,列出等量关系式,解方程即可。
【详解】解:设一共取了x次。
5x=3x+16
2x=16
x=8
答:一共取了8次。
【点睛】根据白子和黑子总数量相等列出等量关系是解题的关键。
26.120本
【分析】根据题意,设图书馆买来故事书x本,科技书比故事书的1.8倍少38本,就是故事书×1.8再减去38本等于科技书的本数,列方程:1.8x-38=178,解方程,即可解答。
【详解】解:设图书馆买来故事书x本。
1.8x-38=178
1.8x=178+38
1.8x=216
x=216÷1.8
x=120
答:图书馆买来故事书120本。
【点睛】根据方程的实际应用,利用买来的故事书与科技书之间的关系,设出未知数,列方程,解方程。
27.5米/秒
【分析】根据题意,妈妈跑了20秒,妈妈的平均速度是7米/秒,用7×20,求出妈妈跑的路程;小红跑了8+20秒,小红跑的路程和妈妈跑的路程一样长,设:小红的平均速度是x米/秒;小红跑的路程是(20+8)×x米;妈妈跑的路程是7×20米;列方程:(20+8)×x=7×20,解方程,即可解答。
【详解】解:设小红的平均速度是x米/秒。
(20+8)×x=7×20
28x=140
x=140÷28
x=5
答:小红的平均速度是5米/秒。
【点睛】根据方程的实际应用,根据妈妈和小红跑的路程相同,利用速度、时间和路程三者的关系,设出未知数,列方程,解方程。
28.2.6米
【分析】由题意可知,此题用方程解答比较简单。一批布做了两种服装,数量之间存在的相等关系是:每套大人服装用布米数×套数+每套儿童服装用布米数×套数=布的总米数,据此列方程再依据等式的性质1和2解答即可。
【详解】解:设每套大人服装用布x米。
20x+25×2.2=107
20x+55=107
20x=52
x=2.6
答:每套大人服装用布2.6米。
【点睛】根据题意找出等量关系式是解答此题的关键。
29.28人
【分析】设参加唱红歌比赛的男生有x人,根据题意,男生人数的2.5倍-10人=参加唱红歌比赛的女生人数60。据此列方程解答。
【详解】解:设参加唱红歌比赛的男生有x人,
2.5x-10=60
2.5x=60+10
2.5x=70
x=28
答:参加唱红歌比赛的男生有28人。
【点睛】列方程解答问题的关键是找准等量关系,此题中男生人数的2.5倍-10人=参加唱红歌比赛的女生人数60人。
30.1.9厘米
【分析】设梯形的下底为b厘米,依据梯形的面积S=(a+b)×h÷2即可列方程求解。
【详解】解:设梯形的下底为b厘米,根据梯形面积公式列方程:
(0.5+b)×3÷2=3.6
1.5+3b=7.2
3b=5.7
b=1.9
答:下底长1.9厘米。
【点睛】此题考查了梯形的面积公式的实际应用。
31.小明95张;小芳19张
【分析】由题可知:小明的邮票数量是小芳的5倍,设小芳的邮票数量为x张,则小明的邮票数量为5x张,根据“小明的邮票-38张=小芳的邮票+38张”列方程解答。
【详解】解:设小芳的邮票数量为x张,则小明的邮票数量为5x张。
5x-38=x+38
5x-x=38+38
4x=76
x=19
小明的邮票:19×5=95(张)
答:小明原来有95张邮票,小芳原来有19张邮票。
【点睛】实际问题中的等量关系往往不是唯一的,要根据解决问题的需要进行选择。此外,画图、列表等都能帮助我们寻找等量关系。
32.48米
【分析】设甲队每天修x米,10天修10x米,乙队每天修24米,10天修24×10米,甲队10天修的米数+乙队10天修的米数=这条公路的长度,列方程:10x+24×10=720,解方程,即可解答。
【详解】10x+24×10=720
10x+240=720
10x=720-240
10x=480
x=480÷10
x=48
答:甲队每天修48米
【点睛】根据方程的实际应用,利用甲队和乙队用的天数相同,甲队修的米数与乙队修的米数的和等于这条路的全长,设出未知数,找出相关的量,列方程,解方程。
