7 解决问题(三)(课件)六年级上册数学人教版(共21张PPT)
文档属性
| 名称 | 7 解决问题(三)(课件)六年级上册数学人教版(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 16:14:20 | ||
图片预览








文档简介
(共21张PPT)
7 解决问题(三)
第三单元 分数除法
1.经历探索解决“已知两个未知量的倍数关系及和(或差)的关系,求这两个未知量”这一实际问题的过程,掌握用字母和代数式表示题中两个未知量的方法,能充分利用两个等量关系列方程进行解答。
2.在阅读、理解、分析、解答、回顾、反思等活动中体会方程的思想和价值,体验解题方法的多样化,提高解决实际问题的能力。
3.积累相关解决问题的经验,体会数学与现实生活的联系,增强应用意识。
温习旧知
解决问题。
1.小红采集了24件标本,比小刚采集的标本多,小刚采集了多少件标本?
24÷(1+)=18(件)
答:小刚采集了18件标本。
2.参加田径比赛的有54人,比参加球类比赛的人数少。参加球类比赛的有多少人?
54÷(1-)=72(人)
答:参加球类比赛的有72人。
知识链接
木桶定律也可称为短板效应,是指一个木桶能装多少水取决于它最短的那块木板。一个木桶想盛满水,必须每块木板都一样平齐且无破损,如果这个桶的木板中有一块不齐或者某块木板下面有破洞,这个桶就无法盛满水。任何一个组织都可能面临一个共同的问题,即构成组织的各个部分往往是优劣不齐的,而劣势部分往往决定整个组织的水平。
预习新知
一、课前自学例6,完成温习旧知,回忆之前两个课时用分数除法解决问题的方法和步骤。
二、课堂中和同学合作交流分析题意,合作探究解题思路,提高分析问题的能力。
三、课堂中和老师一起总结“已知两个未知量的倍数关系及和(或差)的关系,求这两个未知量”的问题的解题思路和方法,提高解决问题的能力。
任务驱动一:阅读教材例6,从图中你能了解到哪些信息?哪些信息是未知的?
已知信息:六年级举行篮球比赛。六(1)班全场得了42分,下半场得分是上半场的一半。
未知信息:六(1)班上半场和下半场各得多少分?
任务驱动二:要求上半场和下半场的得分情况,也就是要求两个未知数,你能根据“下半场得分是上半场的一半”画出线段图吗?你能根据线段图列出数量关系式吗?
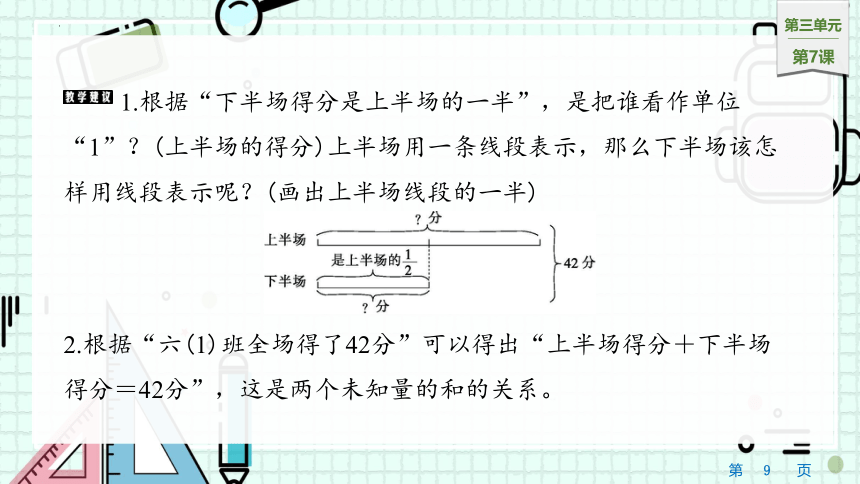
1.根据“下半场得分是上半场的一半”,是把谁看作单位“1”?(上半场的得分)上半场用一条线段表示,那么下半场该怎样用线段表示呢?(画出上半场线段的一半)
2.根据“六(1)班全场得了42分”可以得出“上半场得分+下半场得分=42分”,这是两个未知量的和的关系。
3.根据“下半场得分是上半场的一半”可以得出“下半场得分=上半场得分×或上半场得分=下半场得分×2”,这是两个未知量的倍数关系。
4.师:如果列方程来解决,你想设哪个量为未知数?另一个量怎么表示?方程又该怎么列呢?
方法一:设上半场得x分,则下半场得x分。方法二:设下半场得x分,则上半场得 2x分。
x=42÷
x=28
28×=14(分)
2x+x=42
3x=42
x=14
42-14=28(分)
x+x=42
x=42
5.师:你还能根据“和(或差)的关系”来列方程吗?
方法一:设上半场得x分,则下半场得(42-x)分,再根据“和(或差)的关系”列出方程42-x=x。
方法二:设下半场得x分,则上半场得(42-x)分,再根据“和(或差)的关系”列出方程42-x=2x。
任务驱动三:怎样检验解法是否正确呢?思考方程的解题思路,你有什么发现?
28+14=42(分),全场得分是42分。14÷28=,下半场得分是上半场的一半。
两个方程所用数量关系式相同,但设的未知数不同,是因为对“下半场得分是上半场的一半”这句话有不同的解读。
解决含有两个未知数的实际问题,可以利用两个未知量的倍数关系,或者利用两个未知量的和(或差)的关系。设一个量为未知数x,用代数式表示出另一个量,列出方程,解方程,最后检验方程。
在解决此类应用题时,我们通常假设单位“1”的量为未知数x,另一个量则为x的几分之几,这样不容易出错。
一、解方程。
x×=3 x-x= x+x=×
x=
x=
x=
二、解决问题。
1.东川区第一小学鼓号队共有48人,其中男生人数是女生人数的。鼓号队中男生和女生各有多少人?(用方程解答)
解:设女生有x人。
x+x=48
x=30 48-30=18(人)
答:女生有30人,男生有18人。
2.一个书架有上、下两层,下层书的本数是上层书的本数的。如果把上层的书搬30本放到下层,那么两层书的本数同样多。原来上、下两层各有多少本书?(先把线段图补充完整,再解答)( 实践类作业)
上层:30×2÷(1-)=100(本) 下层:100×=40(本)
答:原来上层有100本书,下层有40本书。
3.一场跳绳比赛中,金金和阳阳一共跳了212个,其中金金跳的个数比阳阳的一半多20个。他们分别跳了多少个?
解:设阳阳跳了x个,则金金跳了(x+20)个。
x+(x+20)=212
x=128
金金:128×+20=84(个)
答:阳阳跳了128个,金金跳了84个。
4.2022年北京冬奥会,中国有176名运动员参赛,其中男运动员的人数比女运动员的多31人。男运动员和女运动员分别有多少人?( 拓展类作业)
解:设女运动员有x人。
x+(x+31)=176
x=87
男运动员:87×+31=89(人)
答:男运动员有89人,女运动员有87人。
END
感谢观看 下节课再会
7 解决问题(三)
第三单元 分数除法
1.经历探索解决“已知两个未知量的倍数关系及和(或差)的关系,求这两个未知量”这一实际问题的过程,掌握用字母和代数式表示题中两个未知量的方法,能充分利用两个等量关系列方程进行解答。
2.在阅读、理解、分析、解答、回顾、反思等活动中体会方程的思想和价值,体验解题方法的多样化,提高解决实际问题的能力。
3.积累相关解决问题的经验,体会数学与现实生活的联系,增强应用意识。
温习旧知
解决问题。
1.小红采集了24件标本,比小刚采集的标本多,小刚采集了多少件标本?
24÷(1+)=18(件)
答:小刚采集了18件标本。
2.参加田径比赛的有54人,比参加球类比赛的人数少。参加球类比赛的有多少人?
54÷(1-)=72(人)
答:参加球类比赛的有72人。
知识链接
木桶定律也可称为短板效应,是指一个木桶能装多少水取决于它最短的那块木板。一个木桶想盛满水,必须每块木板都一样平齐且无破损,如果这个桶的木板中有一块不齐或者某块木板下面有破洞,这个桶就无法盛满水。任何一个组织都可能面临一个共同的问题,即构成组织的各个部分往往是优劣不齐的,而劣势部分往往决定整个组织的水平。
预习新知
一、课前自学例6,完成温习旧知,回忆之前两个课时用分数除法解决问题的方法和步骤。
二、课堂中和同学合作交流分析题意,合作探究解题思路,提高分析问题的能力。
三、课堂中和老师一起总结“已知两个未知量的倍数关系及和(或差)的关系,求这两个未知量”的问题的解题思路和方法,提高解决问题的能力。
任务驱动一:阅读教材例6,从图中你能了解到哪些信息?哪些信息是未知的?
已知信息:六年级举行篮球比赛。六(1)班全场得了42分,下半场得分是上半场的一半。
未知信息:六(1)班上半场和下半场各得多少分?
任务驱动二:要求上半场和下半场的得分情况,也就是要求两个未知数,你能根据“下半场得分是上半场的一半”画出线段图吗?你能根据线段图列出数量关系式吗?
1.根据“下半场得分是上半场的一半”,是把谁看作单位“1”?(上半场的得分)上半场用一条线段表示,那么下半场该怎样用线段表示呢?(画出上半场线段的一半)
2.根据“六(1)班全场得了42分”可以得出“上半场得分+下半场得分=42分”,这是两个未知量的和的关系。
3.根据“下半场得分是上半场的一半”可以得出“下半场得分=上半场得分×或上半场得分=下半场得分×2”,这是两个未知量的倍数关系。
4.师:如果列方程来解决,你想设哪个量为未知数?另一个量怎么表示?方程又该怎么列呢?
方法一:设上半场得x分,则下半场得x分。方法二:设下半场得x分,则上半场得 2x分。
x=42÷
x=28
28×=14(分)
2x+x=42
3x=42
x=14
42-14=28(分)
x+x=42
x=42
5.师:你还能根据“和(或差)的关系”来列方程吗?
方法一:设上半场得x分,则下半场得(42-x)分,再根据“和(或差)的关系”列出方程42-x=x。
方法二:设下半场得x分,则上半场得(42-x)分,再根据“和(或差)的关系”列出方程42-x=2x。
任务驱动三:怎样检验解法是否正确呢?思考方程的解题思路,你有什么发现?
28+14=42(分),全场得分是42分。14÷28=,下半场得分是上半场的一半。
两个方程所用数量关系式相同,但设的未知数不同,是因为对“下半场得分是上半场的一半”这句话有不同的解读。
解决含有两个未知数的实际问题,可以利用两个未知量的倍数关系,或者利用两个未知量的和(或差)的关系。设一个量为未知数x,用代数式表示出另一个量,列出方程,解方程,最后检验方程。
在解决此类应用题时,我们通常假设单位“1”的量为未知数x,另一个量则为x的几分之几,这样不容易出错。
一、解方程。
x×=3 x-x= x+x=×
x=
x=
x=
二、解决问题。
1.东川区第一小学鼓号队共有48人,其中男生人数是女生人数的。鼓号队中男生和女生各有多少人?(用方程解答)
解:设女生有x人。
x+x=48
x=30 48-30=18(人)
答:女生有30人,男生有18人。
2.一个书架有上、下两层,下层书的本数是上层书的本数的。如果把上层的书搬30本放到下层,那么两层书的本数同样多。原来上、下两层各有多少本书?(先把线段图补充完整,再解答)( 实践类作业)
上层:30×2÷(1-)=100(本) 下层:100×=40(本)
答:原来上层有100本书,下层有40本书。
3.一场跳绳比赛中,金金和阳阳一共跳了212个,其中金金跳的个数比阳阳的一半多20个。他们分别跳了多少个?
解:设阳阳跳了x个,则金金跳了(x+20)个。
x+(x+20)=212
x=128
金金:128×+20=84(个)
答:阳阳跳了128个,金金跳了84个。
4.2022年北京冬奥会,中国有176名运动员参赛,其中男运动员的人数比女运动员的多31人。男运动员和女运动员分别有多少人?( 拓展类作业)
解:设女运动员有x人。
x+(x+31)=176
x=87
男运动员:87×+31=89(人)
答:男运动员有89人,女运动员有87人。
END
感谢观看 下节课再会
