苏教版小学数学五年级下册1.《简易方程》周末作业(含答案解析)
文档属性
| 名称 | 苏教版小学数学五年级下册1.《简易方程》周末作业(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-17 00:00:00 | ||
图片预览


文档简介
苏教版数学五下第一单元《简易方程》周末作业(二)
学校:___________姓名:___________班级:___________
一、选择题
1.爸爸有86张邮票,送给贝贝24张邮票后两人的邮票同样多。设贝贝原来有x张邮票,下列方程错误的是( )。
A.86-24=24+x B.86-24=x C.86-x=24×2
2.甲、乙两人年龄的和为27岁,已知甲的年龄比乙的年龄的2倍少3岁,求甲、乙两人各几岁。设乙的年龄为x岁,列方程是( )。
A.2x+3+x=27 B.2x-3+x=27 C.2x-3-x=27
3.方程15.6-x=15.6的解是( )。
A.x=15.6 B.x=31.2 C.x=0
4.等式两边都除以( )数,所得的结果仍然是等式。
A.任何 B.同一个 C.同一个不为0的
5.下列各式中,是方程的是( )。
A.7x-3=0 B.x-1>1 C.7.2x-3.8x
二、填空题
6.根据等式的性质在横线上填运算符号,在括号里填数。
x—35=50
解:x-35+35=50____( )
x=( )
0.5x=7.5
解:0.5x÷0.5=7.5____( )
x=( )
7.三个连续奇数的和是3m,这三个奇数中,最大的一个数是( )。
8.若x=2是方程4x+3a=26的解,则a=( )。
9.要使方程y-□=1.6的解为y=3.5,则□=________。
10.白兔是黑兔的4倍,黑兔比白兔少360只,列方程解答时,可设________为x只,列方程为________,解得白兔有________只。
三、看图列方程并解答
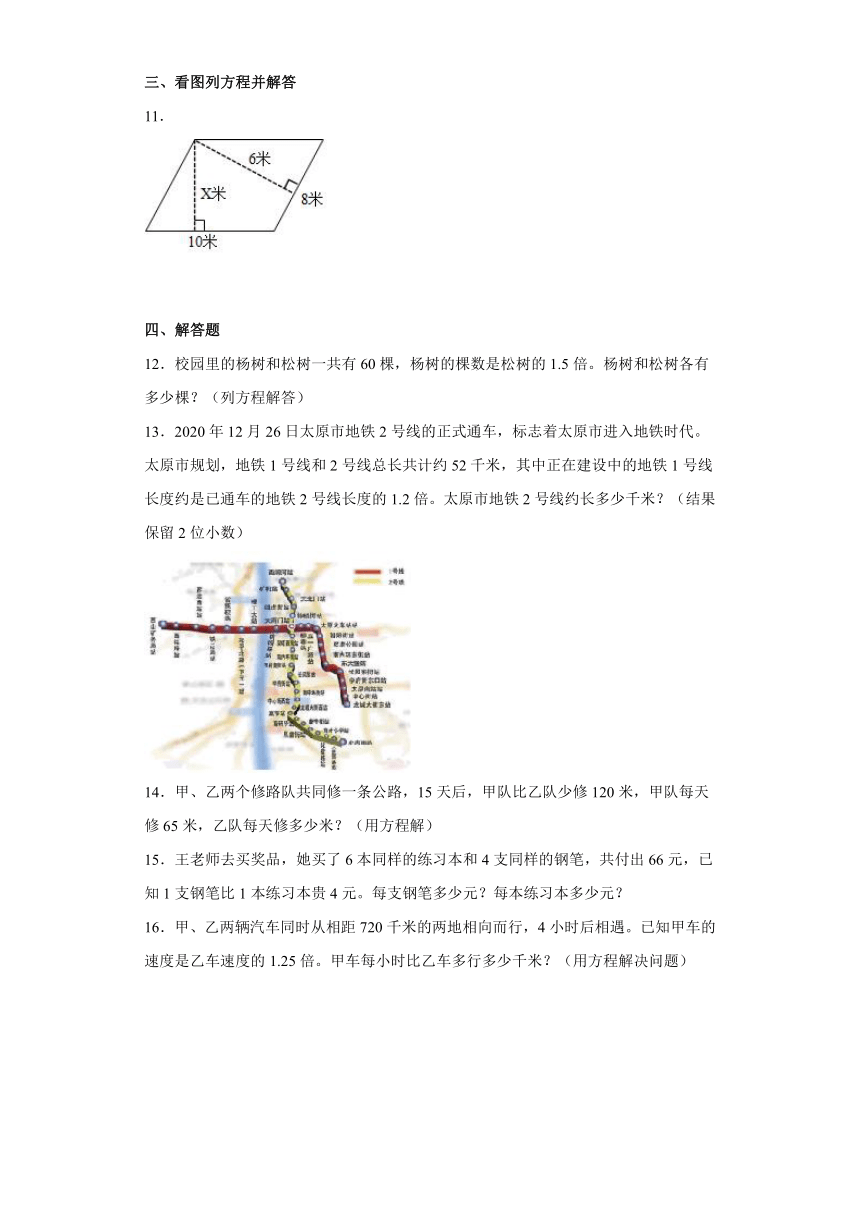
11.
四、解答题
12.校园里的杨树和松树一共有60棵,杨树的棵数是松树的1.5倍。杨树和松树各有多少棵?(列方程解答)
13.2020年12月26日太原市地铁2号线的正式通车,标志着太原市进入地铁时代。太原市规划,地铁1号线和2号线总长共计约52千米,其中正在建设中的地铁1号线长度约是已通车的地铁2号线长度的1.2倍。太原市地铁2号线约长多少千米?(结果保留2位小数)
14.甲、乙两个修路队共同修一条公路,15天后,甲队比乙队少修120米,甲队每天修65米,乙队每天修多少米?(用方程解)
15.王老师去买奖品,她买了6本同样的练习本和4支同样的钢笔,共付出66元,已知1支钢笔比1本练习本贵4元。每支钢笔多少元?每本练习本多少元?
16.甲、乙两辆汽车同时从相距720千米的两地相向而行,4小时后相遇。已知甲车的速度是乙车速度的1.25倍。甲车每小时比乙车多行多少千米?(用方程解决问题)
参考答案:
1.B
【解析】设贝贝原来有x张邮票,分析出等量关系式:爸爸的邮票张数-24=贝贝的邮票张数+24,或者爸爸的邮票张数-贝贝的邮票张数=24×2,据此列出方程判断。
【详解】A.86-24=24+x,列方程正确;
B. 86-24=x,86-24为爸爸现在的邮票,应该等于贝贝现在的邮票:24+x,列方程错误;
C.86-x=24×2,列方程正确。
故答案为:B
【点睛】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题。
2.B
【解析】设乙的年龄为x岁,那么甲的年龄为(2x-3)岁,等量关系式为:甲的年龄+乙的年龄=27,据此列方程判断。
【详解】设乙的年龄为x岁.
甲的年龄:2×x-3=(2x-3)岁,
列方程:2x-3+x=27。
故答案为;B
【点睛】列方程解应用题,若在题干中含有两个未知量的情况下,在设出一个量为未知量x时,一定要将其它的量用x表示出来。
3.C
【解析】等式两边同时加上或减去同一个数,所得结果还是等式,据此解答。
【详解】15.6-x=15.6
解:15.6-x+x=15.6+x
15.6+x=15.6
15.6+x-15.6=15.6-15.6
x=0
故答案为:C
【点睛】等式的性质是解方程的一种有效的方法,学生应熟练掌握。
4.C
【解析】根据等式两边同时乘以或除以同一个不为0的数,所得结果还是等式,来作答。
【详解】除数不能为0,所以等式两边都除以同一个不为0的数,所得的结果仍然是等式。
故答案为:C
【点睛】此题考查等式的性质,要注意:除以一个相同的数时,此数不等于0。
5.A
【解析】含有未知数的等式叫做方程,据此解答。
【详解】A.7x-3=0,是方程;
B.x-1>1,是不等式;
C. 7.2x-3.8x,不是等式,不是方程。
故答案为:A
【点睛】方程的定义是解答此题的关键,注意:方程必须是等式;必须含有未知数。
6. + 35 85 ÷ 0.5 15
【分析】等式的性质:(1)等式两边同时加上或减去同一个数,所得结果还是等式;(2)等式两边同时乘以或除以同一个不为0的数,所得结果还是等式。
【详解】x—35=50
解:x-35+35=50+35
x=85
0.5x=7.5
解:0.5x÷0.5=7.5÷0.5
x=15
【点睛】等式的性质是解方程的主要依据,学生应熟练掌握。
7.m+2
【分析】三个连续奇数的和是3m,则中间的奇数是m,又连续奇数相差2;据此求出最大奇数。
【详解】中间奇数为:3m÷3=m,连续奇数相差2,所以最大的一个数是m+2。
【点睛】理解连续奇数相差2是解题的关键。
8.6
【分析】将x=2代入原方程,列出含有未知数a的方程,解方程即可求出a的值。
【详解】将x=2代入原方程得:
8+3a=26
3a=26-8
a=18÷3
a=6
所以,a=6。
【点睛】本题主要考查方程的解法,根据数据、符号的特点灵活应用等式的性质求解即可。
9.1.9
【分析】把y=3.5代入方程y-□=1.6,把□看作未知数,解方程即可。
【详解】由题意可得:
3.5-□=1.6
解:□=3.5-1.6
□=1.9
【点睛】学会把题目变形,解此方程主要依据等式两边同时加或减相同的数,等式仍然成立。
10. 黑兔 4x-x=360 480
【分析】列方程时,根据数量关系,一般把1倍的量设为未知数,等量关系为白兔数量-黑兔数量=360,据此解答。
【详解】白兔是黑兔的4倍,黑兔比白兔少360只,列方程解答时,可设黑兔为x只,列方程为4x-x=360,3x=360,x=120,白兔:4x=120×4=480,解得白兔有480只。
【点睛】列方程的关键是找出等量关系,解方程主要是依据等式的性质,等式两边同时乘或除同一个不为0的数,等式仍然成立;等式两边同时加或减相同的数,等式仍然成立。
11.x=4.8
【分析】平行四边形的面积=底×高。图中10米和x米、8米和6米是两组对应的底和高,则这两组数的乘积相等,据此列方程解答。
【详解】解:10x=8×6
10x=48
x=4.8
12.杨树有36棵;松树有24棵
【分析】根据题意,设松树有x棵,则杨树有1.5x棵,杨树与松树一共有60棵,列方程:x+1.5x=60,解方程,即可解答。
【详解】解:设松树有x棵,则杨树有1.5x棵
x+1.5x=60
2.5x=60
x=60÷2.5
x=24
杨树有:2.4×15=36(棵)
答:杨树有36棵,松树有24棵。
【点睛】本题考查方程的实际应用,根据题意,找出相关的量,列方程,解方程。
13.23.64千米
【分析】本题用方程解答比较简便。设地铁2号线长为x米,则1号线长为1.2x千米。根据1号线的长度+2号线的长度=52,据此列方程解答。
【详解】解:设地铁2号线长为x米,则1号线长为1.2x千米。
2.2x=52
答:太原市地铁2号线约长23.64千米。
【点睛】列方程解含有两个未知数的问题时,设其中的一个未知数是x,用含有x的式子表示另一个未知数,再根据等量关系即可列出方程。
14.73米
【分析】设乙队每天修x米,等量关系为:甲队、乙队每天修路的差×天数=120米,据此列方程解答。
【详解】解:设乙队每天修x米。
(x-65)×15=120
x-65=8
x=73
答:乙队每天修73米。
【点睛】列方程是解答应用题的一种有效的方法,解题的关键是弄清题意,找出应用题中的等量关系。
15.钢笔9元;练习本5元
【分析】设每本练习本x元,则每支钢笔(x+4)元,根据总价=单价×数量,分别求出钢笔和练习本花的钱数,相加等于66元,列方程解答即可。
【详解】解:设每本练习本x元,则每支钢笔(x+4)元。
6x+4(x+4)=66
6x+4x+16=66
10x=50
x=5
x+4=5+4=9
答:每支钢笔9元,每本练习本5元。
【点睛】此题考查了列方程解决实际问题,分别用未知数表示出两个量,找出等量关系解答即可。
16.20千米
【分析】根据速度和×相遇时间=两地之间的路程,设乙车每小时行驶x千米,则甲车每小时行驶1.25x千米,据此列方程解答即可。
【详解】解:设乙每小时行驶x千米,那么甲每小时行驶1.25x千米。
4(x+1.25x)=720
4×2.25x=720
x=80
1.25x=80×1.25=100(千米/时)
100-80=20(千米/时)
答:甲车每小时比乙车多行20千米。
【点睛】此题考查的目的是理解列方程解决问题的方法及应用,关键是找出等量关系,设出未知数,列方程解决问题。
学校:___________姓名:___________班级:___________
一、选择题
1.爸爸有86张邮票,送给贝贝24张邮票后两人的邮票同样多。设贝贝原来有x张邮票,下列方程错误的是( )。
A.86-24=24+x B.86-24=x C.86-x=24×2
2.甲、乙两人年龄的和为27岁,已知甲的年龄比乙的年龄的2倍少3岁,求甲、乙两人各几岁。设乙的年龄为x岁,列方程是( )。
A.2x+3+x=27 B.2x-3+x=27 C.2x-3-x=27
3.方程15.6-x=15.6的解是( )。
A.x=15.6 B.x=31.2 C.x=0
4.等式两边都除以( )数,所得的结果仍然是等式。
A.任何 B.同一个 C.同一个不为0的
5.下列各式中,是方程的是( )。
A.7x-3=0 B.x-1>1 C.7.2x-3.8x
二、填空题
6.根据等式的性质在横线上填运算符号,在括号里填数。
x—35=50
解:x-35+35=50____( )
x=( )
0.5x=7.5
解:0.5x÷0.5=7.5____( )
x=( )
7.三个连续奇数的和是3m,这三个奇数中,最大的一个数是( )。
8.若x=2是方程4x+3a=26的解,则a=( )。
9.要使方程y-□=1.6的解为y=3.5,则□=________。
10.白兔是黑兔的4倍,黑兔比白兔少360只,列方程解答时,可设________为x只,列方程为________,解得白兔有________只。
三、看图列方程并解答
11.
四、解答题
12.校园里的杨树和松树一共有60棵,杨树的棵数是松树的1.5倍。杨树和松树各有多少棵?(列方程解答)
13.2020年12月26日太原市地铁2号线的正式通车,标志着太原市进入地铁时代。太原市规划,地铁1号线和2号线总长共计约52千米,其中正在建设中的地铁1号线长度约是已通车的地铁2号线长度的1.2倍。太原市地铁2号线约长多少千米?(结果保留2位小数)
14.甲、乙两个修路队共同修一条公路,15天后,甲队比乙队少修120米,甲队每天修65米,乙队每天修多少米?(用方程解)
15.王老师去买奖品,她买了6本同样的练习本和4支同样的钢笔,共付出66元,已知1支钢笔比1本练习本贵4元。每支钢笔多少元?每本练习本多少元?
16.甲、乙两辆汽车同时从相距720千米的两地相向而行,4小时后相遇。已知甲车的速度是乙车速度的1.25倍。甲车每小时比乙车多行多少千米?(用方程解决问题)
参考答案:
1.B
【解析】设贝贝原来有x张邮票,分析出等量关系式:爸爸的邮票张数-24=贝贝的邮票张数+24,或者爸爸的邮票张数-贝贝的邮票张数=24×2,据此列出方程判断。
【详解】A.86-24=24+x,列方程正确;
B. 86-24=x,86-24为爸爸现在的邮票,应该等于贝贝现在的邮票:24+x,列方程错误;
C.86-x=24×2,列方程正确。
故答案为:B
【点睛】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题。
2.B
【解析】设乙的年龄为x岁,那么甲的年龄为(2x-3)岁,等量关系式为:甲的年龄+乙的年龄=27,据此列方程判断。
【详解】设乙的年龄为x岁.
甲的年龄:2×x-3=(2x-3)岁,
列方程:2x-3+x=27。
故答案为;B
【点睛】列方程解应用题,若在题干中含有两个未知量的情况下,在设出一个量为未知量x时,一定要将其它的量用x表示出来。
3.C
【解析】等式两边同时加上或减去同一个数,所得结果还是等式,据此解答。
【详解】15.6-x=15.6
解:15.6-x+x=15.6+x
15.6+x=15.6
15.6+x-15.6=15.6-15.6
x=0
故答案为:C
【点睛】等式的性质是解方程的一种有效的方法,学生应熟练掌握。
4.C
【解析】根据等式两边同时乘以或除以同一个不为0的数,所得结果还是等式,来作答。
【详解】除数不能为0,所以等式两边都除以同一个不为0的数,所得的结果仍然是等式。
故答案为:C
【点睛】此题考查等式的性质,要注意:除以一个相同的数时,此数不等于0。
5.A
【解析】含有未知数的等式叫做方程,据此解答。
【详解】A.7x-3=0,是方程;
B.x-1>1,是不等式;
C. 7.2x-3.8x,不是等式,不是方程。
故答案为:A
【点睛】方程的定义是解答此题的关键,注意:方程必须是等式;必须含有未知数。
6. + 35 85 ÷ 0.5 15
【分析】等式的性质:(1)等式两边同时加上或减去同一个数,所得结果还是等式;(2)等式两边同时乘以或除以同一个不为0的数,所得结果还是等式。
【详解】x—35=50
解:x-35+35=50+35
x=85
0.5x=7.5
解:0.5x÷0.5=7.5÷0.5
x=15
【点睛】等式的性质是解方程的主要依据,学生应熟练掌握。
7.m+2
【分析】三个连续奇数的和是3m,则中间的奇数是m,又连续奇数相差2;据此求出最大奇数。
【详解】中间奇数为:3m÷3=m,连续奇数相差2,所以最大的一个数是m+2。
【点睛】理解连续奇数相差2是解题的关键。
8.6
【分析】将x=2代入原方程,列出含有未知数a的方程,解方程即可求出a的值。
【详解】将x=2代入原方程得:
8+3a=26
3a=26-8
a=18÷3
a=6
所以,a=6。
【点睛】本题主要考查方程的解法,根据数据、符号的特点灵活应用等式的性质求解即可。
9.1.9
【分析】把y=3.5代入方程y-□=1.6,把□看作未知数,解方程即可。
【详解】由题意可得:
3.5-□=1.6
解:□=3.5-1.6
□=1.9
【点睛】学会把题目变形,解此方程主要依据等式两边同时加或减相同的数,等式仍然成立。
10. 黑兔 4x-x=360 480
【分析】列方程时,根据数量关系,一般把1倍的量设为未知数,等量关系为白兔数量-黑兔数量=360,据此解答。
【详解】白兔是黑兔的4倍,黑兔比白兔少360只,列方程解答时,可设黑兔为x只,列方程为4x-x=360,3x=360,x=120,白兔:4x=120×4=480,解得白兔有480只。
【点睛】列方程的关键是找出等量关系,解方程主要是依据等式的性质,等式两边同时乘或除同一个不为0的数,等式仍然成立;等式两边同时加或减相同的数,等式仍然成立。
11.x=4.8
【分析】平行四边形的面积=底×高。图中10米和x米、8米和6米是两组对应的底和高,则这两组数的乘积相等,据此列方程解答。
【详解】解:10x=8×6
10x=48
x=4.8
12.杨树有36棵;松树有24棵
【分析】根据题意,设松树有x棵,则杨树有1.5x棵,杨树与松树一共有60棵,列方程:x+1.5x=60,解方程,即可解答。
【详解】解:设松树有x棵,则杨树有1.5x棵
x+1.5x=60
2.5x=60
x=60÷2.5
x=24
杨树有:2.4×15=36(棵)
答:杨树有36棵,松树有24棵。
【点睛】本题考查方程的实际应用,根据题意,找出相关的量,列方程,解方程。
13.23.64千米
【分析】本题用方程解答比较简便。设地铁2号线长为x米,则1号线长为1.2x千米。根据1号线的长度+2号线的长度=52,据此列方程解答。
【详解】解:设地铁2号线长为x米,则1号线长为1.2x千米。
2.2x=52
答:太原市地铁2号线约长23.64千米。
【点睛】列方程解含有两个未知数的问题时,设其中的一个未知数是x,用含有x的式子表示另一个未知数,再根据等量关系即可列出方程。
14.73米
【分析】设乙队每天修x米,等量关系为:甲队、乙队每天修路的差×天数=120米,据此列方程解答。
【详解】解:设乙队每天修x米。
(x-65)×15=120
x-65=8
x=73
答:乙队每天修73米。
【点睛】列方程是解答应用题的一种有效的方法,解题的关键是弄清题意,找出应用题中的等量关系。
15.钢笔9元;练习本5元
【分析】设每本练习本x元,则每支钢笔(x+4)元,根据总价=单价×数量,分别求出钢笔和练习本花的钱数,相加等于66元,列方程解答即可。
【详解】解:设每本练习本x元,则每支钢笔(x+4)元。
6x+4(x+4)=66
6x+4x+16=66
10x=50
x=5
x+4=5+4=9
答:每支钢笔9元,每本练习本5元。
【点睛】此题考查了列方程解决实际问题,分别用未知数表示出两个量,找出等量关系解答即可。
16.20千米
【分析】根据速度和×相遇时间=两地之间的路程,设乙车每小时行驶x千米,则甲车每小时行驶1.25x千米,据此列方程解答即可。
【详解】解:设乙每小时行驶x千米,那么甲每小时行驶1.25x千米。
4(x+1.25x)=720
4×2.25x=720
x=80
1.25x=80×1.25=100(千米/时)
100-80=20(千米/时)
答:甲车每小时比乙车多行20千米。
【点睛】此题考查的目的是理解列方程解决问题的方法及应用,关键是找出等量关系,设出未知数,列方程解决问题。
