数学人教A版(2019)选择性必修第三册7.4.2超几何分布(共14张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.4.2超几何分布(共14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-18 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
7.4.2 超几何分布
情境引入
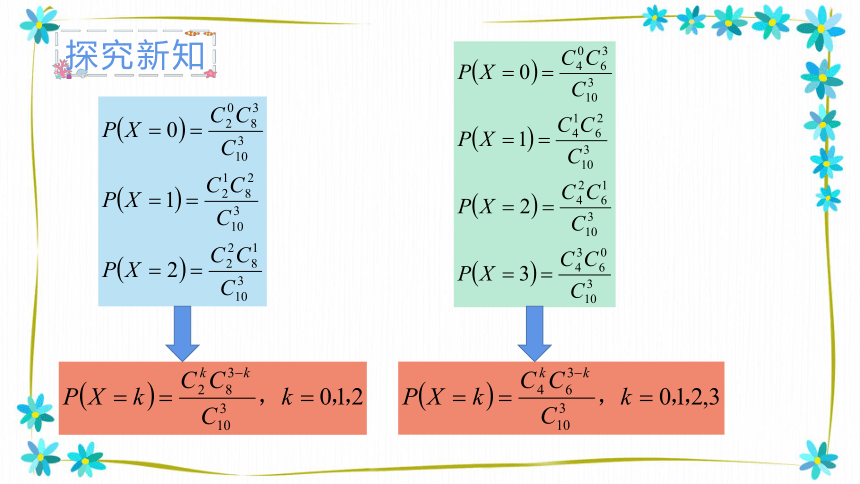
已知10件产品中有2件次品,分别采用有放回和不放回的方式随机抽取3件. 设抽取的3件产品中次品数为X,求随机变量X的分布列.
解:由题意可知,X可能的取值为0, 1, 2.
有
放
回
不
放
回
二项分布
【变式】已知10件产品中有4件次品,分别采用有放回和不放回的方式随机抽取3件. 设抽取的3件产品中次品数为X,求随机变量X的分布列.
解:由题意可知,X可能的取值为0, 1, 2,3.
有
放
回
不
放
回
二项分布
探究新知
一般地, 假设一批产品共有N件, 其中有M件次品. 从N件产品中随机抽取n件(不放回), 用X表示抽取的n件产品中的次品数, 则X的分布列为
超几何分布:
其中n, N, M∈N*, M≤N, n≤N, m=max{0, n-N+M}, r=min{n, M}. 如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布.
概念形成
注意:(1) “由较明显的两部分组成”: 如“男生、女生”, “正品、次品”;
(2) 注意分布列的表达式中,各个字母的含义及随机变量的取值范围.
N—总体中的个体总数
M—总体中的特殊个体总数
(如次品总数)
n—样本容量
k—样本中的特殊个体数
(如次品数)
概念辨析
1.思维辨析(对的打“√”,错的打“×”)
(1)将一枚硬币连抛3次,正面向上的次数X服从超几何分布.( )
(2)盒中有4个白球和3个黑球,无放回地摸取3个球,黑球的个数X服从超几何分布.( )
(3)某射手的命中率为0.8,现对目标射击3次,命中目标的次数X服从超几何分布.( )
×
√
×
2.在10个村庄中,有4个村庄交通不方便,若用随机变量X表示任选6个村庄中交通
不方便的村庄的个数,则X服从超几何分布,其参数为( )
A.N=10,M=4,n=6 B.N=10,M=6,n=4
C.N=14,M=10,n=4 D.N=14,M=4,n=10
A
D
例1.从6名男生和4名女生中任选4人参加演讲比赛,设
随机变量X表示所选4人中男生的人数.求X的分布列.
典例分析
解:依题意随机变量X服从超几何分布,X可能取0,1,2,3,4
∴随机变量X的分布列为
X 0 1 2 3 4
P
巩固应用
1、某乒乓球队9名队员,其中2名是种子选手,现挑选5名队员参加比赛,设X表示其中种子选手人数,求X的分布列。
巩固应用
课堂小结
你收获了什么?
思考题:某地工商局从某肉制品公司的一批数量较大的火腿肠产品中抽取10件产品,检验发现其中有3件产品的大肠菌群超标.
(1)如果在上述抽取的10件产品中任取2件,设随机变量ξ为大肠菌群超标的产品数量,求随机变量ξ的分布列及均值;
(2)如以该次检查的结果作为该批次每件产品大肠菌群超标的概率,如从该批次产品中任取2件,设随机变量η为大肠菌群超标的产品数量,求P(η=1)的值及随机变量η的均值.
7.4.2 超几何分布
情境引入
已知10件产品中有2件次品,分别采用有放回和不放回的方式随机抽取3件. 设抽取的3件产品中次品数为X,求随机变量X的分布列.
解:由题意可知,X可能的取值为0, 1, 2.
有
放
回
不
放
回
二项分布
【变式】已知10件产品中有4件次品,分别采用有放回和不放回的方式随机抽取3件. 设抽取的3件产品中次品数为X,求随机变量X的分布列.
解:由题意可知,X可能的取值为0, 1, 2,3.
有
放
回
不
放
回
二项分布
探究新知
一般地, 假设一批产品共有N件, 其中有M件次品. 从N件产品中随机抽取n件(不放回), 用X表示抽取的n件产品中的次品数, 则X的分布列为
超几何分布:
其中n, N, M∈N*, M≤N, n≤N, m=max{0, n-N+M}, r=min{n, M}. 如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布.
概念形成
注意:(1) “由较明显的两部分组成”: 如“男生、女生”, “正品、次品”;
(2) 注意分布列的表达式中,各个字母的含义及随机变量的取值范围.
N—总体中的个体总数
M—总体中的特殊个体总数
(如次品总数)
n—样本容量
k—样本中的特殊个体数
(如次品数)
概念辨析
1.思维辨析(对的打“√”,错的打“×”)
(1)将一枚硬币连抛3次,正面向上的次数X服从超几何分布.( )
(2)盒中有4个白球和3个黑球,无放回地摸取3个球,黑球的个数X服从超几何分布.( )
(3)某射手的命中率为0.8,现对目标射击3次,命中目标的次数X服从超几何分布.( )
×
√
×
2.在10个村庄中,有4个村庄交通不方便,若用随机变量X表示任选6个村庄中交通
不方便的村庄的个数,则X服从超几何分布,其参数为( )
A.N=10,M=4,n=6 B.N=10,M=6,n=4
C.N=14,M=10,n=4 D.N=14,M=4,n=10
A
D
例1.从6名男生和4名女生中任选4人参加演讲比赛,设
随机变量X表示所选4人中男生的人数.求X的分布列.
典例分析
解:依题意随机变量X服从超几何分布,X可能取0,1,2,3,4
∴随机变量X的分布列为
X 0 1 2 3 4
P
巩固应用
1、某乒乓球队9名队员,其中2名是种子选手,现挑选5名队员参加比赛,设X表示其中种子选手人数,求X的分布列。
巩固应用
课堂小结
你收获了什么?
思考题:某地工商局从某肉制品公司的一批数量较大的火腿肠产品中抽取10件产品,检验发现其中有3件产品的大肠菌群超标.
(1)如果在上述抽取的10件产品中任取2件,设随机变量ξ为大肠菌群超标的产品数量,求随机变量ξ的分布列及均值;
(2)如以该次检查的结果作为该批次每件产品大肠菌群超标的概率,如从该批次产品中任取2件,设随机变量η为大肠菌群超标的产品数量,求P(η=1)的值及随机变量η的均值.
