3.5 确定圆的条件 提升练习(无答案) 2022-2023学年北师大版九年级数学下册
文档属性
| 名称 | 3.5 确定圆的条件 提升练习(无答案) 2022-2023学年北师大版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 292.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 19:58:41 | ||
图片预览

文档简介
3.5 确定圆的条件(提升练习)-北师大版九年级下册
一.选择题
1.如图所示,△ABC的三个顶点的坐标分别为A(﹣1,3)、B(﹣2,﹣2)(4,﹣2),则△ABC外接圆半径的长为( )
A. B. C. D.
2.下列说法正确的是( )
A.长度相等的弧是等弧 B.直径是圆中最长的弦
C.弧是半圆 D.三点确定一个圆
3.下列条件中,能确定一个圆的是( )
A.经过已知点M
B.以点O为圆心,10cm长为半径
C.以10cm长为半径
D.以点O为圆心
4.如图,△ABC内接于⊙O,CD是⊙O的直径,则∠B=( )
A.44° B.34° C.50 D.46°
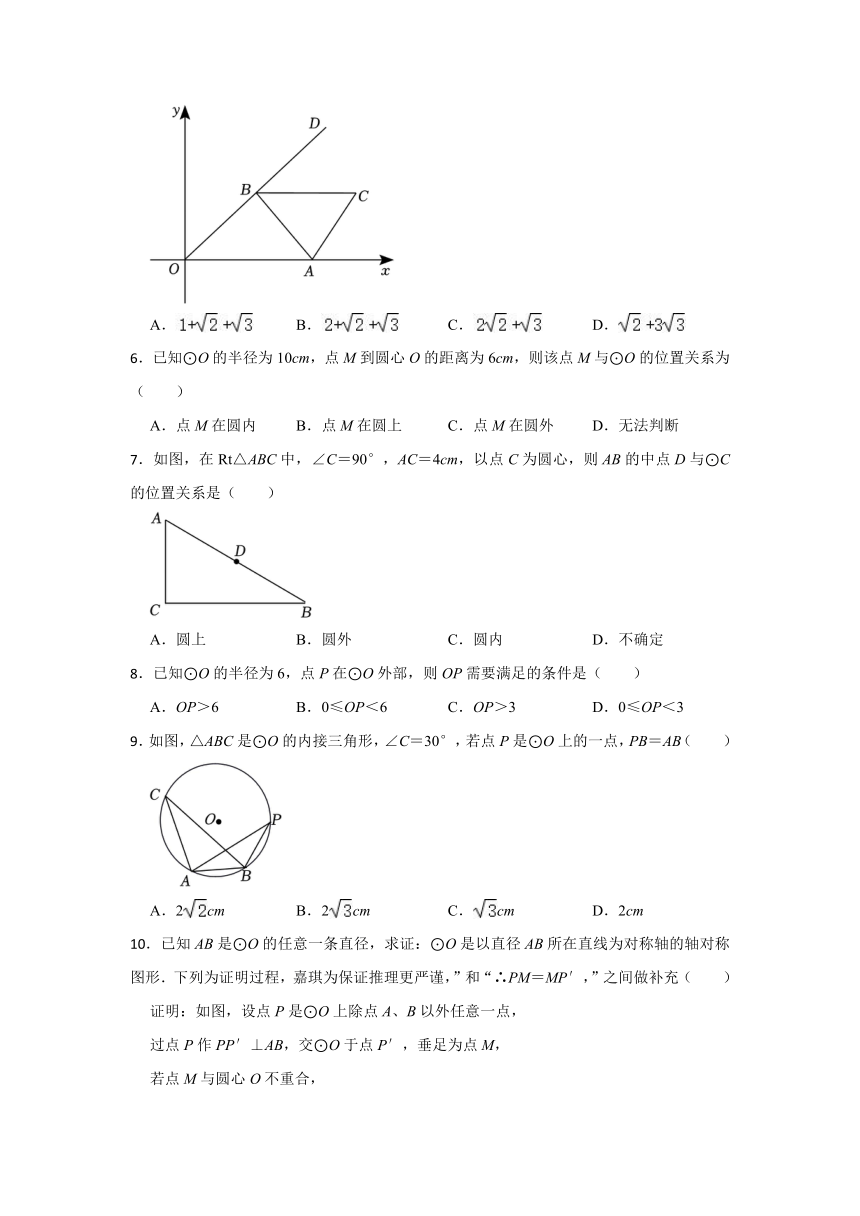
.如图,边长为2的等边△ABC的顶点A在x轴正半轴上移动,顶点B在直线y=x第一象限的分支上移动( )
A. B. C. D.
.已知⊙O的半径为10cm,点M到圆心O的距离为6cm,则该点M与⊙O的位置关系为( )
A.点M在圆内 B.点M在圆上 C.点M在圆外 D.无法判断
.如图,在Rt△ABC中,∠C=90°,AC=4cm,以点C为圆心,则AB的中点D与⊙C的位置关系是( )
A.圆上 B.圆外 C.圆内 D.不确定
.已知⊙O的半径为6,点P在⊙O外部,则OP需要满足的条件是( )
A.OP>6 B.0≤OP<6 C.OP>3 D.0≤OP<3
.如图,△ABC是⊙O的内接三角形,∠C=30°,若点P是⊙O上的一点,PB=AB( )
A.2cm B.2cm C.cm D.2cm
.已知AB是⊙O的任意一条直径,求证:⊙O是以直径AB所在直线为对称轴的轴对称图形.下列为证明过程,嘉琪为保证推理更严谨,”和“∴PM=MP′,”之间做补充( )
证明:如图,设点P是⊙O上除点A、B以外任意一点,
过点P作PP′⊥AB,交⊙O于点P′,垂足为点M,
若点M与圆心O不重合,
连接OP,OP′,在△OPP′中,∴PM=MP′,则AB是PP′的垂直平分线,
若点M与圆心O重合,显然AB是PP′的垂直平分线,
∴对于圆上任意一点P,在圆上都有关于直线AB的对称点P′
∴⊙O是以直径AB所在直线为对称轴的轴对称图形.
A.推理严谨,不必补充
B.应补充:∴△OPP′是等腰三角形
C.应补充:又∵PP′⊥AB
D.应补充:∴△OPP′是等腰三角形,又∵PP′⊥AB
二.填空题
.如图,在平面直角坐标系中,A(0,﹣3),B(2,﹣1),C(2,3).则△ABC的外心坐标为 .
.如图等边△ABC内接于⊙O,若⊙O的半径为1,则阴影部分的面积为 .
.如图,已知AB是⊙O的直径,点C在圆上 ,以点A为一个端点的优弧有 .
.如图,在△ABC中,BC=6,则△ABC面积的最大值为 .
.如图,⊙O为等边△ABC的外接圆,半径为2(不与点A,B重合),连接DA,DB
①当点D在劣弧中点时,四边形ADBC的面积是 ;
②四边形ADBC的面积y关于线段DC的长x的函数关系式为 .
三.解答题
.如图,△ABC的三个顶点在⊙O上,⊙O的半径为5,求弦BC的长.
.如图,△ABC内接于⊙O,高AD经过圆心O.
(1)求证:AB=AC;
(2)若BC=16,⊙O的半径为10.求△ABC的面积.
.如图,△ABC是⊙O的内接三角形,直径AB=4,交AB于点E,连接AD、BD.
(1)若∠CAB=25°,求∠AED的度数;
(2)求AD的长.
.如图,已知△ABC内接于⊙O,AB为⊙O的直径,,E为CA延长线上一点.
(1)连AD,求证:AD平分∠BAE;
(2)过点D作DF⊥AB于点F,求证:FA+AC=FB.
.如图,BD,CE是△ABC的高,CE相交于点F,M是BC的中点
(1)点B,C,D,E是否在以点M为圆心的同一个圆上?请说明理由.
(2)若AB=8,CF=6,求△ABC外接圆的半径长.
一.选择题
1.如图所示,△ABC的三个顶点的坐标分别为A(﹣1,3)、B(﹣2,﹣2)(4,﹣2),则△ABC外接圆半径的长为( )
A. B. C. D.
2.下列说法正确的是( )
A.长度相等的弧是等弧 B.直径是圆中最长的弦
C.弧是半圆 D.三点确定一个圆
3.下列条件中,能确定一个圆的是( )
A.经过已知点M
B.以点O为圆心,10cm长为半径
C.以10cm长为半径
D.以点O为圆心
4.如图,△ABC内接于⊙O,CD是⊙O的直径,则∠B=( )
A.44° B.34° C.50 D.46°
.如图,边长为2的等边△ABC的顶点A在x轴正半轴上移动,顶点B在直线y=x第一象限的分支上移动( )
A. B. C. D.
.已知⊙O的半径为10cm,点M到圆心O的距离为6cm,则该点M与⊙O的位置关系为( )
A.点M在圆内 B.点M在圆上 C.点M在圆外 D.无法判断
.如图,在Rt△ABC中,∠C=90°,AC=4cm,以点C为圆心,则AB的中点D与⊙C的位置关系是( )
A.圆上 B.圆外 C.圆内 D.不确定
.已知⊙O的半径为6,点P在⊙O外部,则OP需要满足的条件是( )
A.OP>6 B.0≤OP<6 C.OP>3 D.0≤OP<3
.如图,△ABC是⊙O的内接三角形,∠C=30°,若点P是⊙O上的一点,PB=AB( )
A.2cm B.2cm C.cm D.2cm
.已知AB是⊙O的任意一条直径,求证:⊙O是以直径AB所在直线为对称轴的轴对称图形.下列为证明过程,嘉琪为保证推理更严谨,”和“∴PM=MP′,”之间做补充( )
证明:如图,设点P是⊙O上除点A、B以外任意一点,
过点P作PP′⊥AB,交⊙O于点P′,垂足为点M,
若点M与圆心O不重合,
连接OP,OP′,在△OPP′中,∴PM=MP′,则AB是PP′的垂直平分线,
若点M与圆心O重合,显然AB是PP′的垂直平分线,
∴对于圆上任意一点P,在圆上都有关于直线AB的对称点P′
∴⊙O是以直径AB所在直线为对称轴的轴对称图形.
A.推理严谨,不必补充
B.应补充:∴△OPP′是等腰三角形
C.应补充:又∵PP′⊥AB
D.应补充:∴△OPP′是等腰三角形,又∵PP′⊥AB
二.填空题
.如图,在平面直角坐标系中,A(0,﹣3),B(2,﹣1),C(2,3).则△ABC的外心坐标为 .
.如图等边△ABC内接于⊙O,若⊙O的半径为1,则阴影部分的面积为 .
.如图,已知AB是⊙O的直径,点C在圆上 ,以点A为一个端点的优弧有 .
.如图,在△ABC中,BC=6,则△ABC面积的最大值为 .
.如图,⊙O为等边△ABC的外接圆,半径为2(不与点A,B重合),连接DA,DB
①当点D在劣弧中点时,四边形ADBC的面积是 ;
②四边形ADBC的面积y关于线段DC的长x的函数关系式为 .
三.解答题
.如图,△ABC的三个顶点在⊙O上,⊙O的半径为5,求弦BC的长.
.如图,△ABC内接于⊙O,高AD经过圆心O.
(1)求证:AB=AC;
(2)若BC=16,⊙O的半径为10.求△ABC的面积.
.如图,△ABC是⊙O的内接三角形,直径AB=4,交AB于点E,连接AD、BD.
(1)若∠CAB=25°,求∠AED的度数;
(2)求AD的长.
.如图,已知△ABC内接于⊙O,AB为⊙O的直径,,E为CA延长线上一点.
(1)连AD,求证:AD平分∠BAE;
(2)过点D作DF⊥AB于点F,求证:FA+AC=FB.
.如图,BD,CE是△ABC的高,CE相交于点F,M是BC的中点
(1)点B,C,D,E是否在以点M为圆心的同一个圆上?请说明理由.
(2)若AB=8,CF=6,求△ABC外接圆的半径长.
