5.1向量的概念及表示[下学期]
图片预览





文档简介
课件20张PPT。猫以5m/s的速度追赶一只以2m/s逃跑的小老鼠……问
题
情
境
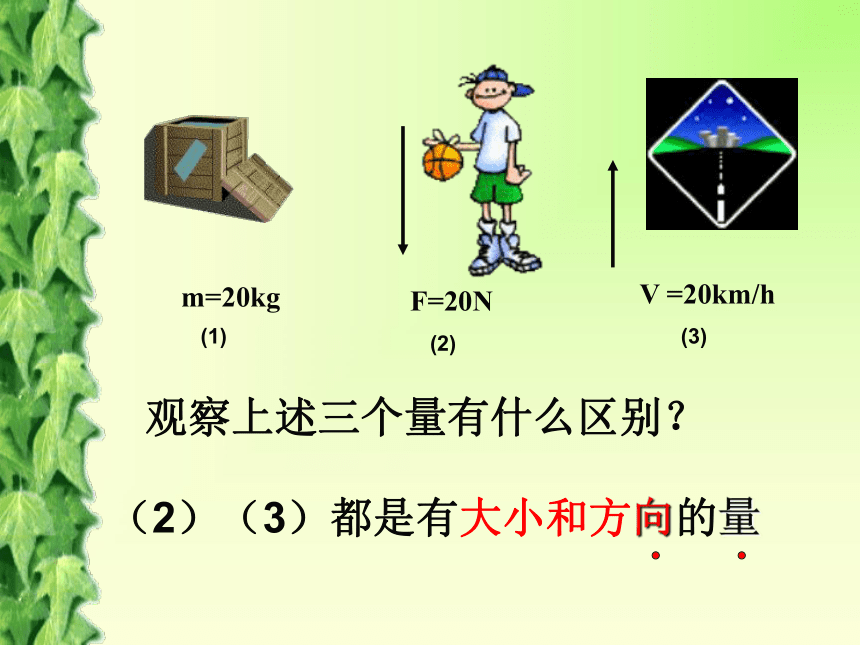
:F=20NV =20km/h (2)(3)都是有大小和方向的量m=20kg(1)(2)(3)观察上述三个量有什么区别?向量的概念及表示教学目标:(一)能力目标: 通过自学培养学生发现问题和提出问题,
学会分析问题和创造地解决问题的能力;(二)情感目标: 激发学生学习数学的兴趣和积极性,陶冶学生的
情操;培养学生追求质疑、求实的科学的精神。学习目标:1.向量的定义:
2.向量的表示方法:
3.向量的大小又称为:
符号记作:
4.两个特殊向量:
零向量:
单位向量:
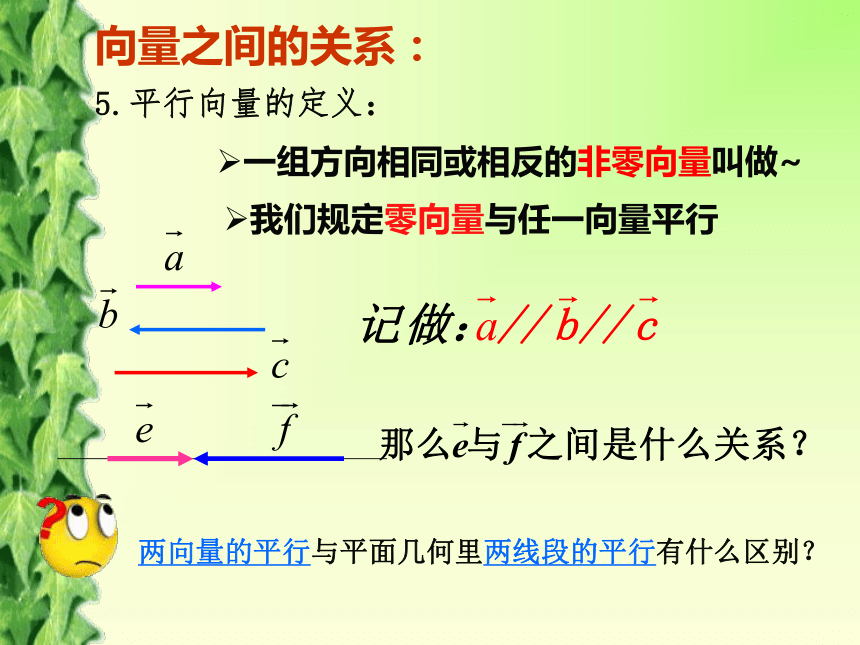
5.平行向量的定义:
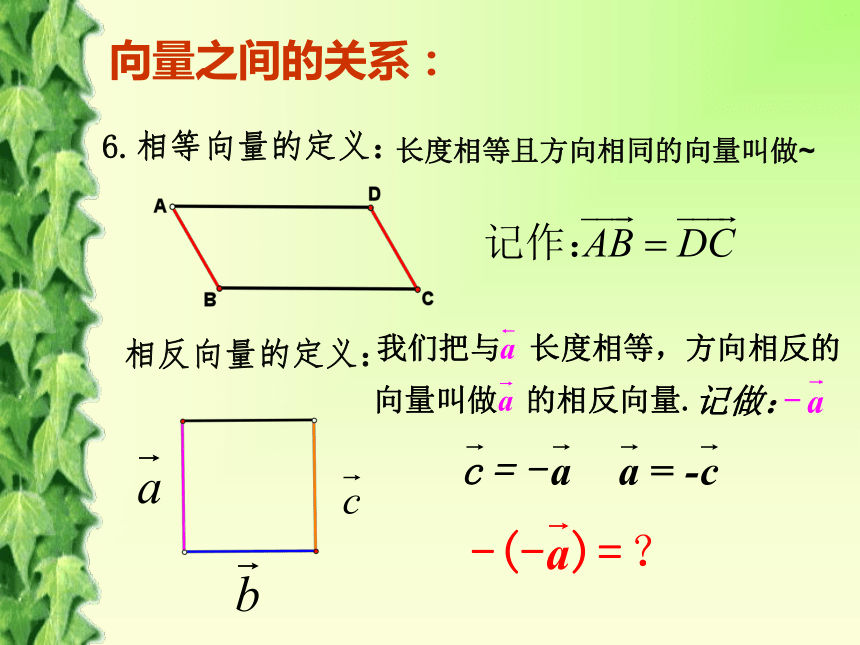
6.相等向量的定义
相反向量的定义:
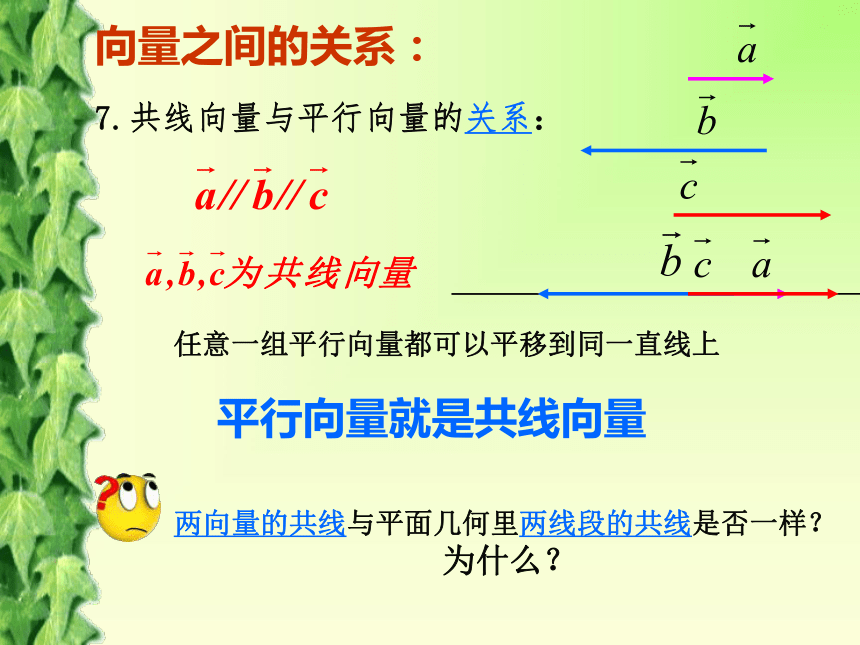
7.共线向量与平行向量的关系:向量的概念及表示:1.向量的定义:
2.向量的表示方法:
3.向量的大小:
记作:
4.两个特殊向量:
零向量:
单位向量:既有大小又有方向的量称为向量.(或称为 模 )指向量的长度长度为0的向量称为~长度等于1个单位长度的向量,叫做~记作:1)几何表示;
2)代数表示;向量之间的关系:5.平行向量的定义:一组方向相同或相反的非零向量叫做~我们规定零向量与任一向量平行两向量的平行与平面几何里两线段的平行有什么区别?6.相等向量的定义:长度相等且方向相同的向量叫做~相反向量的定义:向量之间的关系:任意一组平行向量都可以平移到同一直线上向量之间的关系:7.共线向量与平行向量的关系:平行向量就是共线向量两向量的共线与平面几何里两线段的共线是否一样?
为什么?例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:解:概念辨析:×××××√×√ 合作探究:练习:1.向量的定义:
2.向量的表示方法:
3.向量的大小又称为:
4.两个特殊向量:
零向量:
单位向量:
5.平行向量的定义:
6.相等向量的定义
相反向量的定义:
7.共线向量与平行向量的关系:小 结:课后作业:研究作业:(1)
用有向线段表示;(2)
i)用有向线段的起点与终点字母来表示;ii)用小写的字母来表示;A(起点)B(终点)上述向量还可表示为:有向线段的长度表示向量的大小注意:起点一定要写在终点的前面几何表示:代数表示:箭头所指的方向表示向量的方向两个特殊向量:2、单位向量:长度为 1 个单位长度的向量。零向量大小为0,方向不确定的.可以是任意方向.1单位向量大小为1,方向不一定相同。所以零向量只有一个,而单位向量可以有无数个思考:平面直角坐标系内,起点在原点的单位向量,
它们的终点的轨迹是什么图形?有向线段:规定了方向(即规定了起点和终点)的线段称为~通常在有向线段的终点处画上箭头表示它的方向.A(起点)B(终点)如图:AB叫有向线段 我们现在所研究的向量,与起点位置无关.
所以数学中的向量也叫 自由向量用有向线段表示向量时,起点可以取任意位置。
题
情
境
:F=20NV =20km/h (2)(3)都是有大小和方向的量m=20kg(1)(2)(3)观察上述三个量有什么区别?向量的概念及表示教学目标:(一)能力目标: 通过自学培养学生发现问题和提出问题,
学会分析问题和创造地解决问题的能力;(二)情感目标: 激发学生学习数学的兴趣和积极性,陶冶学生的
情操;培养学生追求质疑、求实的科学的精神。学习目标:1.向量的定义:
2.向量的表示方法:
3.向量的大小又称为:
符号记作:
4.两个特殊向量:
零向量:
单位向量:
5.平行向量的定义:
6.相等向量的定义
相反向量的定义:
7.共线向量与平行向量的关系:向量的概念及表示:1.向量的定义:
2.向量的表示方法:
3.向量的大小:
记作:
4.两个特殊向量:
零向量:
单位向量:既有大小又有方向的量称为向量.(或称为 模 )指向量的长度长度为0的向量称为~长度等于1个单位长度的向量,叫做~记作:1)几何表示;
2)代数表示;向量之间的关系:5.平行向量的定义:一组方向相同或相反的非零向量叫做~我们规定零向量与任一向量平行两向量的平行与平面几何里两线段的平行有什么区别?6.相等向量的定义:长度相等且方向相同的向量叫做~相反向量的定义:向量之间的关系:任意一组平行向量都可以平移到同一直线上向量之间的关系:7.共线向量与平行向量的关系:平行向量就是共线向量两向量的共线与平面几何里两线段的共线是否一样?
为什么?例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:解:概念辨析:×××××√×√ 合作探究:练习:1.向量的定义:
2.向量的表示方法:
3.向量的大小又称为:
4.两个特殊向量:
零向量:
单位向量:
5.平行向量的定义:
6.相等向量的定义
相反向量的定义:
7.共线向量与平行向量的关系:小 结:课后作业:研究作业:(1)
用有向线段表示;(2)
i)用有向线段的起点与终点字母来表示;ii)用小写的字母来表示;A(起点)B(终点)上述向量还可表示为:有向线段的长度表示向量的大小注意:起点一定要写在终点的前面几何表示:代数表示:箭头所指的方向表示向量的方向两个特殊向量:2、单位向量:长度为 1 个单位长度的向量。零向量大小为0,方向不确定的.可以是任意方向.1单位向量大小为1,方向不一定相同。所以零向量只有一个,而单位向量可以有无数个思考:平面直角坐标系内,起点在原点的单位向量,
它们的终点的轨迹是什么图形?有向线段:规定了方向(即规定了起点和终点)的线段称为~通常在有向线段的终点处画上箭头表示它的方向.A(起点)B(终点)如图:AB叫有向线段 我们现在所研究的向量,与起点位置无关.
所以数学中的向量也叫 自由向量用有向线段表示向量时,起点可以取任意位置。
