河南省周口市太康县2022-2023学年九年级上学期期末数学试题(含答案)
文档属性
| 名称 | 河南省周口市太康县2022-2023学年九年级上学期期末数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 217.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-18 00:00:00 | ||
图片预览


文档简介
2022-2023学年度上期期末考试
九年级数学试题
温馨提示:
1.本卷共6页,三大题,满分120分。请用黑色签字笔直接答在答题卡上。
2.答题前请先将姓名、准考证号填写清楚。
一、单选题(每小题3分,共30分)
1. 在函数 中,自变量的取值范围是()
A. B. C. D. 且
2. 下列说法(或做法)中正确的是()
A.明明的幸运数字是3,他抛出骰子时出3的机会比其它数字的机会大
B.妈妈买彩票没中过奖,她再买彩票中奖的机会一定比别人要大些
C.要知道抛一枚硬币正面朝上的机会,没有硬币可用啤酒瓶盖代替
D.在抛硬币实验中,婧婧认为一个一个地抛太慢,她用10枚硬币同时抛算作10次抛掷
3. 下面两个问题中都有两个变量:
①矩形的周长为20,矩形的面积与一边长;
②矩形的面积为20,矩形的宽与矩形的长.
其中变量与变量之间的函数关系表述正确的是()
A.①是反比例函数,②是二次函数
B.①是二次函数,②是反比例函数
C .①②都是二次函数
D.①②都是反比例函数
4. 如图,点P在△ABC的边AC上,要判断△BCP∽△ACB,需添加一个条件,其中不正确的是()
A.∠CBP=∠A B.∠CPB=∠CBA C. D.
5. 在三角形ABC中,C为直角,sinA=,则tanB的值为()
A. B. C. D.
6. 关于的一元二次方程 = 0,常数项为0, 则m值等于()
A. 1 B. 2 C. 1 或2 D. 0
7. 如图,在☉O 中,弦 AB, CD 相交于点 P, =45°,∠APD =80°, 则∠B的大小是()
A.35° B.45° C.60° D. 70°
第4题图 第7题图 第9题图
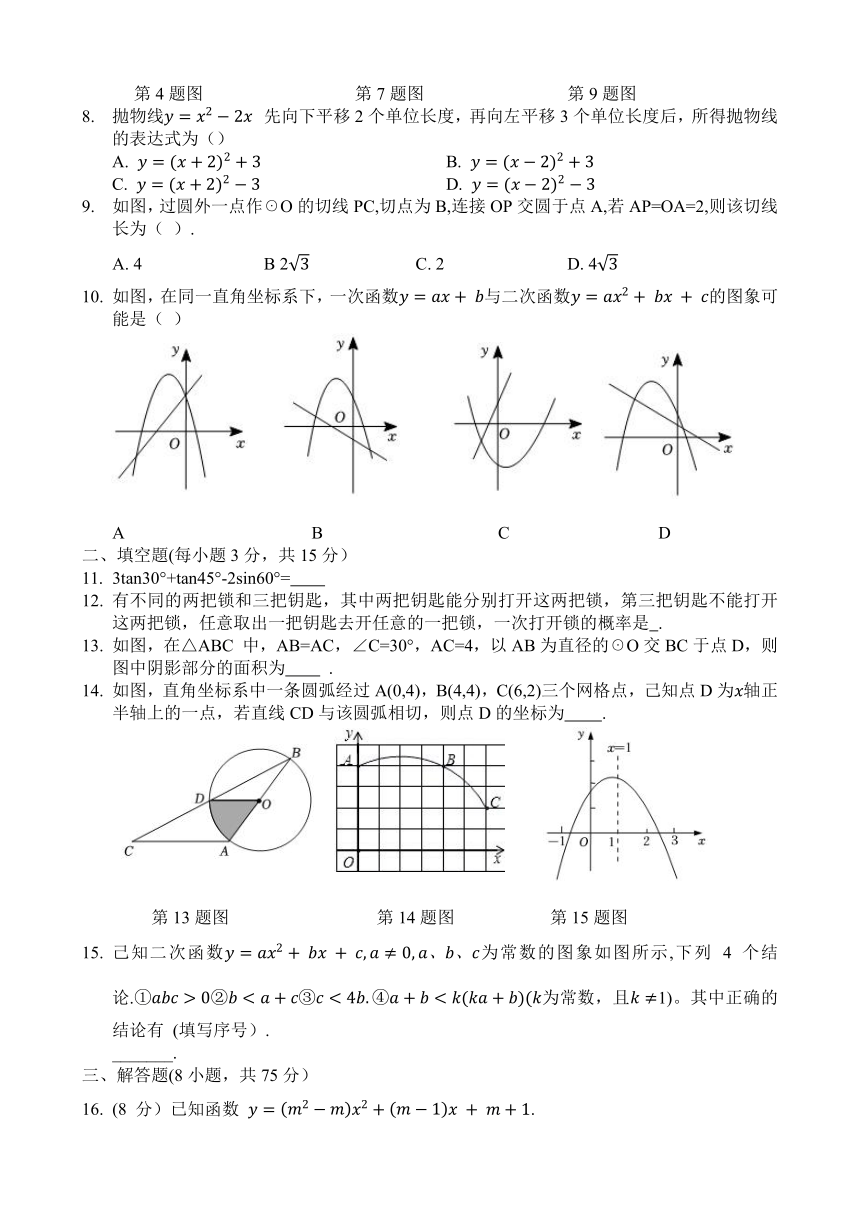
8. 拋物线 先向下平移2个单位长度,再向左平移3个单位长度后,所得抛物线的表达式为()
A. B.
C. D.
9. 如图,过圆外一点作☉O的切线PC,切点为B,连接OP交圆于点A,若AP=OA=2,则该切线长为( ).
A. 4 B 2 C. 2 D. 4
10. 如图,在同一直角坐标系下,一次函数与二次函数的图象可能是( )
A B C D
二、填空題(每小题3分,共15分)
11. 3tan30°+tan45°-2sin60°=
12. 有不同的两把锁和三把钥匙,其中两把钥匙能分别打开这两把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率是 .
13. 如图,在△ABC 中,AB=AC,∠C=30°,AC=4,以AB为直径的☉O交BC于点D,则图中阴影部分的面积为 .
14. 如图,直角坐标系中一条圆弧经过A(0,4),B(4,4),C(6,2)三个网格点,己知点D为轴正半轴上的一点,若直线CD与该圆弧相切,则点D的坐标为 .
第13题图 第14题图 第15题图
15. 己知二次函数为常数的图象如图所示,下列 4 个结论.为常数,且1)。其中正确的结论有 (填写序号).
_______.
三、解答题(8小题,共75分)
16. (8 分)已知函数 .
(1) 当为何值时,这个函数是关于的一次函数;
(2) 当为何值时,这个函数是关于的二次函数.
17. (9分)如图,D为☉O上一点,点C是直径延长线上的一点, 连接 CD,且 ∠CDA = ∠ CBD
⑴求证:CD是☉O的切线;
(2)若 DC=4,AC=2,求 OC 的长.
18. (9分)如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1) 任意闭合其中一个开关,则小灯泡发光的概率等于多少;
(2) 任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
19. (9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若坡角=30°,求大树的高度.(结果保留整数,参考数据:sin48°74, cos48°67 tan48° 1.73) 。
20. (1分)红灯笼,象征着国家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
⑴求甲、乙两种灯笼每对的进价;
(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对,若规定每对乙灯笼的利润不能高于30 元,设乙灯笼每对售价为元,小明一天通过乙灯笼获得利润元. ①求出与之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?
21. (9分)如图,已知是☉O的内接三角形,AD是☉O的直径, 连接BD.
(1) 若∠BAD=20°,求∠ACB的度数.
(2) 若BC平分∠ABD,AD=2,求AC的长.
22. (10分)【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明
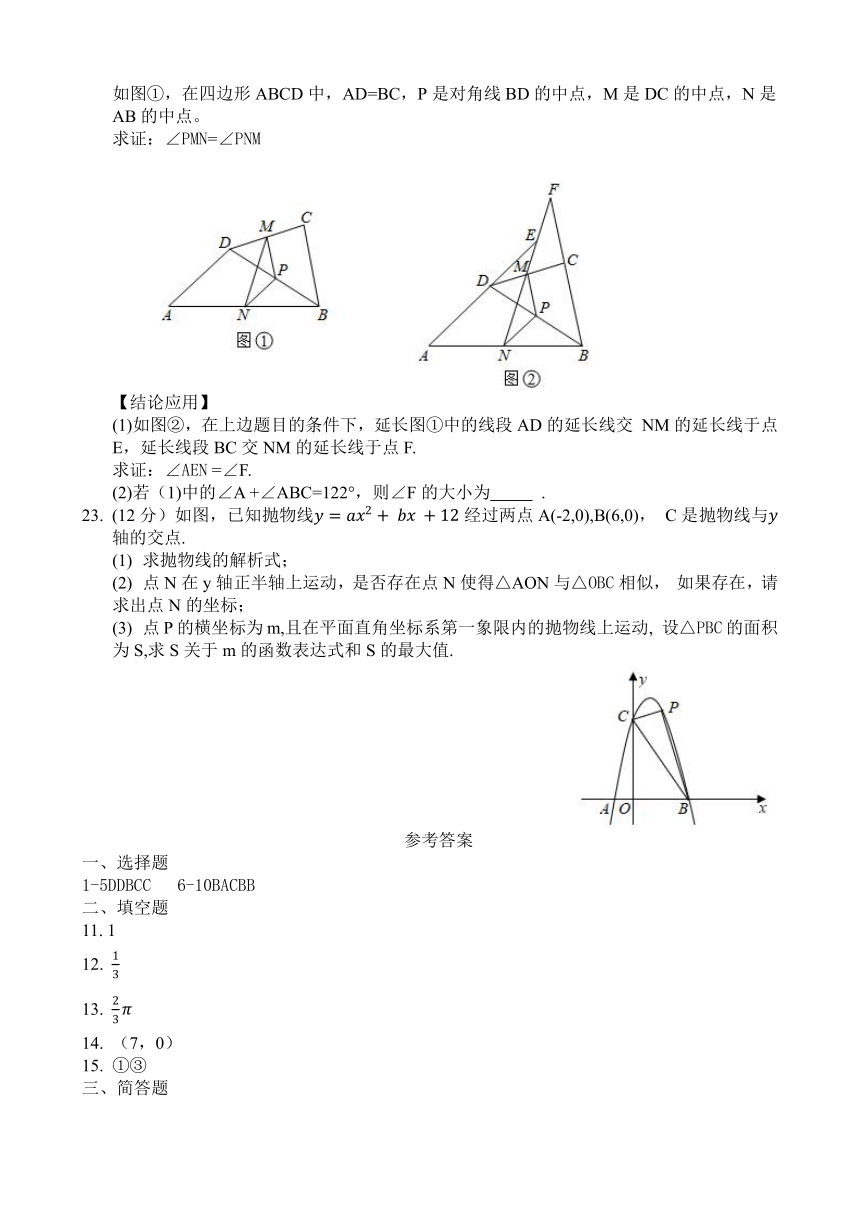
如图①,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点。
求证:∠PMN=∠PNM
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD的延长线交 NM的延长线于点E,延长线段BC交NM的延长线于点F.
求证:∠AEN =∠F.
(2)若(1)中的∠A +∠ABC=122°,则∠F的大小为 .
23. (12分)如图,已知抛物线经过两点A(-2,0),B(6,0), C是抛物线与轴的交点.
(1) 求抛物线的解析式;
(2) 点N在y轴正半轴上运动,是否存在点N使得△AON与△OBC相似, 如果存在,请求出点N的坐标;
(3) 点P的横坐标为m,且在平面直角坐标系第一象限内的抛物线上运动, 设△PBC的面积为S,求S关于m的函数表达式和S的最大值.
参考答案
选择题
1-5DDBCC 6-10BACBB
填空题
11. 1
12.
13.
14. (7,0)
15. ①③
简答题
16. 解:(1)依题意得:,
解得:m=0;
所以当m=0时,这个函数是关于的一次函数;
(2)依题意得≠0,
解得:m≠0且m≠1.
所以当m≠0和1时,这个函数是关于的二次函数.
17. 解:(1)如图,连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即∠ODB+∠ODA=90°,
∵OB=OD,
∴∠ABD=∠ODB,
又∵∠CDA=∠CBD,
∴∠ODA+∠CDA=90°,
即OD⊥CD,
∵OD是⊙O的半径,
∴CD是⊙O的切线;
(2)∵∠CDA=∠CBD,∠ACD=∠DCB,
∴△ACD∽△DCB,
∴,即,∴CB=8,
∴OA==3,
∴OC=OA+AC=3+2=5.
18. 解:(1)有4个开关,只有D开关一个闭合小灯发亮,
所以任意闭合其中一个开关,则小灯泡发光的概率是;
(2)画树状图如图:
结果任意闭合其中两个开关的情况共有12种,
其中能使小灯泡发光的情况有6种,
小灯泡发光的概率是.
19. 解:如图,过点D作DG⊥BC于G,DH⊥CE于H,
则四边形DHCG为矩形.
故DG=CH,CG=DH,DG∥HC,
∴∠DAH=∠FAE=30°,
在直角三角形AHD中,
∵∠DAH=30°,AD=6米,
∴DH=3(米),AH=3(米),
∴CG=3(米),
设BC为米,
在直角三角形ABC中,AC=,
∴DG=3+,BG=,
在直角三角形BDG中,∵BG=DG tan30°,
∴=(3+)
解得:x≈13,
∴大树的高度大约为13米
20. 解:(1)设甲种灯笼单价为x元/对,则乙种灯笼的单价为(+9)元/对,由题意得:
,解得=26,
经检验,=26是原方程的解,且符合题意,
∴+9=26+9=35,
答:甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对.
(2)①,
答:与之间的函数解析式为:
②∵=-2<0,
∴函数y有最大值,该二次函数的对称轴为:=57,
物价部门规定每对乙灯笼的不高于每对30元,
∴-35≤30,
∴≤65,
∵<57时,随的增大而增大,
∴当=57时,最大=9468.
答:乙种灯笼的销售单价为每对57元时,一天获得利润最大,最大利润是9468元
21. 解:(1)∵AD是⊙O的直径,
∴∠ABD=90°,
∵∠BAD=20°,
∴∠D=90°-20°=70°,
∴∠ACB=∠D=70°;
(2)连接OC,
∵BC平分∠ABD,
∴∠ABC=∠ABD=45°,
∴∠AOC=2∠ABC=90°,
∵AD=2,
∴AO=1,
∴AC=AO=.
22. 证明:∵P,M,N分别是BD,DC,AB中点,
∴PM=BC,PN=AD,
∵BC=AD,
∴PM=PN,
∴∠PMN=∠PNM.
(1)证明:∵P,M,N分别是BD,DC,AB中点,
∴PM∥BC,PN∥AD,
∴∠F=∠PMN,∠AEN=∠PNM,
∵∠PMN=∠PNM,
∴∠AEN=∠F.
(2)解:∵∠A+∠ANE+∠AEN=180°,
∠NBF+∠BNF+∠F=180°,
∴∠A+∠NBF+∠ANE+∠BNF+∠AEN+∠F=360°,
∴122°+180°+2∠F=360°,
∴∠F=29°.
故答案为:29°.
23. 解:(1)把A(-2,0),B(6,0)代入得:
,解得,
∴抛物线的解析式为;
(2)求C点坐标,
在△OBC中,OB=6,OC=12
△AON∽△OBC, 分两种情况
①当OA为直角三角形长边∵△AON∽△OBC
∴ 得
②当OA为直角三角形短边∵△AON∽△OBC,
∴ 得
∴N点坐标为(1,0)或(4,0)
(3)(2)过点P作PF∥y轴,交BC于点F,如图2所示.
由(2)知点C的坐标为(0,12).
设直线BC的解析式为,
将B(6,0)、C(0,12)代入,得
∵点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,
∴点P的坐标为(),则点F的坐标为(),
∴PF=-=- ,
∴S=PF OB=-3+18=-3,
∴当m=3时,△PBC面积取最大值,最大值为27
∵点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,
∴0<m<6.
综上所述,S关于m的函数表达式为S=-3+18(0<m<6),S的最大值27
九年级数学试题
温馨提示:
1.本卷共6页,三大题,满分120分。请用黑色签字笔直接答在答题卡上。
2.答题前请先将姓名、准考证号填写清楚。
一、单选题(每小题3分,共30分)
1. 在函数 中,自变量的取值范围是()
A. B. C. D. 且
2. 下列说法(或做法)中正确的是()
A.明明的幸运数字是3,他抛出骰子时出3的机会比其它数字的机会大
B.妈妈买彩票没中过奖,她再买彩票中奖的机会一定比别人要大些
C.要知道抛一枚硬币正面朝上的机会,没有硬币可用啤酒瓶盖代替
D.在抛硬币实验中,婧婧认为一个一个地抛太慢,她用10枚硬币同时抛算作10次抛掷
3. 下面两个问题中都有两个变量:
①矩形的周长为20,矩形的面积与一边长;
②矩形的面积为20,矩形的宽与矩形的长.
其中变量与变量之间的函数关系表述正确的是()
A.①是反比例函数,②是二次函数
B.①是二次函数,②是反比例函数
C .①②都是二次函数
D.①②都是反比例函数
4. 如图,点P在△ABC的边AC上,要判断△BCP∽△ACB,需添加一个条件,其中不正确的是()
A.∠CBP=∠A B.∠CPB=∠CBA C. D.
5. 在三角形ABC中,C为直角,sinA=,则tanB的值为()
A. B. C. D.
6. 关于的一元二次方程 = 0,常数项为0, 则m值等于()
A. 1 B. 2 C. 1 或2 D. 0
7. 如图,在☉O 中,弦 AB, CD 相交于点 P, =45°,∠APD =80°, 则∠B的大小是()
A.35° B.45° C.60° D. 70°
第4题图 第7题图 第9题图
8. 拋物线 先向下平移2个单位长度,再向左平移3个单位长度后,所得抛物线的表达式为()
A. B.
C. D.
9. 如图,过圆外一点作☉O的切线PC,切点为B,连接OP交圆于点A,若AP=OA=2,则该切线长为( ).
A. 4 B 2 C. 2 D. 4
10. 如图,在同一直角坐标系下,一次函数与二次函数的图象可能是( )
A B C D
二、填空題(每小题3分,共15分)
11. 3tan30°+tan45°-2sin60°=
12. 有不同的两把锁和三把钥匙,其中两把钥匙能分别打开这两把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率是 .
13. 如图,在△ABC 中,AB=AC,∠C=30°,AC=4,以AB为直径的☉O交BC于点D,则图中阴影部分的面积为 .
14. 如图,直角坐标系中一条圆弧经过A(0,4),B(4,4),C(6,2)三个网格点,己知点D为轴正半轴上的一点,若直线CD与该圆弧相切,则点D的坐标为 .
第13题图 第14题图 第15题图
15. 己知二次函数为常数的图象如图所示,下列 4 个结论.为常数,且1)。其中正确的结论有 (填写序号).
_______.
三、解答题(8小题,共75分)
16. (8 分)已知函数 .
(1) 当为何值时,这个函数是关于的一次函数;
(2) 当为何值时,这个函数是关于的二次函数.
17. (9分)如图,D为☉O上一点,点C是直径延长线上的一点, 连接 CD,且 ∠CDA = ∠ CBD
⑴求证:CD是☉O的切线;
(2)若 DC=4,AC=2,求 OC 的长.
18. (9分)如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1) 任意闭合其中一个开关,则小灯泡发光的概率等于多少;
(2) 任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
19. (9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若坡角=30°,求大树的高度.(结果保留整数,参考数据:sin48°74, cos48°67 tan48° 1.73) 。
20. (1分)红灯笼,象征着国家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
⑴求甲、乙两种灯笼每对的进价;
(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对,若规定每对乙灯笼的利润不能高于30 元,设乙灯笼每对售价为元,小明一天通过乙灯笼获得利润元. ①求出与之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?
21. (9分)如图,已知是☉O的内接三角形,AD是☉O的直径, 连接BD.
(1) 若∠BAD=20°,求∠ACB的度数.
(2) 若BC平分∠ABD,AD=2,求AC的长.
22. (10分)【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明
如图①,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点。
求证:∠PMN=∠PNM
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD的延长线交 NM的延长线于点E,延长线段BC交NM的延长线于点F.
求证:∠AEN =∠F.
(2)若(1)中的∠A +∠ABC=122°,则∠F的大小为 .
23. (12分)如图,已知抛物线经过两点A(-2,0),B(6,0), C是抛物线与轴的交点.
(1) 求抛物线的解析式;
(2) 点N在y轴正半轴上运动,是否存在点N使得△AON与△OBC相似, 如果存在,请求出点N的坐标;
(3) 点P的横坐标为m,且在平面直角坐标系第一象限内的抛物线上运动, 设△PBC的面积为S,求S关于m的函数表达式和S的最大值.
参考答案
选择题
1-5DDBCC 6-10BACBB
填空题
11. 1
12.
13.
14. (7,0)
15. ①③
简答题
16. 解:(1)依题意得:,
解得:m=0;
所以当m=0时,这个函数是关于的一次函数;
(2)依题意得≠0,
解得:m≠0且m≠1.
所以当m≠0和1时,这个函数是关于的二次函数.
17. 解:(1)如图,连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即∠ODB+∠ODA=90°,
∵OB=OD,
∴∠ABD=∠ODB,
又∵∠CDA=∠CBD,
∴∠ODA+∠CDA=90°,
即OD⊥CD,
∵OD是⊙O的半径,
∴CD是⊙O的切线;
(2)∵∠CDA=∠CBD,∠ACD=∠DCB,
∴△ACD∽△DCB,
∴,即,∴CB=8,
∴OA==3,
∴OC=OA+AC=3+2=5.
18. 解:(1)有4个开关,只有D开关一个闭合小灯发亮,
所以任意闭合其中一个开关,则小灯泡发光的概率是;
(2)画树状图如图:
结果任意闭合其中两个开关的情况共有12种,
其中能使小灯泡发光的情况有6种,
小灯泡发光的概率是.
19. 解:如图,过点D作DG⊥BC于G,DH⊥CE于H,
则四边形DHCG为矩形.
故DG=CH,CG=DH,DG∥HC,
∴∠DAH=∠FAE=30°,
在直角三角形AHD中,
∵∠DAH=30°,AD=6米,
∴DH=3(米),AH=3(米),
∴CG=3(米),
设BC为米,
在直角三角形ABC中,AC=,
∴DG=3+,BG=,
在直角三角形BDG中,∵BG=DG tan30°,
∴=(3+)
解得:x≈13,
∴大树的高度大约为13米
20. 解:(1)设甲种灯笼单价为x元/对,则乙种灯笼的单价为(+9)元/对,由题意得:
,解得=26,
经检验,=26是原方程的解,且符合题意,
∴+9=26+9=35,
答:甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对.
(2)①,
答:与之间的函数解析式为:
②∵=-2<0,
∴函数y有最大值,该二次函数的对称轴为:=57,
物价部门规定每对乙灯笼的不高于每对30元,
∴-35≤30,
∴≤65,
∵<57时,随的增大而增大,
∴当=57时,最大=9468.
答:乙种灯笼的销售单价为每对57元时,一天获得利润最大,最大利润是9468元
21. 解:(1)∵AD是⊙O的直径,
∴∠ABD=90°,
∵∠BAD=20°,
∴∠D=90°-20°=70°,
∴∠ACB=∠D=70°;
(2)连接OC,
∵BC平分∠ABD,
∴∠ABC=∠ABD=45°,
∴∠AOC=2∠ABC=90°,
∵AD=2,
∴AO=1,
∴AC=AO=.
22. 证明:∵P,M,N分别是BD,DC,AB中点,
∴PM=BC,PN=AD,
∵BC=AD,
∴PM=PN,
∴∠PMN=∠PNM.
(1)证明:∵P,M,N分别是BD,DC,AB中点,
∴PM∥BC,PN∥AD,
∴∠F=∠PMN,∠AEN=∠PNM,
∵∠PMN=∠PNM,
∴∠AEN=∠F.
(2)解:∵∠A+∠ANE+∠AEN=180°,
∠NBF+∠BNF+∠F=180°,
∴∠A+∠NBF+∠ANE+∠BNF+∠AEN+∠F=360°,
∴122°+180°+2∠F=360°,
∴∠F=29°.
故答案为:29°.
23. 解:(1)把A(-2,0),B(6,0)代入得:
,解得,
∴抛物线的解析式为;
(2)求C点坐标,
在△OBC中,OB=6,OC=12
△AON∽△OBC, 分两种情况
①当OA为直角三角形长边∵△AON∽△OBC
∴ 得
②当OA为直角三角形短边∵△AON∽△OBC,
∴ 得
∴N点坐标为(1,0)或(4,0)
(3)(2)过点P作PF∥y轴,交BC于点F,如图2所示.
由(2)知点C的坐标为(0,12).
设直线BC的解析式为,
将B(6,0)、C(0,12)代入,得
∵点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,
∴点P的坐标为(),则点F的坐标为(),
∴PF=-=- ,
∴S=PF OB=-3+18=-3,
∴当m=3时,△PBC面积取最大值,最大值为27
∵点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,
∴0<m<6.
综上所述,S关于m的函数表达式为S=-3+18(0<m<6),S的最大值27
同课章节目录
