17.2.2 函数的图象(1) 教案
图片预览


文档简介
中小学教育资源及组卷应用平台
17.2.2 函数的图象(1) 教学设计
课题 17.2.2 函数的图象(1) 单元 第17 单元 学科 数学 年级 八年级(下)
教材分析 使学生理解函数的图象是由许多点按照一定的规律组成的图形.能够在平面直角坐标系内画出简单函数的图象.
核心素养分析 结合实际问题,经历探索用图象表示函数的过程.通过学生自己动手,体会用描点法画函数的图象的步骤.培养学生用类比的方法探究新知识的能力.
学习目标 1.掌握用描点法画出一些简单函数的图象; 2.理解解析法和图象法表示函数关系的相互转换.
重点 用描点法画函数图象.
难点 灵活选择自变量的值,便于描点使画图简便.注意自变量的取值范围.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题在上节课我们学到,下图气温曲线图表示的是某日气温T(℃)与时间t(时)的函数关系,那么如何在直角坐标系中表示呢?归纳:1世纪教育网版权所有在上面的图形中,有一个直角坐标系,它的横轴表示 ;它的纵轴表示 ,这一气温曲线图实质上给出某日气温T(℃)与时间,(时)的函数关系,因为对于一日24小时的任何一刻,都有惟一的温度与之对应。例如,上午10时的气温是 ℃,表现在曲线上,就是可以找到这样的对应点,它的坐标 ,也就是说,当t=10时,对应的函数值T=2.由于坐标平面上的点与有序实数对是 的关系,因此,气温曲线图是由许许多多的点(t,T)组成的。从图中我们可以看出,随着时间 t(时)的变化,相应的气温 T(℃)也随之变化. 思考自议使学生理解函数的图象是由许多点按照一定的规律组成的图形. 结合实际问题,经历探索用图象表示函数的过程.
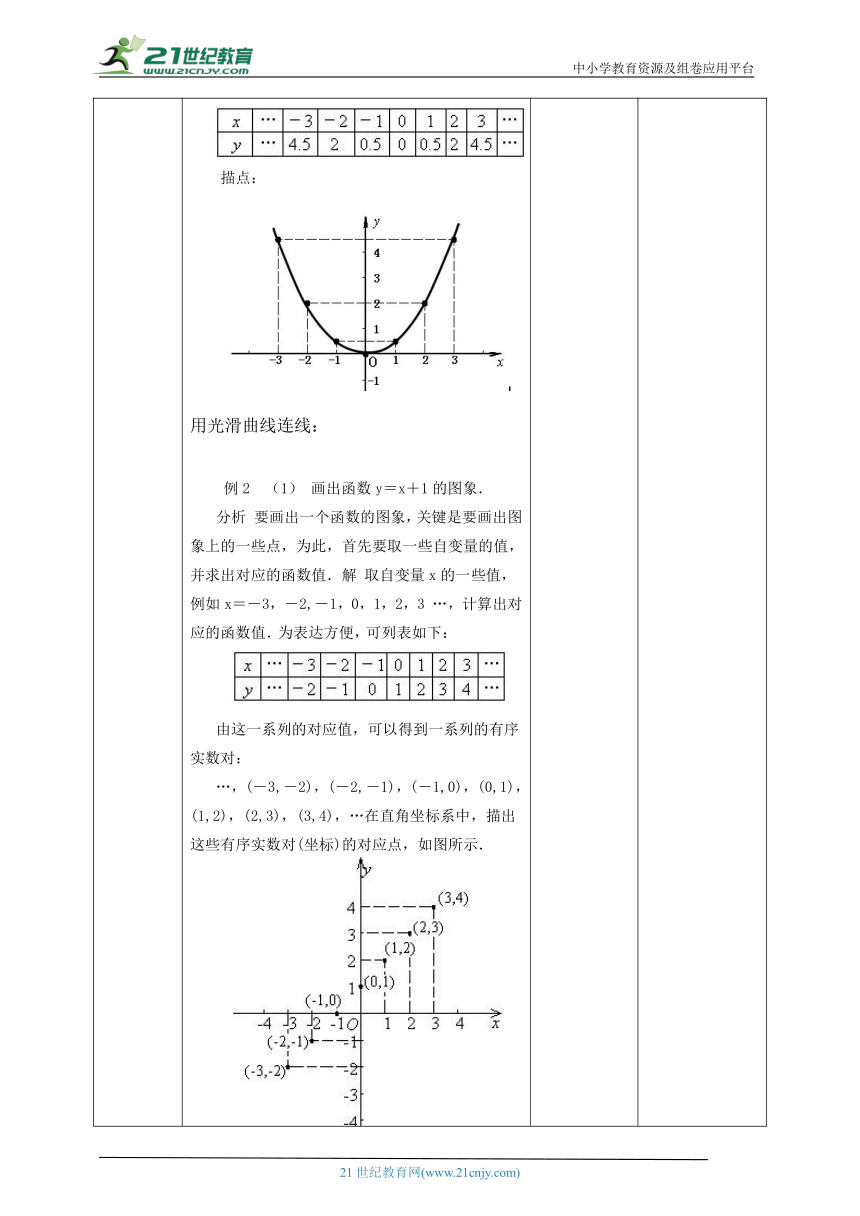
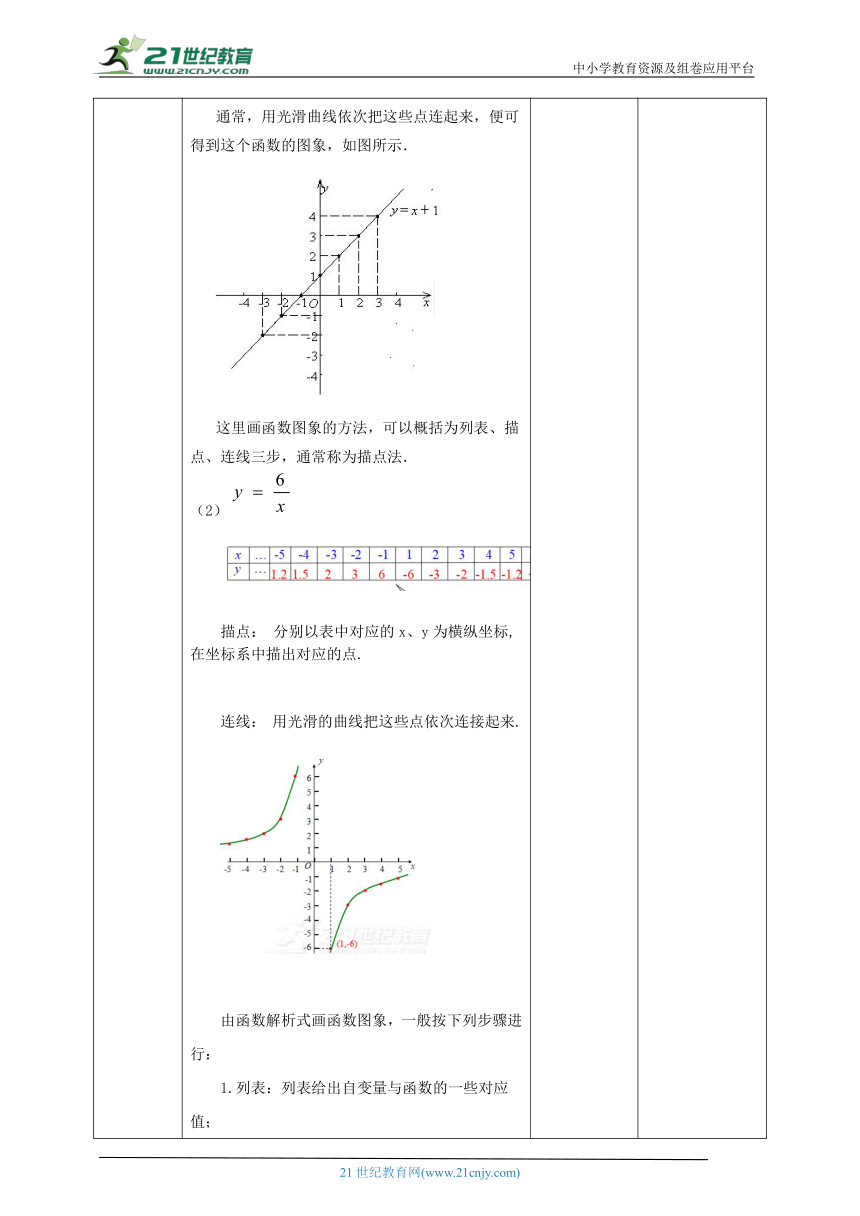
讲授新课 二、提炼概念函数的图象是由直角坐标系中的一系列点组成,图象上的每一点坐标(x,y)代表了函数的一对对应值,即把自变量x与函数y的每一对对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出相应的点,这些点组成的图形,就是这个函数的图象。1世纪教育网版权所有三、典例精讲例1 画出函数的图象.分析 要画出一个函数的图象,关键是要画 ( http: / / www.21cnjy.com )出图象上的一些点,为此,首先要取一些自变量的值,并求出对应的函数值.取自变量x的一些值,例如x=-3,-2,-1,0,1,2,3 …,计算出对应的函数值.由这一系列的对应值,可以得到一系列的有序实数对:…,(-3, ),(-2, ( http: / / www.21cnjy.com )),(-1, ),(0, ),(1, ),(2, ),(3, ),…在直角坐标系中,描出这些有序实数对(坐标)的对应点,如图所示.21教育网解 列表:描点:用光滑曲线连线: 例2 (1) 画出函数y=x+1的图象.分析 要画出一个函数的图象,关键是 ( http: / / www.21cnjy.com )要画出图象上的一些点,为此,首先要取一些自变量的值,并求出对应的函数值.解 取自变量x的一些值,例如x=-3,-2,-1,0,1,2,3 …,计算出对应的函数值.为表达方便,可列表如下:21··com由这一系列的对应值,可以得到一系列的有序实数对:…,(-3,-2),(-2,-1),(- ( http: / / www.21cnjy.com )1,0),(0,1),(1,2),(2,3),(3,4),…在直角坐标系中,描出这些有序实数对(坐标)的对应点,如图所示. ( http: / / www.21cnjy.com )通常,用光滑曲线依次把这些点连起来,便可得到这个函数的图象,如图所示.这里画函数图象的方法,可以概括为列表、描点、连线三步,通常称为描点法.(2)描点: 分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.连线: 用光滑的曲线把这些点依次连接起来.由函数解析式画函数图象,一般按下列步骤进行:1.列表:列表给出自变量与函数的一些对应值;2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.描出的点越多,图象越精确.有时不能把所有的点都描出,就用光滑的曲线连结画出的点,从而得到函数的近似的图象. 掌握用描点法画出一些简单函数的图象. 理解解析法和图象法表示函数关系的相互转换.
课堂练习 四、巩固训练 1.在所给的直角坐标系中画出函数的图象(先填写下表,再描点、连线). ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )解:2.画出函数的图象(先填写下表,再描点、然后用光滑曲线连结各点) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )解:3.在同一坐标系下画出下列函数的图象,并观察、判断两图象是什么形状的图形,它们的位置关系如何。(1)y=4x-1; (2)y=4x+1.xy=4x-1y=4x+1 ( http: / / www.21cnjy.com ) 4、如图等腰三角形的周长为12底为y,是腰为x的函数(1)写出函数关系式(2)求自变量取值范围(3)画出函数图像
课堂小结 课堂小结1. 什么是函数的图象 函数的图象是由直角坐标系中的一系列点组成.图象上每一点坐标(x,y)代表了函数的一对对应值,它的横坐标X表示自变量的某一个值,纵坐标y表示与它对应的函数值.2. 画函数图象的步骤是什么?
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
17.2.2 函数的图象(1) 教学设计
课题 17.2.2 函数的图象(1) 单元 第17 单元 学科 数学 年级 八年级(下)
教材分析 使学生理解函数的图象是由许多点按照一定的规律组成的图形.能够在平面直角坐标系内画出简单函数的图象.
核心素养分析 结合实际问题,经历探索用图象表示函数的过程.通过学生自己动手,体会用描点法画函数的图象的步骤.培养学生用类比的方法探究新知识的能力.
学习目标 1.掌握用描点法画出一些简单函数的图象; 2.理解解析法和图象法表示函数关系的相互转换.
重点 用描点法画函数图象.
难点 灵活选择自变量的值,便于描点使画图简便.注意自变量的取值范围.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题在上节课我们学到,下图气温曲线图表示的是某日气温T(℃)与时间t(时)的函数关系,那么如何在直角坐标系中表示呢?归纳:1世纪教育网版权所有在上面的图形中,有一个直角坐标系,它的横轴表示 ;它的纵轴表示 ,这一气温曲线图实质上给出某日气温T(℃)与时间,(时)的函数关系,因为对于一日24小时的任何一刻,都有惟一的温度与之对应。例如,上午10时的气温是 ℃,表现在曲线上,就是可以找到这样的对应点,它的坐标 ,也就是说,当t=10时,对应的函数值T=2.由于坐标平面上的点与有序实数对是 的关系,因此,气温曲线图是由许许多多的点(t,T)组成的。从图中我们可以看出,随着时间 t(时)的变化,相应的气温 T(℃)也随之变化. 思考自议使学生理解函数的图象是由许多点按照一定的规律组成的图形. 结合实际问题,经历探索用图象表示函数的过程.
讲授新课 二、提炼概念函数的图象是由直角坐标系中的一系列点组成,图象上的每一点坐标(x,y)代表了函数的一对对应值,即把自变量x与函数y的每一对对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出相应的点,这些点组成的图形,就是这个函数的图象。1世纪教育网版权所有三、典例精讲例1 画出函数的图象.分析 要画出一个函数的图象,关键是要画 ( http: / / www.21cnjy.com )出图象上的一些点,为此,首先要取一些自变量的值,并求出对应的函数值.取自变量x的一些值,例如x=-3,-2,-1,0,1,2,3 …,计算出对应的函数值.由这一系列的对应值,可以得到一系列的有序实数对:…,(-3, ),(-2, ( http: / / www.21cnjy.com )),(-1, ),(0, ),(1, ),(2, ),(3, ),…在直角坐标系中,描出这些有序实数对(坐标)的对应点,如图所示.21教育网解 列表:描点:用光滑曲线连线: 例2 (1) 画出函数y=x+1的图象.分析 要画出一个函数的图象,关键是 ( http: / / www.21cnjy.com )要画出图象上的一些点,为此,首先要取一些自变量的值,并求出对应的函数值.解 取自变量x的一些值,例如x=-3,-2,-1,0,1,2,3 …,计算出对应的函数值.为表达方便,可列表如下:21··com由这一系列的对应值,可以得到一系列的有序实数对:…,(-3,-2),(-2,-1),(- ( http: / / www.21cnjy.com )1,0),(0,1),(1,2),(2,3),(3,4),…在直角坐标系中,描出这些有序实数对(坐标)的对应点,如图所示. ( http: / / www.21cnjy.com )通常,用光滑曲线依次把这些点连起来,便可得到这个函数的图象,如图所示.这里画函数图象的方法,可以概括为列表、描点、连线三步,通常称为描点法.(2)描点: 分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.连线: 用光滑的曲线把这些点依次连接起来.由函数解析式画函数图象,一般按下列步骤进行:1.列表:列表给出自变量与函数的一些对应值;2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.描出的点越多,图象越精确.有时不能把所有的点都描出,就用光滑的曲线连结画出的点,从而得到函数的近似的图象. 掌握用描点法画出一些简单函数的图象. 理解解析法和图象法表示函数关系的相互转换.
课堂练习 四、巩固训练 1.在所给的直角坐标系中画出函数的图象(先填写下表,再描点、连线). ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )解:2.画出函数的图象(先填写下表,再描点、然后用光滑曲线连结各点) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )解:3.在同一坐标系下画出下列函数的图象,并观察、判断两图象是什么形状的图形,它们的位置关系如何。(1)y=4x-1; (2)y=4x+1.xy=4x-1y=4x+1 ( http: / / www.21cnjy.com ) 4、如图等腰三角形的周长为12底为y,是腰为x的函数(1)写出函数关系式(2)求自变量取值范围(3)画出函数图像
课堂小结 课堂小结1. 什么是函数的图象 函数的图象是由直角坐标系中的一系列点组成.图象上每一点坐标(x,y)代表了函数的一对对应值,它的横坐标X表示自变量的某一个值,纵坐标y表示与它对应的函数值.2. 画函数图象的步骤是什么?
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
