17.2.2 函数的图象(1) 课件(共21张PPT)
文档属性
| 名称 | 17.2.2 函数的图象(1) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
17.2.2 函数的图象(1)
华师大版 八年级 下册
教学目标
教学目标:1.理解函数的图象的概念.
2.掌握画函数图象的一般步骤,能画出一些简单的函数图象.
教学重点:用描点法画函数图象.
教学难点:灵活选择自变量的值,便于描点使画图简便.注意自变量的取
值范围.
新知导入
情境引入
1、函数关系的三种表示方法:
解析法、列表法、图象法
复习与回忆
2.平面直角坐标系内的点与 成一一对应关系,它的含义是什么?
有序实数对
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
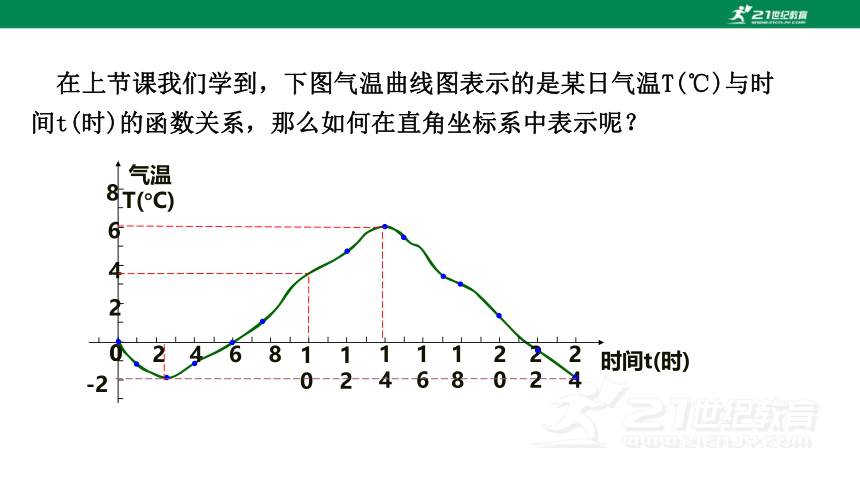
在上节课我们学到,下图气温曲线图表示的是某日气温T(℃)与时间t(时)的函数关系,那么如何在直角坐标系中表示呢?
新知讲解
合作学习
从图中我们可以看出,随着时间 t(时)的变化,相应的气温 T(℃)也随之变化.
例如,上午 10 时的气温是 2 ℃,表现在气温曲线上,就是可以找到这样的对应点,它的坐标是(10, 2).
实质上也就是说,当 t =10 时,对应的函数值 T=2. 气温曲线上每一个点的坐标 (t,T),表示时刻为 t (时)的气温是 T(℃).
气温曲线是用图象表示函数的一个实际例子.那么,什么是函数的图象呢?
提炼概念
函数的图象是由平面直角坐标系中一系列的点组成的,图象上每一点的坐标(x,y)代表了函数的一对对应值,即把自变量x与函数y的每一对对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出相应的点,这些点组成的图形,就是这个函数的图象.
典例精讲
例1 画出函数 的图象.
分析:函数图象上的点一般来说有无数多个,要把每个点都作出来得到函数图象很困难,甚至是不可能的.所以我们常作出函数图象上的一部分点,然后用光滑的曲线把这些点连接起来得到函数的图象.
请同学们想一想,怎么才能得到图象上的一部分点呢
为此,我们首先要取一些自变量x的值,求出对应的函数值y,那么以(x,y)为坐标的点就是函数图象上的点.为了表达方便,我们可以列表来表示x和y的对应关系.
解:取自变量的一些值,例如-3、-2、-1、0、1、2、3,计算出对应的函数值,列表表示:
4.5
2
0.5
0
0.5
2
4.5
x … -3 -2 -1 0 1 2 3 …
y …
…
x
o
-4
-3
-2
-1
1
2
3
4
5
-5
y
1
2
3
4
5
大家自己总结一下,看看我们在做这个函数图象的时候都经过了哪些步骤
画图象的步骤可以概括为三步:列表、描点、连线,这种画函数图象的方法叫做描点法..
(-3,4.5)
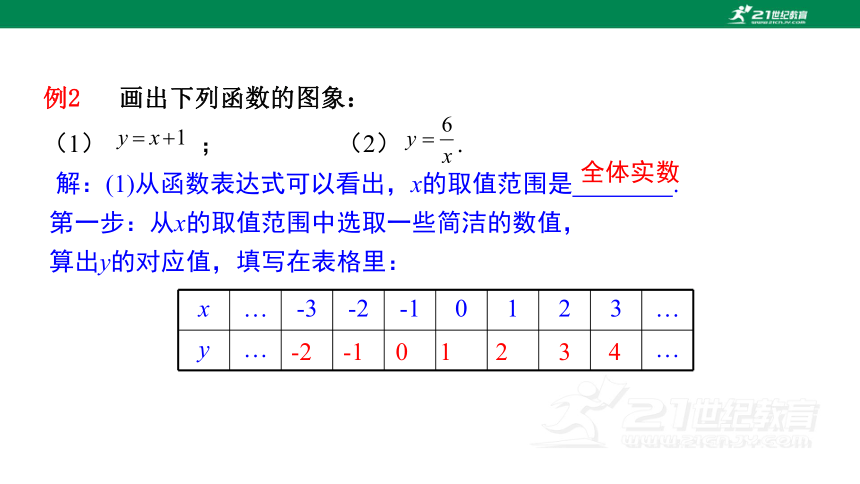
例2 画出下列函数的图象:
(1) ; (2) .
解:(1)从函数表达式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值,
算出y的对应值,填写在表格里:
x … -3 -2 -1 0 1 2 3 …
y … …
-2 -1 0 1 2 3 4
全体实数
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
当自变量的值越来越大时,对应的函数值 .
画出的图象是一条 ,
直线
越来越大
-6
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
为什么没有“0”?
(2)列表 :取一些自变量的值,并求出对应的函数值,填入表中.
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
描点: 分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.
连线: 用光滑的曲线把这些点依次连接起来.
(1,-6)
归纳概念
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应
的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,把所描出的各点用
连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
课堂练习
1.在所给的直角坐标系中画出函数y=
X的图象.
-1.5
-1
-0.5
0
0.5
1
1.5
(先填写下表,再描点、连线)
●
●
●
●
●
●
●
y
5
x
o
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
解:(1)列表
(2)描点 分别以表中
对应的x、y为横纵
坐标,在坐标系中描
出对应的点.
(3)连线 用光滑的曲
线把这些点依次连
接起来.
-6
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
(1,-6)
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
3.在同一坐标系下画出下列函数的图象,并观察、判断两图象是什么形状的图形,它们的位置关系如何。(1)y=4x-1;(2)y=4x+1.
两者均是直线,互相平行
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 …
y=4x-1 … -9 -7 -5 -3 -1 1 3 5 …
y=4x+1 … -7 -5 -3 -1 1 3 5 7 …
A(0,12)
4、如图等腰三角形的周长为12底为y,是腰为x的函数(1)写出函数关系式(2)求自变量取值范围(3)画出函数图像.
x
y
x
(1)y=12-2x
(2) 0(3)如图
y
5
x
1
2
3
4
6
o
-1
1
2
3
4
5
6
B(6,0)
11
7
8
9
10
12
解:
课堂总结
1. 什么是函数的图象
函数的图象是由直角坐标系中的一系列点组成.
图象上每一点坐标(x,y)代表了函数的一对对应值,它的
横坐标X表示自变量的某一个值,纵坐标y表示与它对应的函数值.
第一步
列表
第二步
描点
第三步
连线
2. 画函数图象的步骤是什么?
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.2.2 函数的图象(1)
华师大版 八年级 下册
教学目标
教学目标:1.理解函数的图象的概念.
2.掌握画函数图象的一般步骤,能画出一些简单的函数图象.
教学重点:用描点法画函数图象.
教学难点:灵活选择自变量的值,便于描点使画图简便.注意自变量的取
值范围.
新知导入
情境引入
1、函数关系的三种表示方法:
解析法、列表法、图象法
复习与回忆
2.平面直角坐标系内的点与 成一一对应关系,它的含义是什么?
有序实数对
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
在上节课我们学到,下图气温曲线图表示的是某日气温T(℃)与时间t(时)的函数关系,那么如何在直角坐标系中表示呢?
新知讲解
合作学习
从图中我们可以看出,随着时间 t(时)的变化,相应的气温 T(℃)也随之变化.
例如,上午 10 时的气温是 2 ℃,表现在气温曲线上,就是可以找到这样的对应点,它的坐标是(10, 2).
实质上也就是说,当 t =10 时,对应的函数值 T=2. 气温曲线上每一个点的坐标 (t,T),表示时刻为 t (时)的气温是 T(℃).
气温曲线是用图象表示函数的一个实际例子.那么,什么是函数的图象呢?
提炼概念
函数的图象是由平面直角坐标系中一系列的点组成的,图象上每一点的坐标(x,y)代表了函数的一对对应值,即把自变量x与函数y的每一对对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出相应的点,这些点组成的图形,就是这个函数的图象.
典例精讲
例1 画出函数 的图象.
分析:函数图象上的点一般来说有无数多个,要把每个点都作出来得到函数图象很困难,甚至是不可能的.所以我们常作出函数图象上的一部分点,然后用光滑的曲线把这些点连接起来得到函数的图象.
请同学们想一想,怎么才能得到图象上的一部分点呢
为此,我们首先要取一些自变量x的值,求出对应的函数值y,那么以(x,y)为坐标的点就是函数图象上的点.为了表达方便,我们可以列表来表示x和y的对应关系.
解:取自变量的一些值,例如-3、-2、-1、0、1、2、3,计算出对应的函数值,列表表示:
4.5
2
0.5
0
0.5
2
4.5
x … -3 -2 -1 0 1 2 3 …
y …
…
x
o
-4
-3
-2
-1
1
2
3
4
5
-5
y
1
2
3
4
5
大家自己总结一下,看看我们在做这个函数图象的时候都经过了哪些步骤
画图象的步骤可以概括为三步:列表、描点、连线,这种画函数图象的方法叫做描点法..
(-3,4.5)
例2 画出下列函数的图象:
(1) ; (2) .
解:(1)从函数表达式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值,
算出y的对应值,填写在表格里:
x … -3 -2 -1 0 1 2 3 …
y … …
-2 -1 0 1 2 3 4
全体实数
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
当自变量的值越来越大时,对应的函数值 .
画出的图象是一条 ,
直线
越来越大
-6
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
为什么没有“0”?
(2)列表 :取一些自变量的值,并求出对应的函数值,填入表中.
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
描点: 分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.
连线: 用光滑的曲线把这些点依次连接起来.
(1,-6)
归纳概念
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应
的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,把所描出的各点用
连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
课堂练习
1.在所给的直角坐标系中画出函数y=
X的图象.
-1.5
-1
-0.5
0
0.5
1
1.5
(先填写下表,再描点、连线)
●
●
●
●
●
●
●
y
5
x
o
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
解:(1)列表
(2)描点 分别以表中
对应的x、y为横纵
坐标,在坐标系中描
出对应的点.
(3)连线 用光滑的曲
线把这些点依次连
接起来.
-6
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
(1,-6)
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
3.在同一坐标系下画出下列函数的图象,并观察、判断两图象是什么形状的图形,它们的位置关系如何。(1)y=4x-1;(2)y=4x+1.
两者均是直线,互相平行
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 …
y=4x-1 … -9 -7 -5 -3 -1 1 3 5 …
y=4x+1 … -7 -5 -3 -1 1 3 5 7 …
A(0,12)
4、如图等腰三角形的周长为12底为y,是腰为x的函数(1)写出函数关系式(2)求自变量取值范围(3)画出函数图像.
x
y
x
(1)y=12-2x
(2) 0
y
5
x
1
2
3
4
6
o
-1
1
2
3
4
5
6
B(6,0)
11
7
8
9
10
12
解:
课堂总结
1. 什么是函数的图象
函数的图象是由直角坐标系中的一系列点组成.
图象上每一点坐标(x,y)代表了函数的一对对应值,它的
横坐标X表示自变量的某一个值,纵坐标y表示与它对应的函数值.
第一步
列表
第二步
描点
第三步
连线
2. 画函数图象的步骤是什么?
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
