2023年九年级数学中考一轮复习--与圆有关的计算(知识梳理 专题训练)(含答案)
文档属性
| 名称 | 2023年九年级数学中考一轮复习--与圆有关的计算(知识梳理 专题训练)(含答案) | 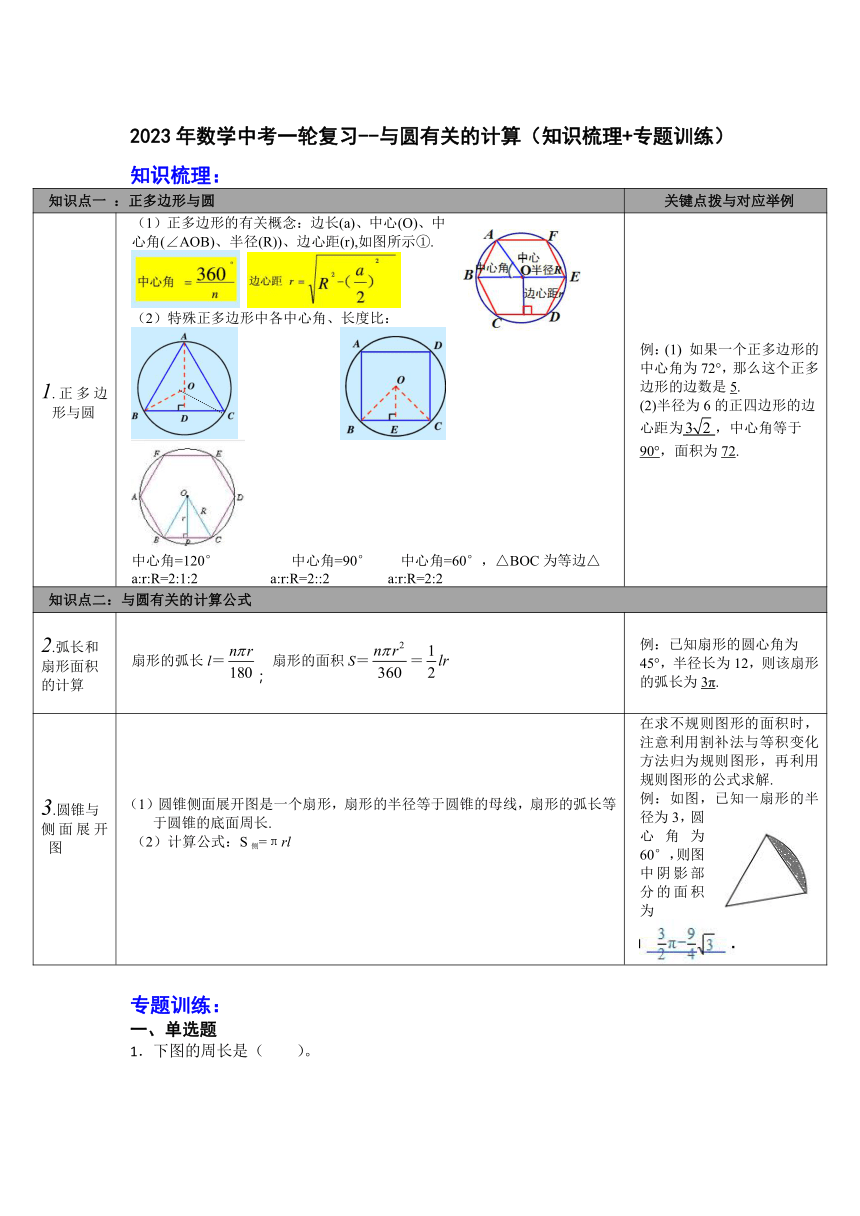 | |
| 格式 | docx | ||
| 文件大小 | 309.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 20:05:28 | ||
图片预览


文档简介
2023年数学中考一轮复习--与圆有关的计算(知识梳理+专题训练)
知识梳理:
知识点一 :正多边形与圆 关键点拨与对应举例
1.正多边形与圆 (1)正多边形的有关概念:边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①. (2)特殊正多边形中各中心角、长度比: 中心角=120° 中心角=90° 中心角=60°,△BOC为等边△ a:r:R=2:1:2 a:r:R=2::2 a:r:R=2:2 例:(1) 如果一个正多边形的中心角为72°,那么这个正多边形的边数是5. (2)半径为6的正四边形的边心距为,中心角等于90°,面积为72.
知识点二:与圆有关的计算公式
2.弧长和 扇形面积 的计算 扇形的弧长l=;扇形的面积S== 例:已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为3π.
3.圆锥与 侧面展开图 (1)圆锥侧面展开图是一个扇形,扇形的半径等于圆锥的母线,扇形的弧长等于圆锥的底面周长. (2)计算公式:S侧=πrl 在求不规则图形的面积时,注意利用割补法与等积变化方法归为规则图形,再利用规则图形的公式求解. 例:如图,已知一扇形的半径为3,圆心角为60°,则图中阴影部分的面积为
专题训练:
一、单选题
1.下图的周长是( )。
A.2π B.4π C.4π+4 D.4π+8
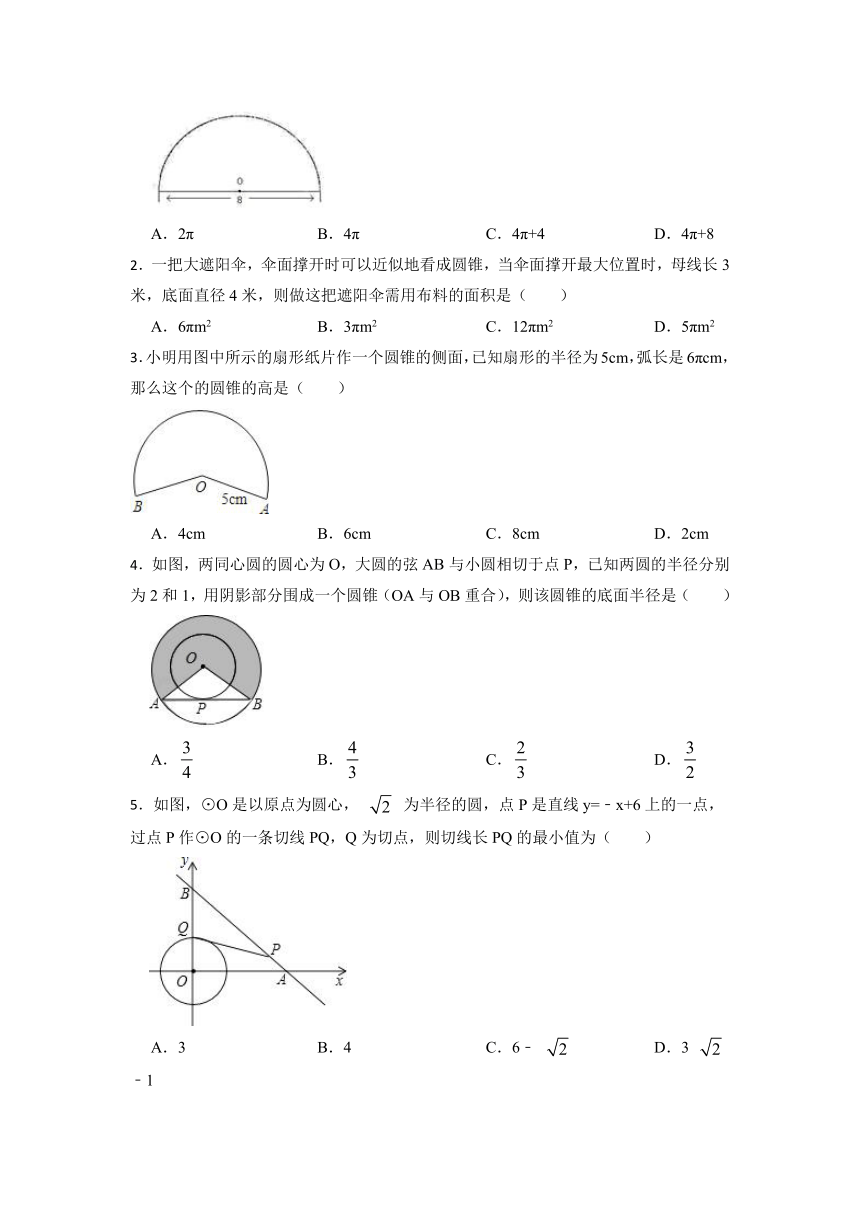
2.一把大遮阳伞,伞面撑开时可以近似地看成圆锥,当伞面撑开最大位置时,母线长3米,底面直径4米,则做这把遮阳伞需用布料的面积是( )
A.6πm2 B.3πm2 C.12πm2 D.5πm2
3.小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )
A.4cm B.6cm C.8cm D.2cm
4.如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( )
A. B. C. D.
5.如图,⊙O是以原点为圆心, 为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.3 B.4 C.6﹣ D.3 ﹣1
6.已知圆锥的母线长为12,底面圆半径为6,则圆锥的侧面积是( )
A.24π B.36π C.70π D.72π
7.如果一个圆锥的主视图是正三角形,则其侧面展开图的圆心角为
A.120 B.约156 C.180 D.约208
8.下列说法中,符合题意的个数是( )
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
A.2个 B.3个 C.4个 D.5个
9.如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
A.288° B.144° C.216° D.120°
10.如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是( ).
A.1 B. C. D.2
二、填空题
11.已知圆锥的底面半径是2cm,母线长是3cm,则圆锥侧面积是 .
12.已知圆锥的底面半径为6,母线长为8,圆锥的侧面积为 .
13.如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是 cm.
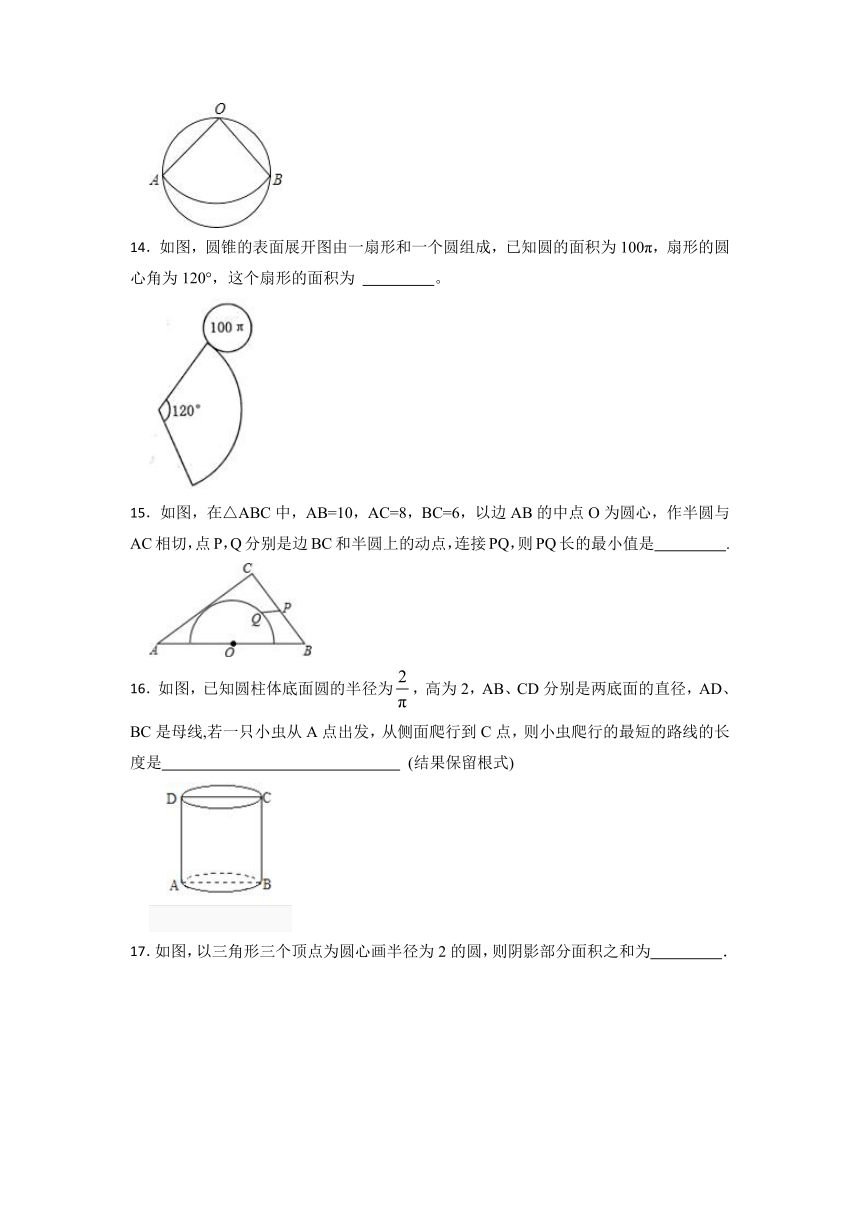
14.如图,圆锥的表面展开图由一扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,这个扇形的面积为 。
15.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是 .
16.如图,已知圆柱体底面圆的半径为,高为2,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短的路线的长度是 (结果保留根式)
17.如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为 .
18.若一圆柱的底面直径为10cm,高为15cm,则该圆柱的侧面展开图形的面积 .
三、解答题
19.上海体育馆圆形比赛场地的半径是55米,它的周长和面积各是多少?
20.下图是一盒果汁饮料.如果将这盒饮料全部倒在底面直径6cm高10cm的圆柱形杯子里,一共需要几个杯子。
21.压路机的滚筒是个圆柱,它的长是2米,滚筒横截面半径是1米,如果滚筒每分钟滚动5周,那么10分钟可压路多少平方米。前进了多少米。
22.如图①是山东舰徽的构图,采用航母 度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为 的圆锥侧面展开图(如图②),则该圆锥的母线长 为多少
23.如图,已知圆锥的底面积为 ,高 ,求该圆锥的侧面展开图的面积(结果保留 ).
24.如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 .
(1)求 点的坐标;
(2)设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】A
10.【答案】B
11.【答案】
12.【答案】48π
13.【答案】
14.【答案】300π
15.【答案】1
16.【答案】
17.【答案】
18.【答案】471cm2
19.【答案】解:3.14×(55×2)
=3.14×110
=345.4(米)
3.14×552
=3.14×3025
=9498.5(平方米)
答:它的周长是345.4米,面积是9498.5平方米。
20.【答案】解:30×12×10÷[3.14×(6÷2)2×10]
=3600÷(3.14×9×10)
=3600÷282.6
≈13(个)
答:一共需要13个杯子.
21.【答案】解:3.14×1×2×2×5×10=3.14×2×2×5×10=6.28×2×5×10=12.56×5×10=62.8×10=628(平方米)
3.14×1×2×5×10=3.14×2×5×10=6.28×5×10=31.4×10=314(米)
答:压路面积628平方米,前进314米。
22.【答案】解: 圆锥底面周长 侧面展开后扇形的弧长
在 中, ,
所以该圆锥的母线长 为 .
23.【答案】解:由题意可知: ,
圆锥的底面半径 ,
圆锥的侧面展开图的弧长等圆锥底面圆的周长
圆锥的侧面展开图的弧长
圆锥的侧面展开图的面积为
24.【答案】(1)∵BC是圆的切线,
∴BC⊥AB,
∵直线AB的解析式为,
∴直线BC的解析式为y=2x+4,令y=0,
∴2x+4=0,∴x=-2,
∴C(-2,0);
(2)PM+PN的值是定值,定值为20。将x=0代入直线,得到y=4,
∴B(4,0),再将y=0代入直线,得到x=8,
∴A(8,0),由(1)可知:C(-2,0),∵CDBC,
∴D(-4,-4),∵A(8,0),
∴直线AD的解析式为,
∵点P再线段BC上,设P(m,2m+4)(-2∵PM//x轴,
∴M(-4m,2m+4),N(6m+20,2m+4),
∴PM+PN=-4m-m+(6m+20-m)=20,即:PM+PN的值是定值,定值为20.
知识梳理:
知识点一 :正多边形与圆 关键点拨与对应举例
1.正多边形与圆 (1)正多边形的有关概念:边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①. (2)特殊正多边形中各中心角、长度比: 中心角=120° 中心角=90° 中心角=60°,△BOC为等边△ a:r:R=2:1:2 a:r:R=2::2 a:r:R=2:2 例:(1) 如果一个正多边形的中心角为72°,那么这个正多边形的边数是5. (2)半径为6的正四边形的边心距为,中心角等于90°,面积为72.
知识点二:与圆有关的计算公式
2.弧长和 扇形面积 的计算 扇形的弧长l=;扇形的面积S== 例:已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为3π.
3.圆锥与 侧面展开图 (1)圆锥侧面展开图是一个扇形,扇形的半径等于圆锥的母线,扇形的弧长等于圆锥的底面周长. (2)计算公式:S侧=πrl 在求不规则图形的面积时,注意利用割补法与等积变化方法归为规则图形,再利用规则图形的公式求解. 例:如图,已知一扇形的半径为3,圆心角为60°,则图中阴影部分的面积为
专题训练:
一、单选题
1.下图的周长是( )。
A.2π B.4π C.4π+4 D.4π+8
2.一把大遮阳伞,伞面撑开时可以近似地看成圆锥,当伞面撑开最大位置时,母线长3米,底面直径4米,则做这把遮阳伞需用布料的面积是( )
A.6πm2 B.3πm2 C.12πm2 D.5πm2
3.小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )
A.4cm B.6cm C.8cm D.2cm
4.如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( )
A. B. C. D.
5.如图,⊙O是以原点为圆心, 为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.3 B.4 C.6﹣ D.3 ﹣1
6.已知圆锥的母线长为12,底面圆半径为6,则圆锥的侧面积是( )
A.24π B.36π C.70π D.72π
7.如果一个圆锥的主视图是正三角形,则其侧面展开图的圆心角为
A.120 B.约156 C.180 D.约208
8.下列说法中,符合题意的个数是( )
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
A.2个 B.3个 C.4个 D.5个
9.如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
A.288° B.144° C.216° D.120°
10.如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是( ).
A.1 B. C. D.2
二、填空题
11.已知圆锥的底面半径是2cm,母线长是3cm,则圆锥侧面积是 .
12.已知圆锥的底面半径为6,母线长为8,圆锥的侧面积为 .
13.如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是 cm.
14.如图,圆锥的表面展开图由一扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,这个扇形的面积为 。
15.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是 .
16.如图,已知圆柱体底面圆的半径为,高为2,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短的路线的长度是 (结果保留根式)
17.如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为 .
18.若一圆柱的底面直径为10cm,高为15cm,则该圆柱的侧面展开图形的面积 .
三、解答题
19.上海体育馆圆形比赛场地的半径是55米,它的周长和面积各是多少?
20.下图是一盒果汁饮料.如果将这盒饮料全部倒在底面直径6cm高10cm的圆柱形杯子里,一共需要几个杯子。
21.压路机的滚筒是个圆柱,它的长是2米,滚筒横截面半径是1米,如果滚筒每分钟滚动5周,那么10分钟可压路多少平方米。前进了多少米。
22.如图①是山东舰徽的构图,采用航母 度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为 的圆锥侧面展开图(如图②),则该圆锥的母线长 为多少
23.如图,已知圆锥的底面积为 ,高 ,求该圆锥的侧面展开图的面积(结果保留 ).
24.如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 .
(1)求 点的坐标;
(2)设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】A
10.【答案】B
11.【答案】
12.【答案】48π
13.【答案】
14.【答案】300π
15.【答案】1
16.【答案】
17.【答案】
18.【答案】471cm2
19.【答案】解:3.14×(55×2)
=3.14×110
=345.4(米)
3.14×552
=3.14×3025
=9498.5(平方米)
答:它的周长是345.4米,面积是9498.5平方米。
20.【答案】解:30×12×10÷[3.14×(6÷2)2×10]
=3600÷(3.14×9×10)
=3600÷282.6
≈13(个)
答:一共需要13个杯子.
21.【答案】解:3.14×1×2×2×5×10=3.14×2×2×5×10=6.28×2×5×10=12.56×5×10=62.8×10=628(平方米)
3.14×1×2×5×10=3.14×2×5×10=6.28×5×10=31.4×10=314(米)
答:压路面积628平方米,前进314米。
22.【答案】解: 圆锥底面周长 侧面展开后扇形的弧长
在 中, ,
所以该圆锥的母线长 为 .
23.【答案】解:由题意可知: ,
圆锥的底面半径 ,
圆锥的侧面展开图的弧长等圆锥底面圆的周长
圆锥的侧面展开图的弧长
圆锥的侧面展开图的面积为
24.【答案】(1)∵BC是圆的切线,
∴BC⊥AB,
∵直线AB的解析式为,
∴直线BC的解析式为y=2x+4,令y=0,
∴2x+4=0,∴x=-2,
∴C(-2,0);
(2)PM+PN的值是定值,定值为20。将x=0代入直线,得到y=4,
∴B(4,0),再将y=0代入直线,得到x=8,
∴A(8,0),由(1)可知:C(-2,0),∵CDBC,
∴D(-4,-4),∵A(8,0),
∴直线AD的解析式为,
∵点P再线段BC上,设P(m,2m+4)(-2
∴M(-4m,2m+4),N(6m+20,2m+4),
∴PM+PN=-4m-m+(6m+20-m)=20,即:PM+PN的值是定值,定值为20.
同课章节目录
