北师大版七下数学 第五章 生活中的轴对称 复习学案 (无答案)
文档属性
| 名称 | 北师大版七下数学 第五章 生活中的轴对称 复习学案 (无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览

文档简介
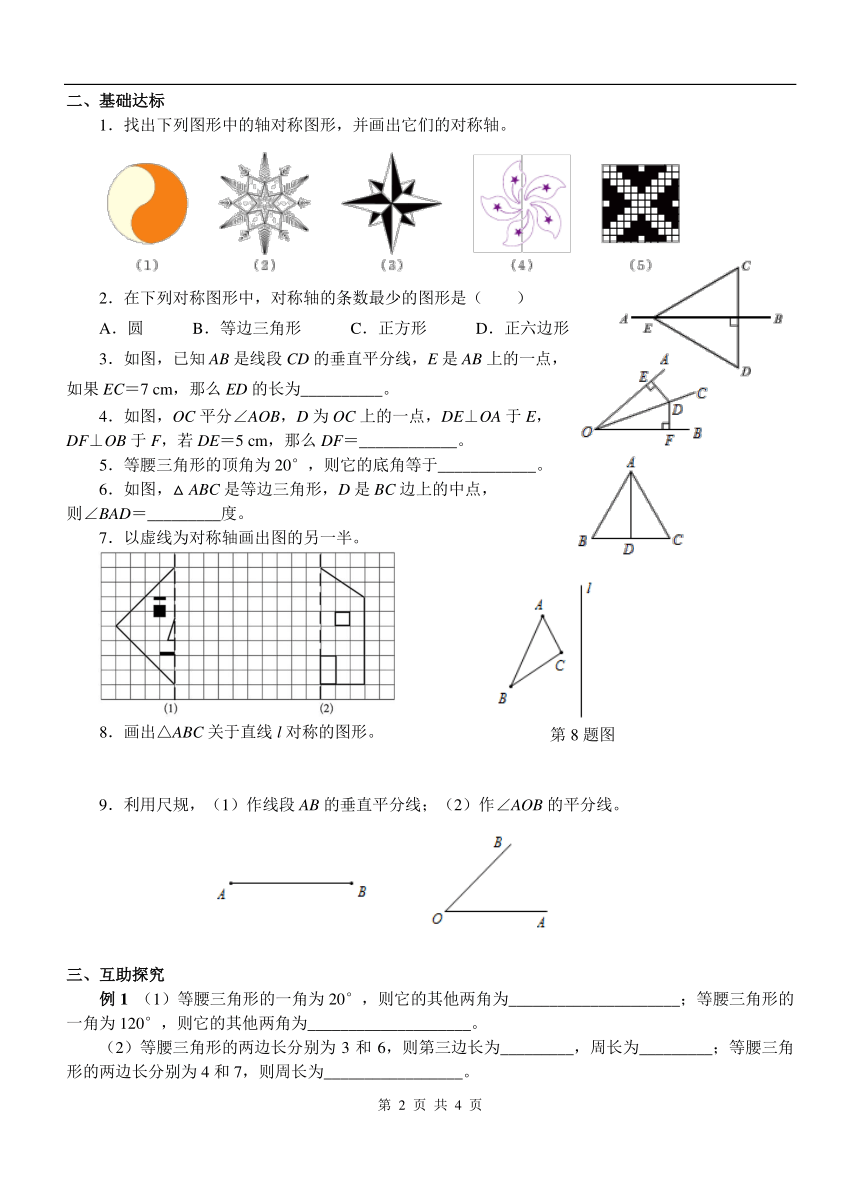
第五章生活中的轴对称复习
第 周星期 班别 姓名 学号________
【学习目标】
1.进一步认识轴对称及其基本性质.
2.进一步掌握等腰三角形、线段、角的性质,并能运用上述性质解题.
3.按要求能够作出简单平面图形经过轴对称后的图形.
4.能利用尺规作已知线段的垂直平分线,已知角的平分线.
【学习重点】复习轴对称的基本性质,简单的轴对称图形,并会运用轴对称的性质解决相关问题.
【学习难点】灵活运用轴对称的性质解决相关问题.
【学习过程】
一、知识梳理,归纳升华
1.请画出本章的知识结构图
2.重点知识
(1)轴对称的性质:__________________________________________________________________
_________________________________________________。
(2)等腰三角形的性质:______________________________________________________________
_________________________________________________________________________________________
____________________________________________________________________________________。
(3)等边三角形的性质:_____________________________________________________________。
(4)线段垂直平分线的性质:_________________________________________________________。
(5)角平分线的性质:__________________________________________________________。
二、基础达标
1.找出下列图形中的轴对称图形,并画出它们的对称轴。
2.在下列对称图形中,对称轴的条数最少的图形是( )
A.圆 B.等边三角形 C.正方形 D.正六边形
3.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,
如果EC=7 cm,那么ED的长为__________。
4.如图,OC平分∠AOB,D为OC上的一点,DE⊥OA于E,
DF⊥OB于F,若DE=5 cm,那么DF=____________。
5.等腰三角形的顶角为20°,则它的底角等于____________。
6.如图,△ABC是等边三角形,D是BC边上的中点,
则∠BAD=_________度。
7.以虚线为对称轴画出图的另一半。
8.画出△ABC关于直线l对称的图形。
9.利用尺规,(1)作线段AB的垂直平分线;(2)作∠AOB的平分线。
三、互助探究
例1 (1)等腰三角形的一角为20°,则它的其他两角为_____________________;等腰三角形的一角为120°,则它的其他两角为____________________。
(2)等腰三角形的两边长分别为3和6,则第三边长为_________,周长为_________;等腰三角形的两边长分别为4和7,则周长为_________________。
例2 如图,在△ABC中,∠C=90°,∠A=36°,DE是线段AB的垂直平分线,交AB于点D,交AC于点E。求∠EBC的度数。
例3 如图,已知直线l及其同侧两点A,B。
(1)在直线l上求一点P,使PA+PB最短;(2)在直线l上求一点O,OA=OB(尺规作图)。
四、分层提高
1.如图,在Rt△ABC中,BE平分∠ABC,ED⊥AB
于D,AC=3 cm,则AE+DE=______cm。
2.如图,在△ABC中,AB边上的垂直平分线DE交
AB于D,交AC于E,AC=9 cm,△BCE的周长为15 cm,
则BC的长为____________。
3.如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,求∠ADE的度数。
五、总结归纳
谈谈这节课的收获
我容易出错的地方是
六、巩固反馈
(一)基础训练
1.下列几何图形中,其中一定是轴对称图形的有( )
①线段;②角;③等腰三角形;④平行四边形;⑤正方形;⑥直角三角形
A.3个 B.4个 C.5个 D.6个
2.如图,△ABC与△DEF关于直线MN成轴对称,
则以下结论错误的是( )
A.AB∥DF B.∠B=∠E
C.AB=DE D.点A,D所连的线段被MN垂直平分
3.等腰三角形的顶角为100°,则它的底角的度数为___________。
4.等腰三角形的周长为22 cm,其中一边的长为8 cm,则其余两边长分别为________________。
5.OC平分∠AOB,D为OC上一点,DE⊥OB于E,
若DE=4 cm,则D到OA的距离为_______。
6.如图,在△ABC中,已知DE是AC的垂直平分线,
AB=8,BC=10,则△ABD的周长等于________。
7.试找出如图所示的每个正多边形对称轴的条数,并填入表格中。
正多边形的边数 3 4 5 6 7 8
对称轴的条数
根据上表,可猜想一个正n边形对称轴的条数为________条。
8.如图,是由以AB为底边的等腰三角形ABC和以AB为直径的半圆组成,借助尺规作出它的对称轴。
(二)能力提升
9.如图,在△ABC中,AB=AC,M是BC的中点,过点M作ME⊥AB,MF⊥AC,垂足分别为E,F。求证:ME=MF。
生活中的轴对称
轴对称
简单的轴对称图形
利用轴对称进行设计
轴对称的性质
第8题图
第 4 页 共 4 页
第 周星期 班别 姓名 学号________
【学习目标】
1.进一步认识轴对称及其基本性质.
2.进一步掌握等腰三角形、线段、角的性质,并能运用上述性质解题.
3.按要求能够作出简单平面图形经过轴对称后的图形.
4.能利用尺规作已知线段的垂直平分线,已知角的平分线.
【学习重点】复习轴对称的基本性质,简单的轴对称图形,并会运用轴对称的性质解决相关问题.
【学习难点】灵活运用轴对称的性质解决相关问题.
【学习过程】
一、知识梳理,归纳升华
1.请画出本章的知识结构图
2.重点知识
(1)轴对称的性质:__________________________________________________________________
_________________________________________________。
(2)等腰三角形的性质:______________________________________________________________
_________________________________________________________________________________________
____________________________________________________________________________________。
(3)等边三角形的性质:_____________________________________________________________。
(4)线段垂直平分线的性质:_________________________________________________________。
(5)角平分线的性质:__________________________________________________________。
二、基础达标
1.找出下列图形中的轴对称图形,并画出它们的对称轴。
2.在下列对称图形中,对称轴的条数最少的图形是( )
A.圆 B.等边三角形 C.正方形 D.正六边形
3.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,
如果EC=7 cm,那么ED的长为__________。
4.如图,OC平分∠AOB,D为OC上的一点,DE⊥OA于E,
DF⊥OB于F,若DE=5 cm,那么DF=____________。
5.等腰三角形的顶角为20°,则它的底角等于____________。
6.如图,△ABC是等边三角形,D是BC边上的中点,
则∠BAD=_________度。
7.以虚线为对称轴画出图的另一半。
8.画出△ABC关于直线l对称的图形。
9.利用尺规,(1)作线段AB的垂直平分线;(2)作∠AOB的平分线。
三、互助探究
例1 (1)等腰三角形的一角为20°,则它的其他两角为_____________________;等腰三角形的一角为120°,则它的其他两角为____________________。
(2)等腰三角形的两边长分别为3和6,则第三边长为_________,周长为_________;等腰三角形的两边长分别为4和7,则周长为_________________。
例2 如图,在△ABC中,∠C=90°,∠A=36°,DE是线段AB的垂直平分线,交AB于点D,交AC于点E。求∠EBC的度数。
例3 如图,已知直线l及其同侧两点A,B。
(1)在直线l上求一点P,使PA+PB最短;(2)在直线l上求一点O,OA=OB(尺规作图)。
四、分层提高
1.如图,在Rt△ABC中,BE平分∠ABC,ED⊥AB
于D,AC=3 cm,则AE+DE=______cm。
2.如图,在△ABC中,AB边上的垂直平分线DE交
AB于D,交AC于E,AC=9 cm,△BCE的周长为15 cm,
则BC的长为____________。
3.如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,求∠ADE的度数。
五、总结归纳
谈谈这节课的收获
我容易出错的地方是
六、巩固反馈
(一)基础训练
1.下列几何图形中,其中一定是轴对称图形的有( )
①线段;②角;③等腰三角形;④平行四边形;⑤正方形;⑥直角三角形
A.3个 B.4个 C.5个 D.6个
2.如图,△ABC与△DEF关于直线MN成轴对称,
则以下结论错误的是( )
A.AB∥DF B.∠B=∠E
C.AB=DE D.点A,D所连的线段被MN垂直平分
3.等腰三角形的顶角为100°,则它的底角的度数为___________。
4.等腰三角形的周长为22 cm,其中一边的长为8 cm,则其余两边长分别为________________。
5.OC平分∠AOB,D为OC上一点,DE⊥OB于E,
若DE=4 cm,则D到OA的距离为_______。
6.如图,在△ABC中,已知DE是AC的垂直平分线,
AB=8,BC=10,则△ABD的周长等于________。
7.试找出如图所示的每个正多边形对称轴的条数,并填入表格中。
正多边形的边数 3 4 5 6 7 8
对称轴的条数
根据上表,可猜想一个正n边形对称轴的条数为________条。
8.如图,是由以AB为底边的等腰三角形ABC和以AB为直径的半圆组成,借助尺规作出它的对称轴。
(二)能力提升
9.如图,在△ABC中,AB=AC,M是BC的中点,过点M作ME⊥AB,MF⊥AC,垂足分别为E,F。求证:ME=MF。
生活中的轴对称
轴对称
简单的轴对称图形
利用轴对称进行设计
轴对称的性质
第8题图
第 4 页 共 4 页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
