北师大版七下数学 第五单元生活中的轴对称 单元测试 (含解析)
文档属性
| 名称 | 北师大版七下数学 第五单元生活中的轴对称 单元测试 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 630.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 08:11:02 | ||
图片预览


文档简介
第五章《生活中的轴对称》
单元评价检测(五)
(45分钟 100分)
一、选择题(每小题4分,共28分)
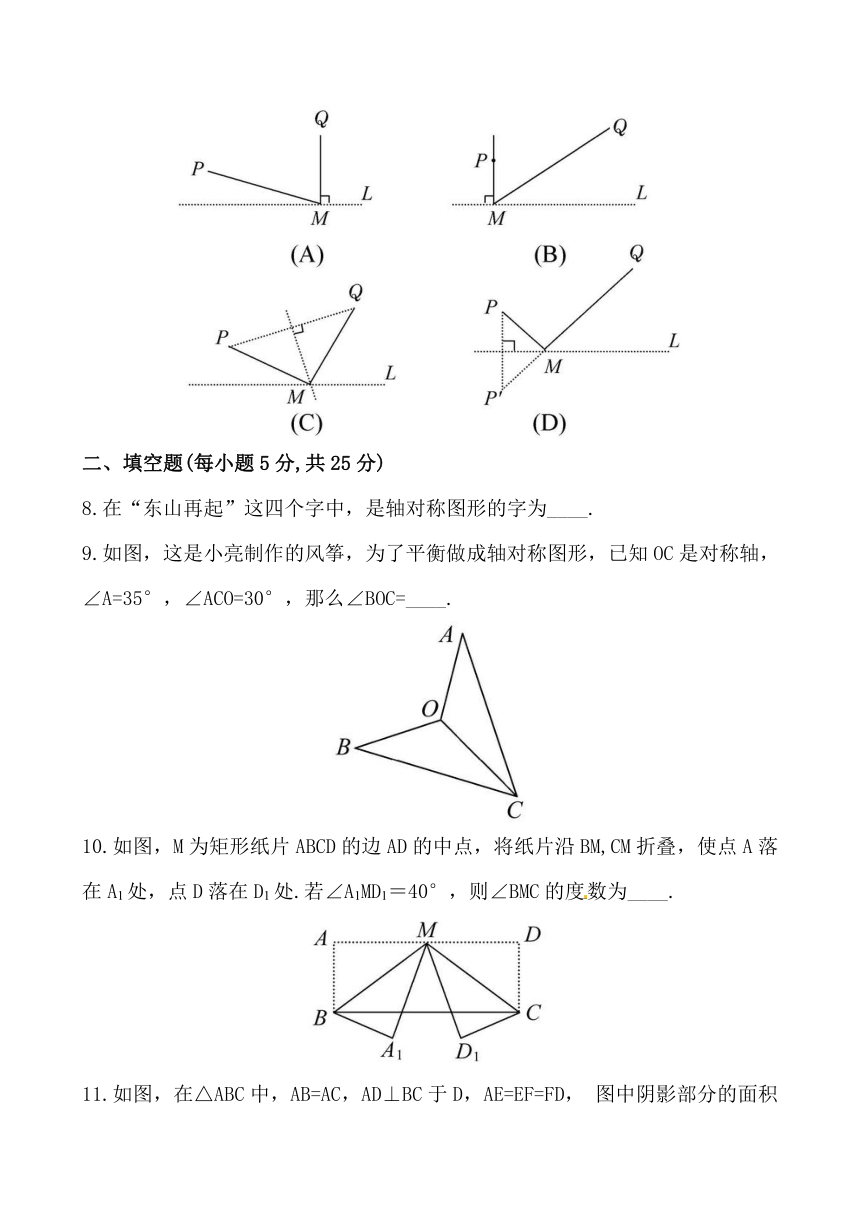
1.小华将一张如图所示矩形纸片沿对角线剪开,他利用所得的两个直角三角形通过图形变换构成了下列四个图形,这四个图形中不是轴对称图形的是( )
2.如图是一台球桌面示意图,图中小正方形的边长均相等.黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
(A)① (B)② (C)⑤ (D)⑥
3.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
(A)6 (B)7 (C)8 (D)9
4.如图,在△ABC中,AB=a,AC=b,BC边上的垂直平分线DE交BC,BA分别于点D,E,则△AEC的周长等于( )
(A)a+b (B)2a+b
(C)a+2b (D)2a+2b
5.下列大写英文字母中,是轴对称图形的有( )
(A)4个 (B)5个 (C)6个 (D)7个
6.将一张正方形的纸沿对角线对折后可以得到一个等腰直角三角形,再将等腰直角三角形对折使它的两个锐角重合,又得到一个小等腰直角三角形,在这个小等腰直角三角形上任意剪一个图案,展开后它至少有几条对称轴( )
(A)1条 (B)2条 (C)3条 (D)4条
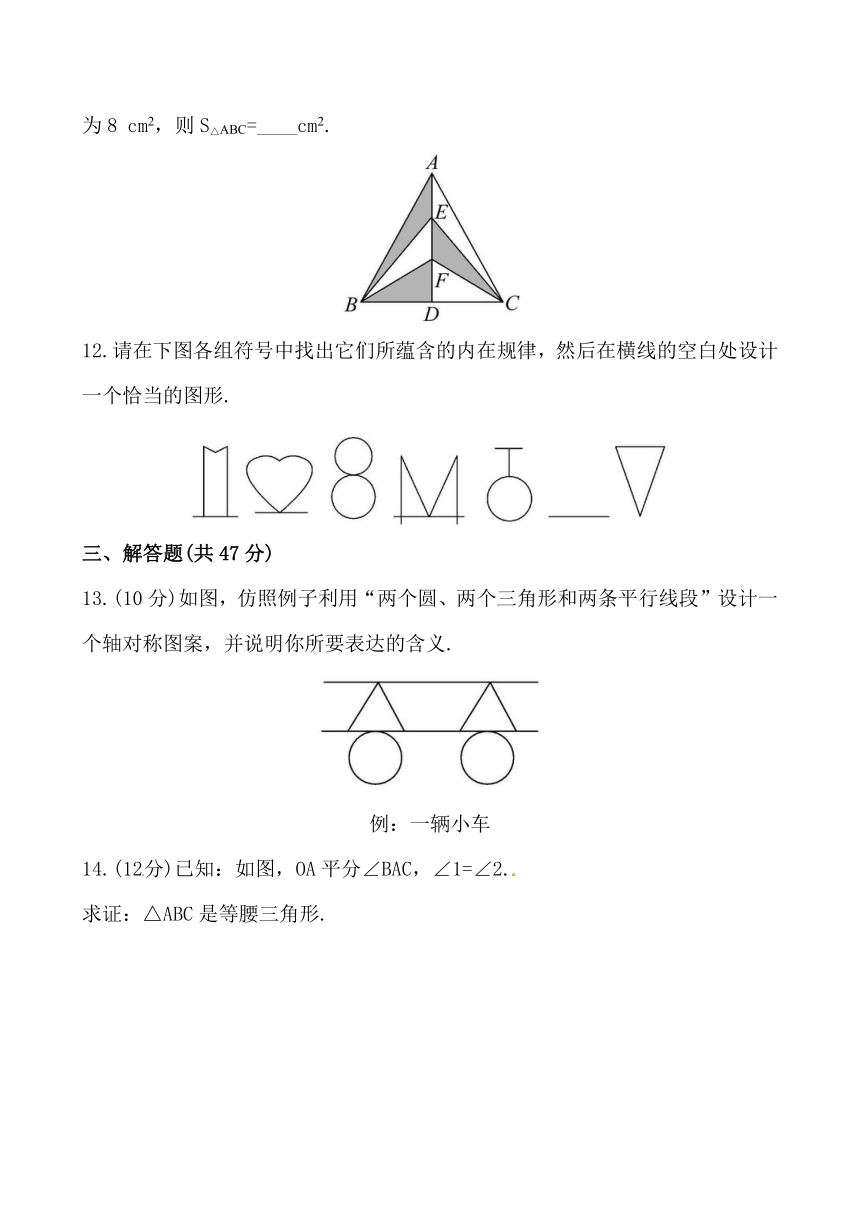
7.如图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )
二、填空题(每小题5分,共25分)
8.在“东山再起”这四个字中,是轴对称图形的字为____.
9.如图,这是小亮制作的风筝,为了平衡做成轴对称图形,已知OC是对称轴,∠A=35°,∠ACO=30°,那么∠BOC=____.
10.如图,M为矩形纸片ABCD的边AD的中点,将纸片沿BM,CM折叠,使点A落在A1处,点D落在D1处.若∠A1MD1=40°,则∠BMC的度数为____.
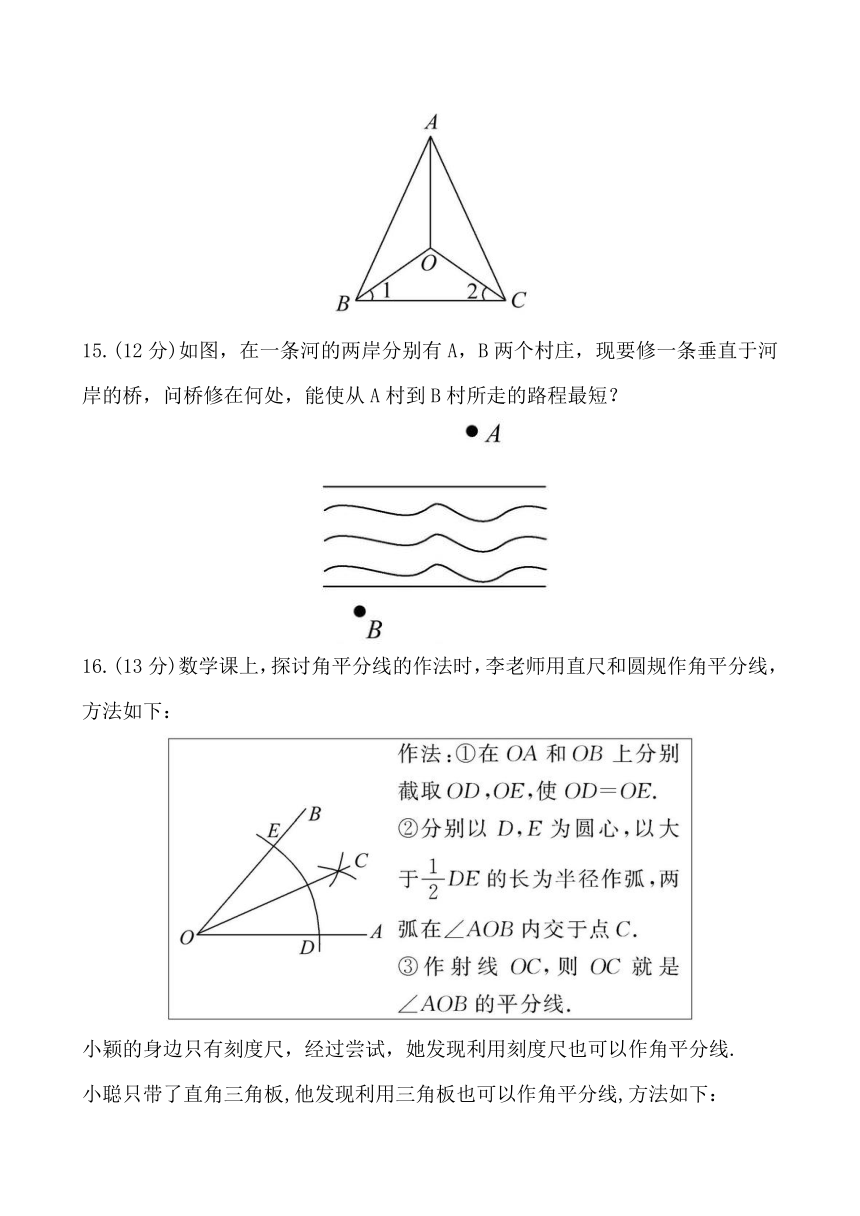
11.如图,在△ABC中,AB=AC,AD⊥BC于D,AE=EF=FD, 图中阴影部分的面积为8 cm2,则S△ABC=____cm2.
12.请在下图各组符号中找出它们所蕴含的内在规律,然后在横线的空白处设计一个恰当的图形.
三、解答题(共47分)
13.(10分)如图,仿照例子利用“两个圆、两个三角形和两条平行线段”设计一个轴对称图案,并说明你所要表达的含义.
例:一辆小车
14.(12分)已知:如图,OA平分∠BAC,∠1=∠2.
求证:△ABC是等腰三角形.
15.(12分)如图,在一条河的两岸分别有A,B两个村庄,现要修一条垂直于河岸的桥,问桥修在何处,能使从A村到B村所走的路程最短?
16.(13分)数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:
小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
小聪只带了直角三角板,他发现利用三角板也可以作角平分线,方法如下:
步骤:①利用三角板上的刻度,在OA和OB上分别截取OM,ON,使OM=ON.
②分别过M,N作OM,ON的垂线,交于点P.
③作射线OP,则OP为∠AOB的平分线.
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是______.
(2)小聪的作法正确吗?请说明理由.
(3)请你帮小颖设计用刻度尺作角平分线的方法(要求:作出图形,写出作图步骤,不予证明).
答案解析
1.【解析】选A.根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,分析各图形的特征可得.
2.【解析】选A. 根据轴对称的性质可知,台球走过的路径如图所示.
3.【解析】选D.因为∠ABC,∠ACB的平分线相交于点E,
所以∠MBE=∠EBC,∠ECN=∠ECB,
因为MN∥BC,所以∠EBC=∠MEB,∠NEC=∠ECB,
所以∠MBE=∠MEB,∠NEC=∠ECN,
所以BM=ME,EN=CN.又MN=ME+EN,
所以MN=BM+CN.因为BM+CN=9,
所以MN=9.
4.【解析】选A.因为DE垂直且平分BC,所以BE=CE.
因为AB=AE+BE=AE+CE,AB=a,AC=b,
所以△AEC的周长为:AE+CE+AC=a+b.
5.【解析】选A.由轴对称的定义可知有D,H,M,X共4个字母是轴对称图形.
6.【解析】选B.因为正方形的纸经过了两次折叠.
7.【解析】选D.作点P关于直线L的对称点P′,连接QP′交直线L于M.根据两点之间,线段最短,可知选项D所需管道最短.
8.【解析】由轴对称的定义可知“东山再起”只有“山”是轴对称图形.
答案:山
9.【解析】因为∠A=35°,∠ACO=30°,
所以∠AOC=180°-35°-30°=115°,
所以∠BOC=∠AOC=115°
答案:115°
10.【解析】因为∠A1MD1=40°,所以∠A1MA+∠DMD1=180°-40°=140°.
根据折叠的性质,得∠A1MB=∠AMB,∠D1MC=∠DMC,
所以∠BMC=140°×+40°=110°.
答案:110°
11.【解析】由等腰三角形的轴对称性得,阴影部分的面积等于△ABC面积的一半,所以△ABC的面积为16 cm2.
答案:16
12.【解析】从图中可以发现所有的图形都是轴对称图形,而且图形从左到右分别是数字1~7,所以画一个轴对称图形且数字为6即可.
答案:
13.【解析】学生只要能举出一例即可.
两盏吊着的灯
14.【证明】作OE⊥AB于E,OF⊥AC于F,
因为∠3=∠4,所以OE=OF.
因为∠1=∠2,所以OB=OC.
所以Rt△OBE≌Rt△OCF(HL),
所以∠5=∠6,
所以∠1+∠5=∠2+∠6.
即∠ABC=∠ACB.
所以△ABC是等腰三角形.
15.【解析】如图所示,过点A作MN的垂线,并在垂线上截取AA′等于河的宽度,连接A′B,交EF于点Q.过点Q作QP⊥MN,垂足为P,则QP就是所要修的桥的位置.
16.【解析】(1)SSS
(2)小聪的作法正确.
理由:因为PM⊥OM , PN⊥ON,
所以∠OMP=∠ONP=90°.
在Rt△OMP和Rt△ONP中,
因为OP=OP,OM=ON,
所以Rt△OMP≌Rt△ONP(HL).
所以∠MOP=∠NOP,所以OP平分∠AOB.
(3)如图所示.
步骤:①利用刻度尺在OA,OB上分别截取OG=OH.
②连结GH,利用刻度尺作出GH的中点Q.③作射线OQ.则OQ即为∠AOB的平分线.
单元评价检测(五)
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.小华将一张如图所示矩形纸片沿对角线剪开,他利用所得的两个直角三角形通过图形变换构成了下列四个图形,这四个图形中不是轴对称图形的是( )
2.如图是一台球桌面示意图,图中小正方形的边长均相等.黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
(A)① (B)② (C)⑤ (D)⑥
3.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
(A)6 (B)7 (C)8 (D)9
4.如图,在△ABC中,AB=a,AC=b,BC边上的垂直平分线DE交BC,BA分别于点D,E,则△AEC的周长等于( )
(A)a+b (B)2a+b
(C)a+2b (D)2a+2b
5.下列大写英文字母中,是轴对称图形的有( )
(A)4个 (B)5个 (C)6个 (D)7个
6.将一张正方形的纸沿对角线对折后可以得到一个等腰直角三角形,再将等腰直角三角形对折使它的两个锐角重合,又得到一个小等腰直角三角形,在这个小等腰直角三角形上任意剪一个图案,展开后它至少有几条对称轴( )
(A)1条 (B)2条 (C)3条 (D)4条
7.如图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )
二、填空题(每小题5分,共25分)
8.在“东山再起”这四个字中,是轴对称图形的字为____.
9.如图,这是小亮制作的风筝,为了平衡做成轴对称图形,已知OC是对称轴,∠A=35°,∠ACO=30°,那么∠BOC=____.
10.如图,M为矩形纸片ABCD的边AD的中点,将纸片沿BM,CM折叠,使点A落在A1处,点D落在D1处.若∠A1MD1=40°,则∠BMC的度数为____.
11.如图,在△ABC中,AB=AC,AD⊥BC于D,AE=EF=FD, 图中阴影部分的面积为8 cm2,则S△ABC=____cm2.
12.请在下图各组符号中找出它们所蕴含的内在规律,然后在横线的空白处设计一个恰当的图形.
三、解答题(共47分)
13.(10分)如图,仿照例子利用“两个圆、两个三角形和两条平行线段”设计一个轴对称图案,并说明你所要表达的含义.
例:一辆小车
14.(12分)已知:如图,OA平分∠BAC,∠1=∠2.
求证:△ABC是等腰三角形.
15.(12分)如图,在一条河的两岸分别有A,B两个村庄,现要修一条垂直于河岸的桥,问桥修在何处,能使从A村到B村所走的路程最短?
16.(13分)数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:
小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
小聪只带了直角三角板,他发现利用三角板也可以作角平分线,方法如下:
步骤:①利用三角板上的刻度,在OA和OB上分别截取OM,ON,使OM=ON.
②分别过M,N作OM,ON的垂线,交于点P.
③作射线OP,则OP为∠AOB的平分线.
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是______.
(2)小聪的作法正确吗?请说明理由.
(3)请你帮小颖设计用刻度尺作角平分线的方法(要求:作出图形,写出作图步骤,不予证明).
答案解析
1.【解析】选A.根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,分析各图形的特征可得.
2.【解析】选A. 根据轴对称的性质可知,台球走过的路径如图所示.
3.【解析】选D.因为∠ABC,∠ACB的平分线相交于点E,
所以∠MBE=∠EBC,∠ECN=∠ECB,
因为MN∥BC,所以∠EBC=∠MEB,∠NEC=∠ECB,
所以∠MBE=∠MEB,∠NEC=∠ECN,
所以BM=ME,EN=CN.又MN=ME+EN,
所以MN=BM+CN.因为BM+CN=9,
所以MN=9.
4.【解析】选A.因为DE垂直且平分BC,所以BE=CE.
因为AB=AE+BE=AE+CE,AB=a,AC=b,
所以△AEC的周长为:AE+CE+AC=a+b.
5.【解析】选A.由轴对称的定义可知有D,H,M,X共4个字母是轴对称图形.
6.【解析】选B.因为正方形的纸经过了两次折叠.
7.【解析】选D.作点P关于直线L的对称点P′,连接QP′交直线L于M.根据两点之间,线段最短,可知选项D所需管道最短.
8.【解析】由轴对称的定义可知“东山再起”只有“山”是轴对称图形.
答案:山
9.【解析】因为∠A=35°,∠ACO=30°,
所以∠AOC=180°-35°-30°=115°,
所以∠BOC=∠AOC=115°
答案:115°
10.【解析】因为∠A1MD1=40°,所以∠A1MA+∠DMD1=180°-40°=140°.
根据折叠的性质,得∠A1MB=∠AMB,∠D1MC=∠DMC,
所以∠BMC=140°×+40°=110°.
答案:110°
11.【解析】由等腰三角形的轴对称性得,阴影部分的面积等于△ABC面积的一半,所以△ABC的面积为16 cm2.
答案:16
12.【解析】从图中可以发现所有的图形都是轴对称图形,而且图形从左到右分别是数字1~7,所以画一个轴对称图形且数字为6即可.
答案:
13.【解析】学生只要能举出一例即可.
两盏吊着的灯
14.【证明】作OE⊥AB于E,OF⊥AC于F,
因为∠3=∠4,所以OE=OF.
因为∠1=∠2,所以OB=OC.
所以Rt△OBE≌Rt△OCF(HL),
所以∠5=∠6,
所以∠1+∠5=∠2+∠6.
即∠ABC=∠ACB.
所以△ABC是等腰三角形.
15.【解析】如图所示,过点A作MN的垂线,并在垂线上截取AA′等于河的宽度,连接A′B,交EF于点Q.过点Q作QP⊥MN,垂足为P,则QP就是所要修的桥的位置.
16.【解析】(1)SSS
(2)小聪的作法正确.
理由:因为PM⊥OM , PN⊥ON,
所以∠OMP=∠ONP=90°.
在Rt△OMP和Rt△ONP中,
因为OP=OP,OM=ON,
所以Rt△OMP≌Rt△ONP(HL).
所以∠MOP=∠NOP,所以OP平分∠AOB.
(3)如图所示.
步骤:①利用刻度尺在OA,OB上分别截取OG=OH.
②连结GH,利用刻度尺作出GH的中点Q.③作射线OQ.则OQ即为∠AOB的平分线.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
