14.2 三角形全等的判定 课件
图片预览



文档简介
课件18张PPT。14.2 三角形全等的判定
第一课时
小明家里的柜子上镶有两块形状、大小完全一样的三角形玻
璃装饰板。其中的一块被打碎了,妈妈让他再去配一块一样
的。小明要告诉师傅三角形的几个要素,才能使得新配的玻
璃和没打碎的三角形完全一样呢?
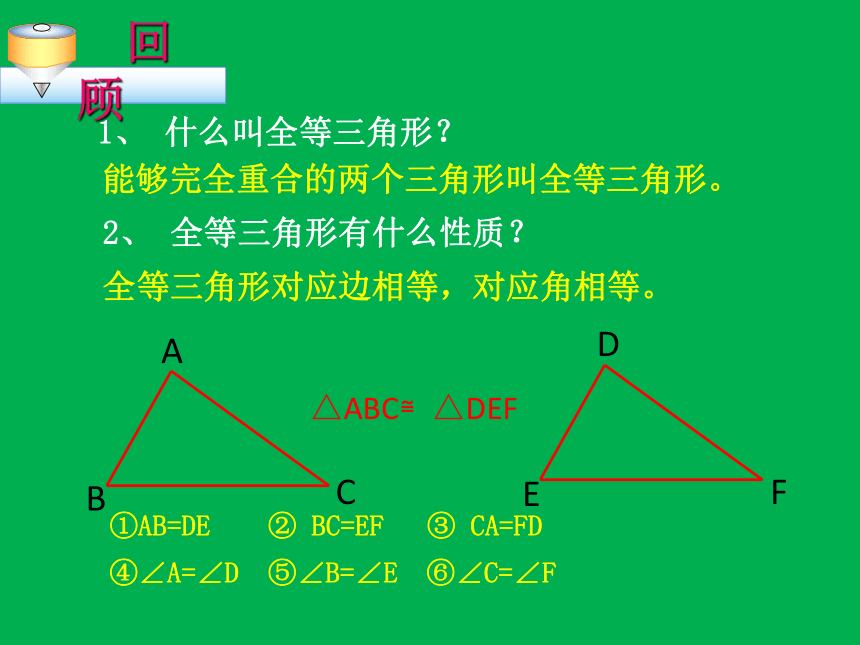
④∠A=∠D ⑤∠B=∠E ⑥∠C=∠F 1、 什么叫全等三角形?能够完全重合的两个三角形叫全等三角形。2、 全等三角形有什么性质?△ABC≌△DEF①AB=DE ② BC=EF ③ CA=FD 全等三角形对应边相等,对应角相等。元素能不能尽可能的少呢?小明要告诉师傅三角形的几个要素,才能使得新
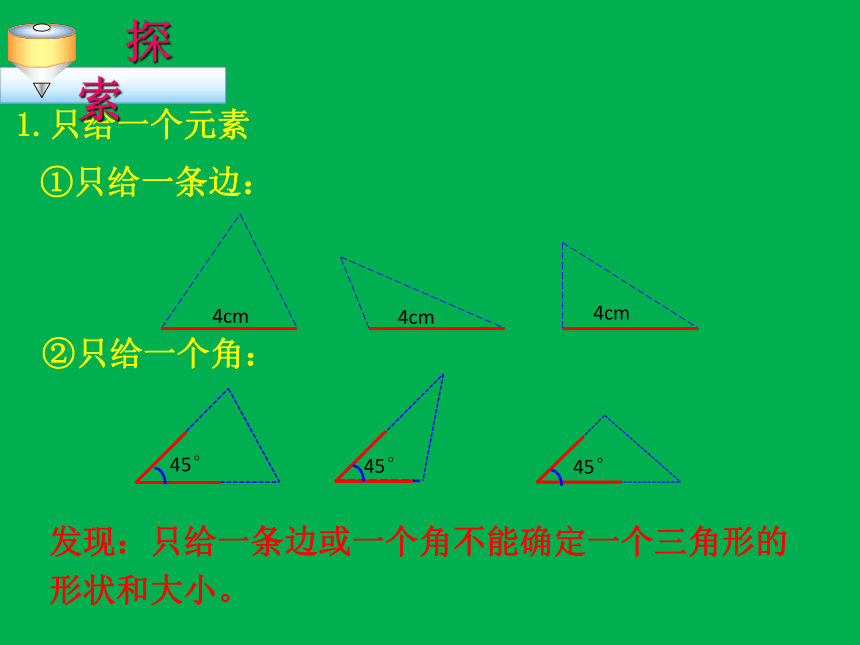
配的玻璃和没打碎的三角形完全一样呢?1.只给一个元素①只给一条边:②只给一个角:发现:只给一条边或一个角不能确定一个三角形的
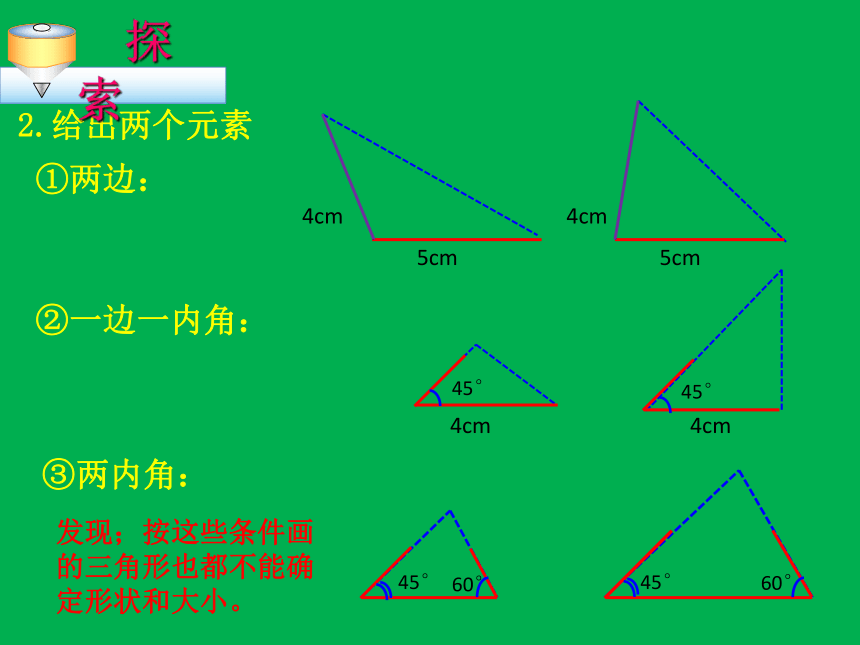
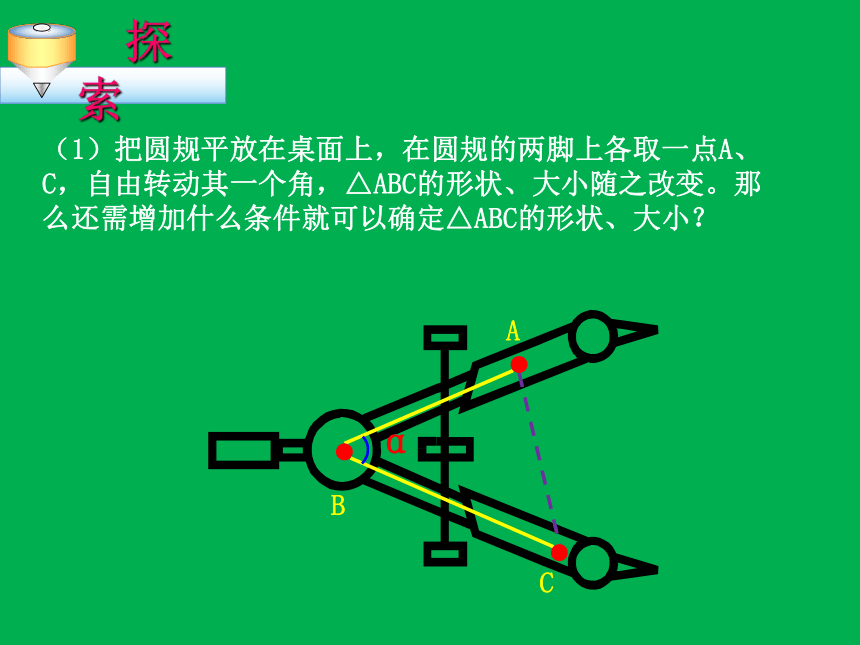
形状和大小。2.给出两个元素①两边:②一边一内角:③两内角:发现;按这些条件画的三角形也都不能确定形状和大小。(1)把圆规平放在桌面上,在圆规的两脚上各取一点A、C,自由转动其一个角,△ABC的形状、大小随之改变。那么还需增加什么条件就可以确定△ABC的形状、大小?ABCα④三个角3、给出三个元素③三条边②两角一边①两边一角两边夹角两边对角BC4cm5cm作图:画△ABC,使AB=4cm,AC=5cm ,∠A=45°。把所画的三角形剪下来与同桌所画的三角形进行比较,你发现了什么?A45° 三角形全等判定方法1用数学语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS)两边和它们的夹角对应相等的两个三角形全等。
简写成“边角边”或“SAS”。FEDCBAAC=DF
∠C=∠F
BC=EF∵ 例1、已知:如图,AD∥BC,AD=BC,求证:△ADC≌△CBA。证明:∵AD∥BC(已知)∴∠DAC=∠BCA(两直线平行,内错角相等)AD=BC(已知)∠DAC=∠BCA(已证)AC=CA(公共边)∴△ADC≌△CBA(SAS)练习1、已知:如图,AB=AC,AD=AE。
求证:(1)△ABE≌△ACD;
(2)∠B=∠C。(1)在△ABE和△ACD中AB=AC(已知)∠A=∠A(公共角)AE=AD(已知)∴△ABE≌△ACD(SAS)∵证明:(2)∵△ABE≌△ACD(已证)
∴∠B=∠C(全等三角形对应角相等)练习2、已知:如图,AC和BD相交于点O,OA=OC,OB=OD。
求证:AB∥DC 。证明:OA=OC(已知)∠AOB=∠COD (对顶角相等)OB=OD(已知)∴△ABO≌△CDO(SAS)∴∠A=∠C(全等三角形对应角相等)∴ AB∥DC(内错角相等,两直线平行) 可以得出:以后判定两条线段相等或两个角相等,还可以通过证明它们所在的两个三角形全等而得到。 ABCA’B’在岸上取可以直接到达A、B处的一点C,连结AC,延长至A′点,使A′C=AC;连结BC,并延长至B′点,使B′C=BC。连结A′B′, 量出的A′B′长,在△ABC和△A′B′C中AC=A′C(作图)∠ACB=∠A′CB ′(对顶角相等)BC=B′C(作图)∴△ABC≌△A′B′C(SAS)∴AB=A′B′(全等三角形对应边相等) 如图,在湖泊的岸边有A、B两点,难以直接量出A、B两点间的距离。你能设计一种量出A、B两点之间距离的方案吗?说明你这样设计的理由。∵ 小明要告诉师傅三角形的几个要素,才能使得新配的玻
璃和没打碎的三角形完全一样呢?2、在应用“SAS”时要注意:必须是对应的两边及两边
所夹的角相等。1、边角边定理:有两边和它们的夹角对应相等的两个三
角形全等(SAS)。3、今后判定两条线段相等或两个角相等可以通过证明它们
所在的两个三角形全等而得到。练习3、已知:如图,AB=DB,CB=EB, ∠1=∠2。
求证:∠A=∠D。∵ ∠1=∠2(已知)∴ ∠1+∠DBC= ∠2+∠DBC(等式性质)即∠ABC=∠DBE在△ABC和△DBE中AB=DB(已知)∠ABC=∠DBE(已证)CB=EB(已知)∴△ABC≌△DBE(SAS)∵证明: (2)如图,∠B、∠C已知,记两块三角尺的交点为A,沿直线l左右移动三角尺,△ABC的形状、大小随之改变,那么还需增加什么条件就可以确定△ABC的形状、大小呢?ABl结论:确定一个三角形的形状、大小至少需要三个元素。
第一课时
小明家里的柜子上镶有两块形状、大小完全一样的三角形玻
璃装饰板。其中的一块被打碎了,妈妈让他再去配一块一样
的。小明要告诉师傅三角形的几个要素,才能使得新配的玻
璃和没打碎的三角形完全一样呢?
④∠A=∠D ⑤∠B=∠E ⑥∠C=∠F 1、 什么叫全等三角形?能够完全重合的两个三角形叫全等三角形。2、 全等三角形有什么性质?△ABC≌△DEF①AB=DE ② BC=EF ③ CA=FD 全等三角形对应边相等,对应角相等。元素能不能尽可能的少呢?小明要告诉师傅三角形的几个要素,才能使得新
配的玻璃和没打碎的三角形完全一样呢?1.只给一个元素①只给一条边:②只给一个角:发现:只给一条边或一个角不能确定一个三角形的
形状和大小。2.给出两个元素①两边:②一边一内角:③两内角:发现;按这些条件画的三角形也都不能确定形状和大小。(1)把圆规平放在桌面上,在圆规的两脚上各取一点A、C,自由转动其一个角,△ABC的形状、大小随之改变。那么还需增加什么条件就可以确定△ABC的形状、大小?ABCα④三个角3、给出三个元素③三条边②两角一边①两边一角两边夹角两边对角BC4cm5cm作图:画△ABC,使AB=4cm,AC=5cm ,∠A=45°。把所画的三角形剪下来与同桌所画的三角形进行比较,你发现了什么?A45° 三角形全等判定方法1用数学语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS)两边和它们的夹角对应相等的两个三角形全等。
简写成“边角边”或“SAS”。FEDCBAAC=DF
∠C=∠F
BC=EF∵ 例1、已知:如图,AD∥BC,AD=BC,求证:△ADC≌△CBA。证明:∵AD∥BC(已知)∴∠DAC=∠BCA(两直线平行,内错角相等)AD=BC(已知)∠DAC=∠BCA(已证)AC=CA(公共边)∴△ADC≌△CBA(SAS)练习1、已知:如图,AB=AC,AD=AE。
求证:(1)△ABE≌△ACD;
(2)∠B=∠C。(1)在△ABE和△ACD中AB=AC(已知)∠A=∠A(公共角)AE=AD(已知)∴△ABE≌△ACD(SAS)∵证明:(2)∵△ABE≌△ACD(已证)
∴∠B=∠C(全等三角形对应角相等)练习2、已知:如图,AC和BD相交于点O,OA=OC,OB=OD。
求证:AB∥DC 。证明:OA=OC(已知)∠AOB=∠COD (对顶角相等)OB=OD(已知)∴△ABO≌△CDO(SAS)∴∠A=∠C(全等三角形对应角相等)∴ AB∥DC(内错角相等,两直线平行) 可以得出:以后判定两条线段相等或两个角相等,还可以通过证明它们所在的两个三角形全等而得到。 ABCA’B’在岸上取可以直接到达A、B处的一点C,连结AC,延长至A′点,使A′C=AC;连结BC,并延长至B′点,使B′C=BC。连结A′B′, 量出的A′B′长,在△ABC和△A′B′C中AC=A′C(作图)∠ACB=∠A′CB ′(对顶角相等)BC=B′C(作图)∴△ABC≌△A′B′C(SAS)∴AB=A′B′(全等三角形对应边相等) 如图,在湖泊的岸边有A、B两点,难以直接量出A、B两点间的距离。你能设计一种量出A、B两点之间距离的方案吗?说明你这样设计的理由。∵ 小明要告诉师傅三角形的几个要素,才能使得新配的玻
璃和没打碎的三角形完全一样呢?2、在应用“SAS”时要注意:必须是对应的两边及两边
所夹的角相等。1、边角边定理:有两边和它们的夹角对应相等的两个三
角形全等(SAS)。3、今后判定两条线段相等或两个角相等可以通过证明它们
所在的两个三角形全等而得到。练习3、已知:如图,AB=DB,CB=EB, ∠1=∠2。
求证:∠A=∠D。∵ ∠1=∠2(已知)∴ ∠1+∠DBC= ∠2+∠DBC(等式性质)即∠ABC=∠DBE在△ABC和△DBE中AB=DB(已知)∠ABC=∠DBE(已证)CB=EB(已知)∴△ABC≌△DBE(SAS)∵证明: (2)如图,∠B、∠C已知,记两块三角尺的交点为A,沿直线l左右移动三角尺,△ABC的形状、大小随之改变,那么还需增加什么条件就可以确定△ABC的形状、大小呢?ABl结论:确定一个三角形的形状、大小至少需要三个元素。
