2022-2023学年北师大版八年级数学下册 6.4 多边形的内角和与外角和 同步练习题 (无答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学下册 6.4 多边形的内角和与外角和 同步练习题 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 08:17:06 | ||
图片预览

文档简介
6.4 多边形的内角和与外角和 同步练习题2022-2023学年北师大版八年级数学下册
一、选择题
1.如图,四边形ABCD中,过点A的直线l将该四边形分割成两个多边形,若这两个多边形的内角和分别为α和β,则α+β= ( )
A.360° B.540° C.720° D.900°
2.如图,∠1=∠2=∠3=∠4=62°,分别作∠DEF和∠EFA的平分线,并交于点P,则∠P的度数是 ( )
A.55° B.56° C.57° D.60°
3.一个正多边形每个内角与每个外角的度数比为3∶1,则这个正多边形是 ( )
A.正方形 B.正六边形
C.正八边形 D.正十边形
4.如图,在正五边形ABCDE中,以AB为边向内作正△ABF,则下列结论错误的是 ( )
A.AE=AF B.∠EAF=∠CBF
C.∠F=∠EAF D.∠C=∠E
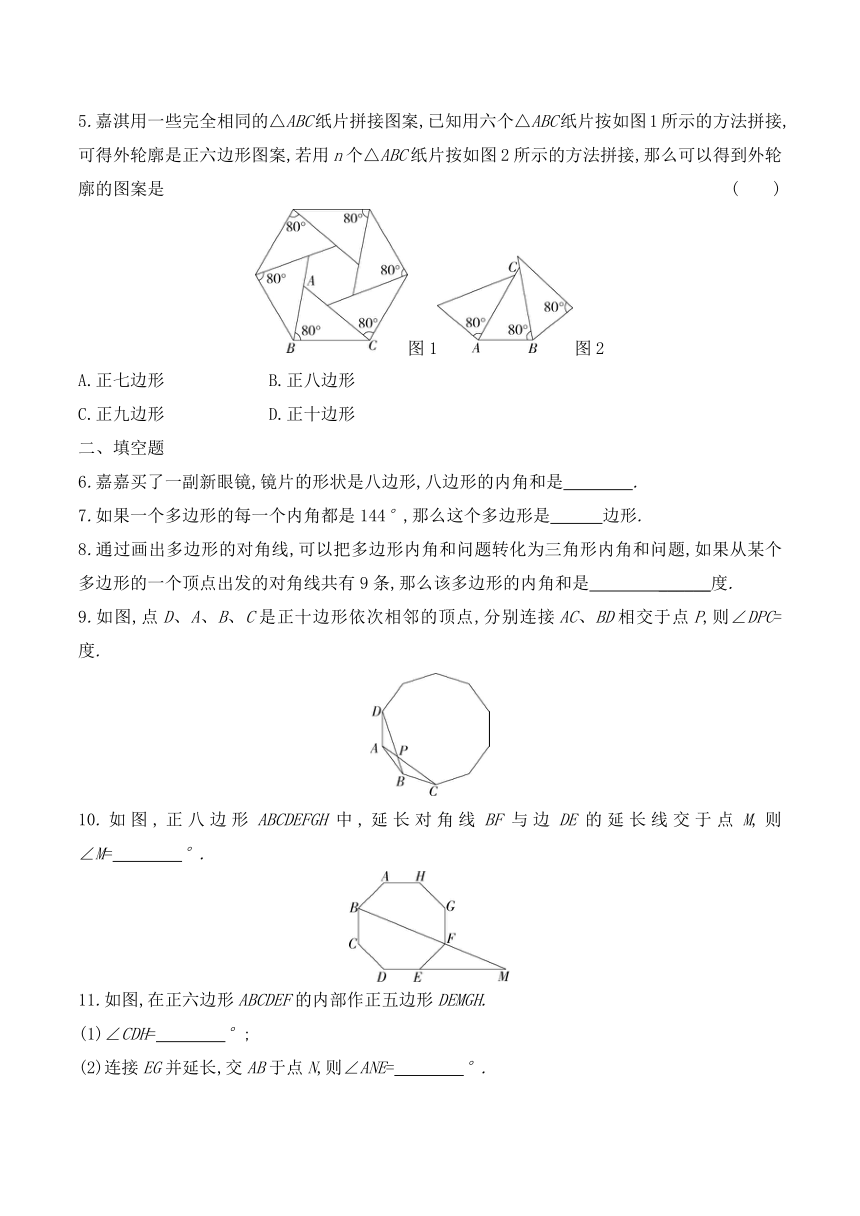
5.嘉淇用一些完全相同的△ABC纸片拼接图案,已知用六个△ABC纸片按如图1所示的方法拼接,可得外轮廓是正六边形图案,若用n个△ABC纸片按如图2所示的方法拼接,那么可以得到外轮廓的图案是 ( )
图1图2
A.正七边形 B.正八边形
C.正九边形 D.正十边形
二、填空题
6.嘉嘉买了一副新眼镜,镜片的形状是八边形,八边形的内角和是 .
7.如果一个多边形的每一个内角都是144°,那么这个多边形是 边形.
8.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从某个多边形的一个顶点出发的对角线共有9条,那么该多边形的内角和是 ______度.
9.如图,点D、A、B、C是正十边形依次相邻的顶点,分别连接AC、BD相交于点P,则∠DPC= 度.
10.如图,正八边形ABCDEFGH中,延长对角线BF与边DE的延长线交于点M,则∠M= °.
11.如图,在正六边形ABCDEF的内部作正五边形DEMGH.
(1)∠CDH= °;
(2)连接EG并延长,交AB于点N,则∠ANE= °.
12.在多边形中若各个内角度数之比是连续正整数,那么我们称这个多边形为“特质多边形”,例如度数之比为1∶2∶3的三角形就叫做“特质三角形”,1、2、3就是这个三角形的“特质数”.如果一个“特质三角形”有一个内角的度数是50°,那么这个三角形的“特质数”是_______.
三、解答题
13.若一个多边形的边数增加1,其内角和变为1440°,求原多边形的边数.
14.在各个内角都相等的多边形中,一个外角等于一个内角的,求这个多边形每一个内角的度数和它的边数.
15.小明和小亮分别利用图1、图2的不同方法求出了五边形的内角和都是540°.请你考虑在图3中再用另外一种方法求五边形的内角和.并写出求解过程.
16.如图1,图2,图3中,点E,D分别是正△ABC,正四边形ABCM,正五边形ABCMN中以C点为端点的相邻两边上的点,且BE=CD,DB交AE于P点.
(1)图1中,∠APD的度数为60°,图2中,∠APD的度数为90°,图3中,∠APD的度数为
_______(直接写出答案)
(2)根据前面探索,将本题推广到一般的正n边形情况.如图4,点E,D分别是正n边形ABCM
.…中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,求∠APD的度数.
17.如图,BE、DF分别平分四边形ABCD的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)试说明:∠MBC+∠NDC的度数与α,β的数量关系;
(2)如图1,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系;
(3)如图2,若α=β,判断BE和DF的位置关系,并说明理由.
图1图2
一、选择题
1.如图,四边形ABCD中,过点A的直线l将该四边形分割成两个多边形,若这两个多边形的内角和分别为α和β,则α+β= ( )
A.360° B.540° C.720° D.900°
2.如图,∠1=∠2=∠3=∠4=62°,分别作∠DEF和∠EFA的平分线,并交于点P,则∠P的度数是 ( )
A.55° B.56° C.57° D.60°
3.一个正多边形每个内角与每个外角的度数比为3∶1,则这个正多边形是 ( )
A.正方形 B.正六边形
C.正八边形 D.正十边形
4.如图,在正五边形ABCDE中,以AB为边向内作正△ABF,则下列结论错误的是 ( )
A.AE=AF B.∠EAF=∠CBF
C.∠F=∠EAF D.∠C=∠E
5.嘉淇用一些完全相同的△ABC纸片拼接图案,已知用六个△ABC纸片按如图1所示的方法拼接,可得外轮廓是正六边形图案,若用n个△ABC纸片按如图2所示的方法拼接,那么可以得到外轮廓的图案是 ( )
图1图2
A.正七边形 B.正八边形
C.正九边形 D.正十边形
二、填空题
6.嘉嘉买了一副新眼镜,镜片的形状是八边形,八边形的内角和是 .
7.如果一个多边形的每一个内角都是144°,那么这个多边形是 边形.
8.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从某个多边形的一个顶点出发的对角线共有9条,那么该多边形的内角和是 ______度.
9.如图,点D、A、B、C是正十边形依次相邻的顶点,分别连接AC、BD相交于点P,则∠DPC= 度.
10.如图,正八边形ABCDEFGH中,延长对角线BF与边DE的延长线交于点M,则∠M= °.
11.如图,在正六边形ABCDEF的内部作正五边形DEMGH.
(1)∠CDH= °;
(2)连接EG并延长,交AB于点N,则∠ANE= °.
12.在多边形中若各个内角度数之比是连续正整数,那么我们称这个多边形为“特质多边形”,例如度数之比为1∶2∶3的三角形就叫做“特质三角形”,1、2、3就是这个三角形的“特质数”.如果一个“特质三角形”有一个内角的度数是50°,那么这个三角形的“特质数”是_______.
三、解答题
13.若一个多边形的边数增加1,其内角和变为1440°,求原多边形的边数.
14.在各个内角都相等的多边形中,一个外角等于一个内角的,求这个多边形每一个内角的度数和它的边数.
15.小明和小亮分别利用图1、图2的不同方法求出了五边形的内角和都是540°.请你考虑在图3中再用另外一种方法求五边形的内角和.并写出求解过程.
16.如图1,图2,图3中,点E,D分别是正△ABC,正四边形ABCM,正五边形ABCMN中以C点为端点的相邻两边上的点,且BE=CD,DB交AE于P点.
(1)图1中,∠APD的度数为60°,图2中,∠APD的度数为90°,图3中,∠APD的度数为
_______(直接写出答案)
(2)根据前面探索,将本题推广到一般的正n边形情况.如图4,点E,D分别是正n边形ABCM
.…中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,求∠APD的度数.
17.如图,BE、DF分别平分四边形ABCD的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)试说明:∠MBC+∠NDC的度数与α,β的数量关系;
(2)如图1,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系;
(3)如图2,若α=β,判断BE和DF的位置关系,并说明理由.
图1图2
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
