2022-2023学年北师大版八年级数学下册 第六章 平行四边形 单元习题 (含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学下册 第六章 平行四边形 单元习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 08:19:40 | ||
图片预览



文档简介
第六章 平行四边形 同步练习题2022-2023学年北师大版八年级数学下册
一、选择题(每小题3分,共30分)
1.在 ABCD中,若AB=3,BC=5,则 ABCD的周长是 ( )
A.8 B.16 C.11 D.13
2.正多边形的每个内角为108°,则它的边数是 ( )
A.4 B.6 C.7 D.5
3.如图,在 ABCD中,连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
A.80° B.100° C.120° D.140°
4.关于四边形ABCD有以下几个条件:①两组对边分别平行;②两组对边分别相等;③有两组角相等;④对角线AC和BD相等.其中可以判定四边形ABCD是平行四边形的有( )
A.1个 B.2个 C.3个 D.4个
5.若平行四边形的一条边长为9,则它的两条对角线长可能是( )
A.3和4 B.5和6 C.6和8 D.10和12
6.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了其中两块碎玻璃,其编号应该是 ( )
A.①③ B.①② C.③④ D.②④
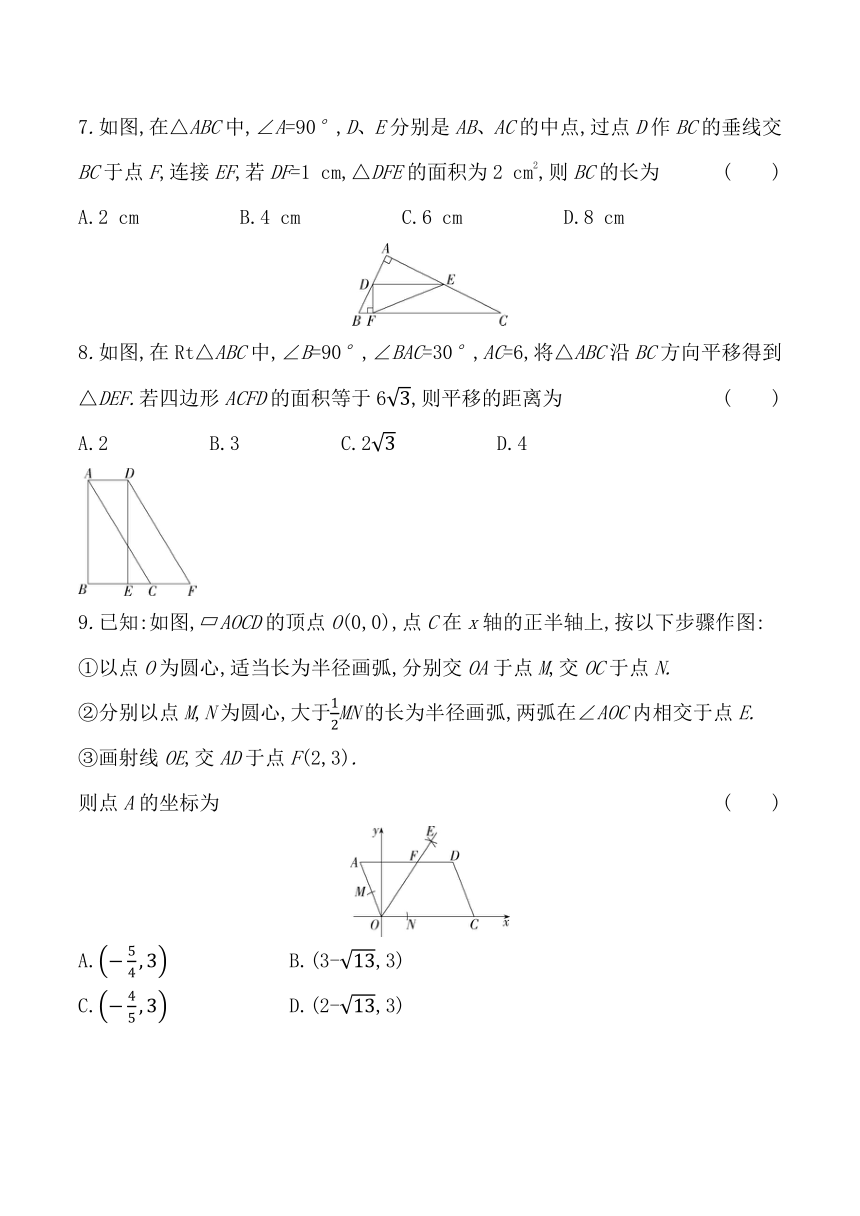
7.如图,在△ABC中,∠A=90°,D、E分别是AB、AC的中点,过点D作BC的垂线交BC于点F,连接EF,若DF=1 cm,△DFE的面积为2 cm2,则BC的长为 ( )
A.2 cm B.4 cm C.6 cm D.8 cm
8.如图,在Rt△ABC中,∠B=90°,∠BAC=30°,AC=6,将△ABC沿BC方向平移得到△DEF.若四边形ACFD的面积等于6,则平移的距离为 ( )
A.2 B.3 C.2 D.4
9.已知:如图, AOCD的顶点O(0,0),点C在x轴的正半轴上,按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3).
则点A的坐标为 ( )
A. B.(3-,3)
C. D.(2-,3)
10.如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE和等边△ADF,延长CB交AE于点G,连接CE、CF、EF,则以下四个结论:①△CDF≌△EBC;②∠CDF=∠EAF;
③CG⊥AE;④△CEF是等边三角形,正确的是 ( )
A.③④ B.①②④ C.①②③ D.①②③④
二、填空题(每小题4分,共28分)
11.一种多边形的零配件,测得它的每一个外角都等于40°,则这个多边形的边数是 .
12.如图,点D、E、F分别为△ABC三边的中点.若△ABC的周长为10,则△DEF的周长为 .
13.如图, ABCD的对角线AC,BD相交于点O,若△AOB的面积为6 cm2,则 ABCD的面积为 .
14.如图所示的是由在同一平面内的9个平行四边形组成的立体视觉效果图.若∠1=60°,∠2=130°,则∠3= °.
15.如图,一束太阳光线平行照射在放置于地面的正六边形上,若∠1=19°,则∠2的度数为 .
16.在平行四边形ABCD中,∠A=30°,AD=4,BD=4,则平行四边形ABCD的面积等于 .
17.在平面直角坐标系中,A(-1,1),B(2,3),C(m,2m+1),D在x轴上,若以A,B,C,D四点为顶点的四边形是平行四边形,则点D的坐标为 .
三、解答题(共42分)
18.(6分)看图回答问题:
(1)内角和为2 014°,小明为什么说不可能
(2)小华求的是几边形的内角和
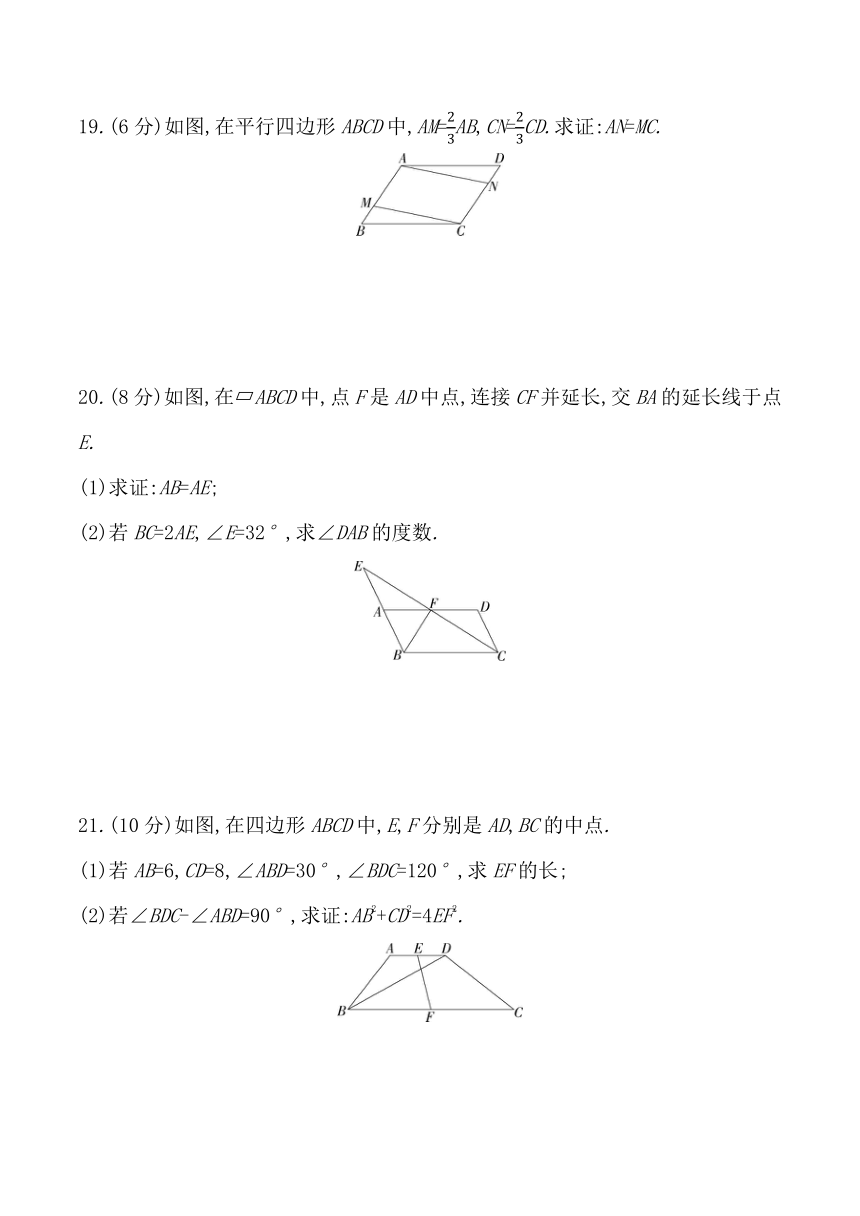
19.(6分)如图,在平行四边形ABCD中,AM=AB,CN=CD.求证:AN=MC.
20.(8分)如图,在 ABCD中,点F是AD中点,连接CF并延长,交BA的延长线于点E.
(1)求证:AB=AE;
(2)若BC=2AE,∠E=32°,求∠DAB的度数.
21.(10分)如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC-∠ABD=90°,求证:AB2+CD2=4EF2.
22.(12分)如图①所示,四边形MNBD为一张长方形纸片.如图②所示,将长方形纸片剪两刀,剪出三个角(∠BAE、∠AEC、∠ECD),则∠BAE+∠AEC+∠ECD= .
(1)如图③所示,将长方形纸片剪三刀,剪出四个角(∠BAE、∠AEF、∠EFC、∠FCD),则∠BAE+∠AEF+∠EFC+∠FCD= ;
(2)如图④所示,将长方形纸片剪四刀,剪出五个角(∠BAE、∠AEF、∠EFG、∠FGC、∠GCD),则∠BAE+∠AEF+∠EFG+∠FGC+∠GCD= ;
(3)根据前面的探索规律,将长方形纸片按照上述剪法剪n刀,剪出(n+1)个角,那么这(n+1)个角的和是 .
图①
图②
图③
图④
参考答案
1.B ∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴ ABCD的周长为2(AB+BC)=16.
故选B.
2.D ∵正多边形的每个内角等于108°,
∴这个多边形的每个外角的度数为180°-108°=72°,
∴这个多边形的边数=360°÷72°=5,
故选D.
3.C ∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠DCA=∠CAB=40°,
∵∠BCD=∠DCA+∠ACB,
∴∠BCD=40°+80°=120°,
故选C.
4.B ①是平行四边形的定义,②是平行四边形的判定定理,③④不能判定四边形ABCD是平行四边形.故选B.
5.D A.3÷2=1.5,4÷2=2,2+1.5=3.5<9,故不能构成三角形,故本选项不符合题意;
B.5÷2=2.5,6÷2=3,2.5+3=5.5<9,故不能构成三角形,故本选项不符合题意;
C.6÷2=3,8÷2=4,3+4=7<9,故不能构成三角形,故本选项不符合题意;
D.10÷2=5,12÷2=6,5+6=11>9,符合三角形的三边关系,能构成三角形,故本选项符合题意.
故选D.
6.A 由题图易知带①③两块碎玻璃,可以在商店配到一块与原来相同的平行四边形玻璃,故选A.
7.D ∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∵∠DFB=90°,
∴∠FDE=∠DFB=90°,
∵△DFE的面积为2 cm2,
∴DE·DF=2 cm2,
∵DF=1 cm,∴DE=4 cm,
∴BC=2DE=8 cm.故选D.
8.A ∵∠B=90°,∠BAC=30°,AC=6,
∴BC=AC=3,∴AB===3,
∵将△ABC沿BC方向平移得到△DEF,
∴AD=CF,AD∥CF,∴四边形ACFD是平行四边形,
∵四边形ACFD的面积等于6,
∴CF·AB=6,∴CF=2,∴平移的距离为2.故选A.
9.A 如图,设AD与y轴交于点H,由作图步骤可知OE平分∠AOC,
∴∠AOF=∠COF,
∵在 AOCD中,AD∥OC,
∴∠COF=∠AFO,
∴∠AOF=∠AFO,∴AO=AF,
∵F(2,3),∴FH=2,OH=3,
设AH=m,则AO=AF=2+m,
∵在Rt△AOH中,AH2+OH2=AO2,
∴m2+32=(2+m) 2,解得m=,∴A,
故选A.
10.B ∵△ABE、△ADF是等边三角形,∴FD=AD,BE=AB,
∵AD=BC,AB=DC,∴FD=BC,BE=DC,
∵∠CBA=∠ADC,∠ABE=∠FDA,∴∠EBC=∠CDF,
∴△EBC≌△CDF(SAS),故①正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°-∠CDA)=300°-∠CDA,∠FDC=360°-∠FDA-∠ADC=300°-∠CDA,
∴∠CDF=∠EAF,故②正确;
由已知不能得到CG⊥AE,故③错误;
由①②可得∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC(SAS),
∴∠AEF=∠BEC,FE=CE,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,∴△ECF是等边三角形,故④正确.
故选B.
11.答案 9
解析 ∵360°÷40°=9,
∴这个多边形的边数是9.故答案为9.
12.答案 5
解析 ∵D、E、F分别是AB、AC、BC的中点,
∴FD、FE、DE均为△ABC的中位线,
∴DF=AC,FE=AB,DE=BC,
∴△DEF的周长=DF+FE+DE=AC+AB+BC=(AC+AB+BC)=×10=5.
13.答案 24 cm2
解析 在 ABCD中,OA=OC,OB=OD,AB=CD,
∴△AOB≌△COD,∴S△COD=S△AOB=6 cm2.
∵OA=OC,∴S△BOC=S△AOB=6 cm2.
同理,S△AOD=S△AOB=6 cm2,
∴S ABCD=4×6=24 cm2.
14.答案 110
解析 如图,
∵四边形ADEF是平行四边形,∠2=130°,
∴∠ADE=∠2=130°,
∵∠1=60°,
∴∠DAB=∠1=60°,
∵四边形ABCD是平行四边形,
∴∠DAB+∠ADC=180°,
∴∠ADC=180°-∠DAB=180°-60°=120°,
∴∠3=360°-∠ADE-∠ADC=360°-130°-120°=110°,故答案为110.
15.答案 41°
解析 如图,∵正六边形的每个内角都等于120°,每个外角都等于60°,
∴∠FAD=120°-∠1=101°,∠ADB=60°,
∴∠ABD=101°-60°=41°.
∵光线是平行的,∴∠2=∠ABD=41°.
16.答案 16或8
解析 过点D作DE⊥直线AB于E,∵∠A=30°,
∴DE=AD=2,
∴AE===6.
在Rt△DBE中,BE===2.
当E在线段AB上时,如图①,此时AB=AE+BE=8,
∴S ABCD=AB·DE=8×2=16;
当E在线段AB的延长线上时,如图②,此时AB=AE-BE=4,∴S ABCD=AB·DE=4×2=8.
图①
图②
综上,平行四边形ABCD的面积等于16或8.
17.答案 或
解析 设D(n,0),
∵A(-1,1),B(2,3),C(m,2m+1),
∴根据以A,B,C,D四点为顶点的四边形是平行四边形可得,
①若四边形ABCD为平行四边形,
则解得
∴D,
易知此时A,B,C,D四点共线,
∴此种情况不满足题意;
②若四边形ADBC为平行四边形,
则解得
∴D;
③若四边形ABDC为平行四边形,
则解得
∴D.
综上,点D的坐标为或.
故答案为或.
18.解析 (1)∵n边形的内角和是(n-2)·180°,n为大于或等于3的整数,
∴凸多边形的内角和一定是180度的整数倍,
∵2 014÷180=11……34,
∴内角和不可能为2 014°.
(2)设该多边形的边数为x,依题意有(x-2)·180°<2 014°,解得x<13.
∵x为大于或等于3的整数且多加的外角度数一定小于180°,∴多边形的边数是13,
故小华求的是十三边形的内角和.
19.证明 ∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∵AM=AB,CN=CD,∴AM=NC,
∵AM∥NC,∴四边形AMCN是平行四边形,
∴AN=MC.
20.解析 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∴∠E=∠DCF,
∵点F是AD中点,∴AF=DF,
在△AFE和△DFC中,
∴△AFE≌△DFC(AAS),∴CD=AE,
∵AB=CD,∴AB=AE.
(2)由(1)可得AF=DF,
∵四边形ABCD是平行四边形,∴BC=AD,∴BC=2AF,
∵BC=2AE,∴AE=AF,
∵∠E=32°,∴∠AFE=∠E=32°,∴∠DAB=2∠E=64°.
21.解析 (1)取BD的中点P,连接EP、FP(图略).
∵E,F分别是AD,BC的中点,AB=6,CD=8,
∴PE∥AB且PE=AB=3,PF∥CD且PF=CD=4.
又∵∠ABD=30°,∠BDC=120°,
∴∠EPD=∠ABD=30°,∠DPF=180°-∠BDC=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在Rt△EPF中,由勾股定理得EF===5,即EF=5.
(2)证明:取BD的中点P,连接EP、FP(图略).
∵E,F分别是AD,BC的中点,
∴PE∥AB且PE=AB,PF∥CD且PF=CD,
∴∠EPD=∠ABD,∠BPF=∠BDC,
∴∠DPF=180°-∠BPF=180°-∠BDC,
∵∠BDC-∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°-∠BDC=∠ABD+180°-(90°+∠ABD)=90°,
∴PE2+PF2=+=EF2,
∴AB2+CD2=4EF2.
22.解析 过E作EF∥AB,如图1.
∵原四边形是长方形,
∴AB∥CD,
又∵EF∥AB,∴CD∥EF(平行于同一条直线的两条直线互相平行).
∵EF∥AB,∴∠BAE+∠1=180°(两直线平行,同旁内角互补).
∵CD∥EF,
∴∠2+∠ECD=180°(两直线平行,同旁内角互补).
∴∠BAE+∠1+∠2+∠ECD=360°,
又∵∠1+∠2=∠AEC,
∴∠BAE+∠AEC+∠ECD=360°.
图1
(1)过E、F分别作AB的平行线,如图2所示,
图2
用上述方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°.
(2)过E、F、G分别作AB的平行线,如图3所示,
图3
用上述方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°.
(3)由上述规律可得剪n刀,剪出(n+1)个角,那么这(n+1)个角的和是n·180°.
一、选择题(每小题3分,共30分)
1.在 ABCD中,若AB=3,BC=5,则 ABCD的周长是 ( )
A.8 B.16 C.11 D.13
2.正多边形的每个内角为108°,则它的边数是 ( )
A.4 B.6 C.7 D.5
3.如图,在 ABCD中,连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
A.80° B.100° C.120° D.140°
4.关于四边形ABCD有以下几个条件:①两组对边分别平行;②两组对边分别相等;③有两组角相等;④对角线AC和BD相等.其中可以判定四边形ABCD是平行四边形的有( )
A.1个 B.2个 C.3个 D.4个
5.若平行四边形的一条边长为9,则它的两条对角线长可能是( )
A.3和4 B.5和6 C.6和8 D.10和12
6.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了其中两块碎玻璃,其编号应该是 ( )
A.①③ B.①② C.③④ D.②④
7.如图,在△ABC中,∠A=90°,D、E分别是AB、AC的中点,过点D作BC的垂线交BC于点F,连接EF,若DF=1 cm,△DFE的面积为2 cm2,则BC的长为 ( )
A.2 cm B.4 cm C.6 cm D.8 cm
8.如图,在Rt△ABC中,∠B=90°,∠BAC=30°,AC=6,将△ABC沿BC方向平移得到△DEF.若四边形ACFD的面积等于6,则平移的距离为 ( )
A.2 B.3 C.2 D.4
9.已知:如图, AOCD的顶点O(0,0),点C在x轴的正半轴上,按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3).
则点A的坐标为 ( )
A. B.(3-,3)
C. D.(2-,3)
10.如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE和等边△ADF,延长CB交AE于点G,连接CE、CF、EF,则以下四个结论:①△CDF≌△EBC;②∠CDF=∠EAF;
③CG⊥AE;④△CEF是等边三角形,正确的是 ( )
A.③④ B.①②④ C.①②③ D.①②③④
二、填空题(每小题4分,共28分)
11.一种多边形的零配件,测得它的每一个外角都等于40°,则这个多边形的边数是 .
12.如图,点D、E、F分别为△ABC三边的中点.若△ABC的周长为10,则△DEF的周长为 .
13.如图, ABCD的对角线AC,BD相交于点O,若△AOB的面积为6 cm2,则 ABCD的面积为 .
14.如图所示的是由在同一平面内的9个平行四边形组成的立体视觉效果图.若∠1=60°,∠2=130°,则∠3= °.
15.如图,一束太阳光线平行照射在放置于地面的正六边形上,若∠1=19°,则∠2的度数为 .
16.在平行四边形ABCD中,∠A=30°,AD=4,BD=4,则平行四边形ABCD的面积等于 .
17.在平面直角坐标系中,A(-1,1),B(2,3),C(m,2m+1),D在x轴上,若以A,B,C,D四点为顶点的四边形是平行四边形,则点D的坐标为 .
三、解答题(共42分)
18.(6分)看图回答问题:
(1)内角和为2 014°,小明为什么说不可能
(2)小华求的是几边形的内角和
19.(6分)如图,在平行四边形ABCD中,AM=AB,CN=CD.求证:AN=MC.
20.(8分)如图,在 ABCD中,点F是AD中点,连接CF并延长,交BA的延长线于点E.
(1)求证:AB=AE;
(2)若BC=2AE,∠E=32°,求∠DAB的度数.
21.(10分)如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC-∠ABD=90°,求证:AB2+CD2=4EF2.
22.(12分)如图①所示,四边形MNBD为一张长方形纸片.如图②所示,将长方形纸片剪两刀,剪出三个角(∠BAE、∠AEC、∠ECD),则∠BAE+∠AEC+∠ECD= .
(1)如图③所示,将长方形纸片剪三刀,剪出四个角(∠BAE、∠AEF、∠EFC、∠FCD),则∠BAE+∠AEF+∠EFC+∠FCD= ;
(2)如图④所示,将长方形纸片剪四刀,剪出五个角(∠BAE、∠AEF、∠EFG、∠FGC、∠GCD),则∠BAE+∠AEF+∠EFG+∠FGC+∠GCD= ;
(3)根据前面的探索规律,将长方形纸片按照上述剪法剪n刀,剪出(n+1)个角,那么这(n+1)个角的和是 .
图①
图②
图③
图④
参考答案
1.B ∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴ ABCD的周长为2(AB+BC)=16.
故选B.
2.D ∵正多边形的每个内角等于108°,
∴这个多边形的每个外角的度数为180°-108°=72°,
∴这个多边形的边数=360°÷72°=5,
故选D.
3.C ∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠DCA=∠CAB=40°,
∵∠BCD=∠DCA+∠ACB,
∴∠BCD=40°+80°=120°,
故选C.
4.B ①是平行四边形的定义,②是平行四边形的判定定理,③④不能判定四边形ABCD是平行四边形.故选B.
5.D A.3÷2=1.5,4÷2=2,2+1.5=3.5<9,故不能构成三角形,故本选项不符合题意;
B.5÷2=2.5,6÷2=3,2.5+3=5.5<9,故不能构成三角形,故本选项不符合题意;
C.6÷2=3,8÷2=4,3+4=7<9,故不能构成三角形,故本选项不符合题意;
D.10÷2=5,12÷2=6,5+6=11>9,符合三角形的三边关系,能构成三角形,故本选项符合题意.
故选D.
6.A 由题图易知带①③两块碎玻璃,可以在商店配到一块与原来相同的平行四边形玻璃,故选A.
7.D ∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∵∠DFB=90°,
∴∠FDE=∠DFB=90°,
∵△DFE的面积为2 cm2,
∴DE·DF=2 cm2,
∵DF=1 cm,∴DE=4 cm,
∴BC=2DE=8 cm.故选D.
8.A ∵∠B=90°,∠BAC=30°,AC=6,
∴BC=AC=3,∴AB===3,
∵将△ABC沿BC方向平移得到△DEF,
∴AD=CF,AD∥CF,∴四边形ACFD是平行四边形,
∵四边形ACFD的面积等于6,
∴CF·AB=6,∴CF=2,∴平移的距离为2.故选A.
9.A 如图,设AD与y轴交于点H,由作图步骤可知OE平分∠AOC,
∴∠AOF=∠COF,
∵在 AOCD中,AD∥OC,
∴∠COF=∠AFO,
∴∠AOF=∠AFO,∴AO=AF,
∵F(2,3),∴FH=2,OH=3,
设AH=m,则AO=AF=2+m,
∵在Rt△AOH中,AH2+OH2=AO2,
∴m2+32=(2+m) 2,解得m=,∴A,
故选A.
10.B ∵△ABE、△ADF是等边三角形,∴FD=AD,BE=AB,
∵AD=BC,AB=DC,∴FD=BC,BE=DC,
∵∠CBA=∠ADC,∠ABE=∠FDA,∴∠EBC=∠CDF,
∴△EBC≌△CDF(SAS),故①正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°-∠CDA)=300°-∠CDA,∠FDC=360°-∠FDA-∠ADC=300°-∠CDA,
∴∠CDF=∠EAF,故②正确;
由已知不能得到CG⊥AE,故③错误;
由①②可得∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC(SAS),
∴∠AEF=∠BEC,FE=CE,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,∴△ECF是等边三角形,故④正确.
故选B.
11.答案 9
解析 ∵360°÷40°=9,
∴这个多边形的边数是9.故答案为9.
12.答案 5
解析 ∵D、E、F分别是AB、AC、BC的中点,
∴FD、FE、DE均为△ABC的中位线,
∴DF=AC,FE=AB,DE=BC,
∴△DEF的周长=DF+FE+DE=AC+AB+BC=(AC+AB+BC)=×10=5.
13.答案 24 cm2
解析 在 ABCD中,OA=OC,OB=OD,AB=CD,
∴△AOB≌△COD,∴S△COD=S△AOB=6 cm2.
∵OA=OC,∴S△BOC=S△AOB=6 cm2.
同理,S△AOD=S△AOB=6 cm2,
∴S ABCD=4×6=24 cm2.
14.答案 110
解析 如图,
∵四边形ADEF是平行四边形,∠2=130°,
∴∠ADE=∠2=130°,
∵∠1=60°,
∴∠DAB=∠1=60°,
∵四边形ABCD是平行四边形,
∴∠DAB+∠ADC=180°,
∴∠ADC=180°-∠DAB=180°-60°=120°,
∴∠3=360°-∠ADE-∠ADC=360°-130°-120°=110°,故答案为110.
15.答案 41°
解析 如图,∵正六边形的每个内角都等于120°,每个外角都等于60°,
∴∠FAD=120°-∠1=101°,∠ADB=60°,
∴∠ABD=101°-60°=41°.
∵光线是平行的,∴∠2=∠ABD=41°.
16.答案 16或8
解析 过点D作DE⊥直线AB于E,∵∠A=30°,
∴DE=AD=2,
∴AE===6.
在Rt△DBE中,BE===2.
当E在线段AB上时,如图①,此时AB=AE+BE=8,
∴S ABCD=AB·DE=8×2=16;
当E在线段AB的延长线上时,如图②,此时AB=AE-BE=4,∴S ABCD=AB·DE=4×2=8.
图①
图②
综上,平行四边形ABCD的面积等于16或8.
17.答案 或
解析 设D(n,0),
∵A(-1,1),B(2,3),C(m,2m+1),
∴根据以A,B,C,D四点为顶点的四边形是平行四边形可得,
①若四边形ABCD为平行四边形,
则解得
∴D,
易知此时A,B,C,D四点共线,
∴此种情况不满足题意;
②若四边形ADBC为平行四边形,
则解得
∴D;
③若四边形ABDC为平行四边形,
则解得
∴D.
综上,点D的坐标为或.
故答案为或.
18.解析 (1)∵n边形的内角和是(n-2)·180°,n为大于或等于3的整数,
∴凸多边形的内角和一定是180度的整数倍,
∵2 014÷180=11……34,
∴内角和不可能为2 014°.
(2)设该多边形的边数为x,依题意有(x-2)·180°<2 014°,解得x<13.
∵x为大于或等于3的整数且多加的外角度数一定小于180°,∴多边形的边数是13,
故小华求的是十三边形的内角和.
19.证明 ∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∵AM=AB,CN=CD,∴AM=NC,
∵AM∥NC,∴四边形AMCN是平行四边形,
∴AN=MC.
20.解析 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∴∠E=∠DCF,
∵点F是AD中点,∴AF=DF,
在△AFE和△DFC中,
∴△AFE≌△DFC(AAS),∴CD=AE,
∵AB=CD,∴AB=AE.
(2)由(1)可得AF=DF,
∵四边形ABCD是平行四边形,∴BC=AD,∴BC=2AF,
∵BC=2AE,∴AE=AF,
∵∠E=32°,∴∠AFE=∠E=32°,∴∠DAB=2∠E=64°.
21.解析 (1)取BD的中点P,连接EP、FP(图略).
∵E,F分别是AD,BC的中点,AB=6,CD=8,
∴PE∥AB且PE=AB=3,PF∥CD且PF=CD=4.
又∵∠ABD=30°,∠BDC=120°,
∴∠EPD=∠ABD=30°,∠DPF=180°-∠BDC=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在Rt△EPF中,由勾股定理得EF===5,即EF=5.
(2)证明:取BD的中点P,连接EP、FP(图略).
∵E,F分别是AD,BC的中点,
∴PE∥AB且PE=AB,PF∥CD且PF=CD,
∴∠EPD=∠ABD,∠BPF=∠BDC,
∴∠DPF=180°-∠BPF=180°-∠BDC,
∵∠BDC-∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°-∠BDC=∠ABD+180°-(90°+∠ABD)=90°,
∴PE2+PF2=+=EF2,
∴AB2+CD2=4EF2.
22.解析 过E作EF∥AB,如图1.
∵原四边形是长方形,
∴AB∥CD,
又∵EF∥AB,∴CD∥EF(平行于同一条直线的两条直线互相平行).
∵EF∥AB,∴∠BAE+∠1=180°(两直线平行,同旁内角互补).
∵CD∥EF,
∴∠2+∠ECD=180°(两直线平行,同旁内角互补).
∴∠BAE+∠1+∠2+∠ECD=360°,
又∵∠1+∠2=∠AEC,
∴∠BAE+∠AEC+∠ECD=360°.
图1
(1)过E、F分别作AB的平行线,如图2所示,
图2
用上述方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°.
(2)过E、F、G分别作AB的平行线,如图3所示,
图3
用上述方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°.
(3)由上述规律可得剪n刀,剪出(n+1)个角,那么这(n+1)个角的和是n·180°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
