28.2解直角三角形同步练习
文档属性
| 名称 | 28.2解直角三角形同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 131.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-25 00:00:00 | ||
图片预览


文档简介
解直角三角形同步练习
一、填空题:
1.在△ABC中,C=90°,若=1,sinA=,则= .
2.旗杆的上一段BC被风吹断(C处仍连接),顶端着地与地面成30°角,顶端着地处B与旗杆底端相距4米,则旗杆原来高度为_________米. (结果保留根号)
3.已知直角三角形的两直角边的比为3:4,则最小角度数为_______°.(精确到0.1度)
4.已知△ABC的周长为4+2,则BC= .
5.利用计算器求值(保留4位有效数字):cos75°12′= ; 44°13′= .
6.伽利略曾用“比萨斜塔”进行重力定律实验.他从55米长的塔顶让一重物自由下落,物体的着地点离塔底4.8米,斜塔偏离铅垂线的角度是 °(精确到0.1度)
7.一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A测得某灯塔位于它的北偏东30°的B处(如图1).上午九时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里.(结果保留根号)
8.若一个等腰三角形的两边长分别为2cm和6cm,则底边上的高为__________cm,底角的度数是__________(精确到0.1度).
9.小强和小明去测量一座古塔的高度(如图2),他们在离古塔60米的A处,用测角仪测得古塔塔顶的仰角为32°,已知测角仪器高AD=1米,则古塔BE的高度为_______米.(精确到0.1米)
10.在Rt△ABC中,∠C=90°,,,则a=__________,b=__________,=__________.
11.如图,一护栏AB被一钢缆CD固定,CD与地面成25°36’的角,且DB=5,现再在C点上方2处加固另一钢缆ED,那么∠EDC=___________.(精确到分)
12.如图4,从楼顶A点测得电视塔CD的仰角为α,俯角为β,若楼房与电视塔之间的水平距离为m,则电视塔的高度CD是__________.
第7题 第9题 第11题 第12题
二、选择题:
13.在Rt△ABC中,∠C=90°,cosA=,=,则等于( ).
A.1 B. C.2 D.3
14.已知A=1.7321,锐角A=( ).
A. 60° B.58° C.40° D. 10°
15.甲、乙、丙三人放风筝,各人放出的风筝线长分别为60m、50m、40m,线与地平面所成的角分别为30o、45o、60o,假设风筝线近似看作是拉直的,则所放风筝最高的是( ).
A.甲 B.乙 C.丙 D.不能确定
16.如图5,为了测量河两岸的A、B两点间的距离,在与AB垂直的方向上取点C,测得AC=a,∠ACB=α,则AB的长为 ( ).
A. B. C. D.
17.如图6,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为( ).
A. 1 B. C. D.
18.在Rt△ABC中,∠B=90°,∠ACB=45°,点D在BC的延长线上,且CD=CA,则和tan22°30′的值相等的是( ).
A. B. C. D.
19.如图7,水库大坝的横断面是梯形,坝顶宽6,坝高24,斜坡的坡角为,斜坡的坡角D的正切值为,则坡底AD的长为( ).
A. B.42 C. D.
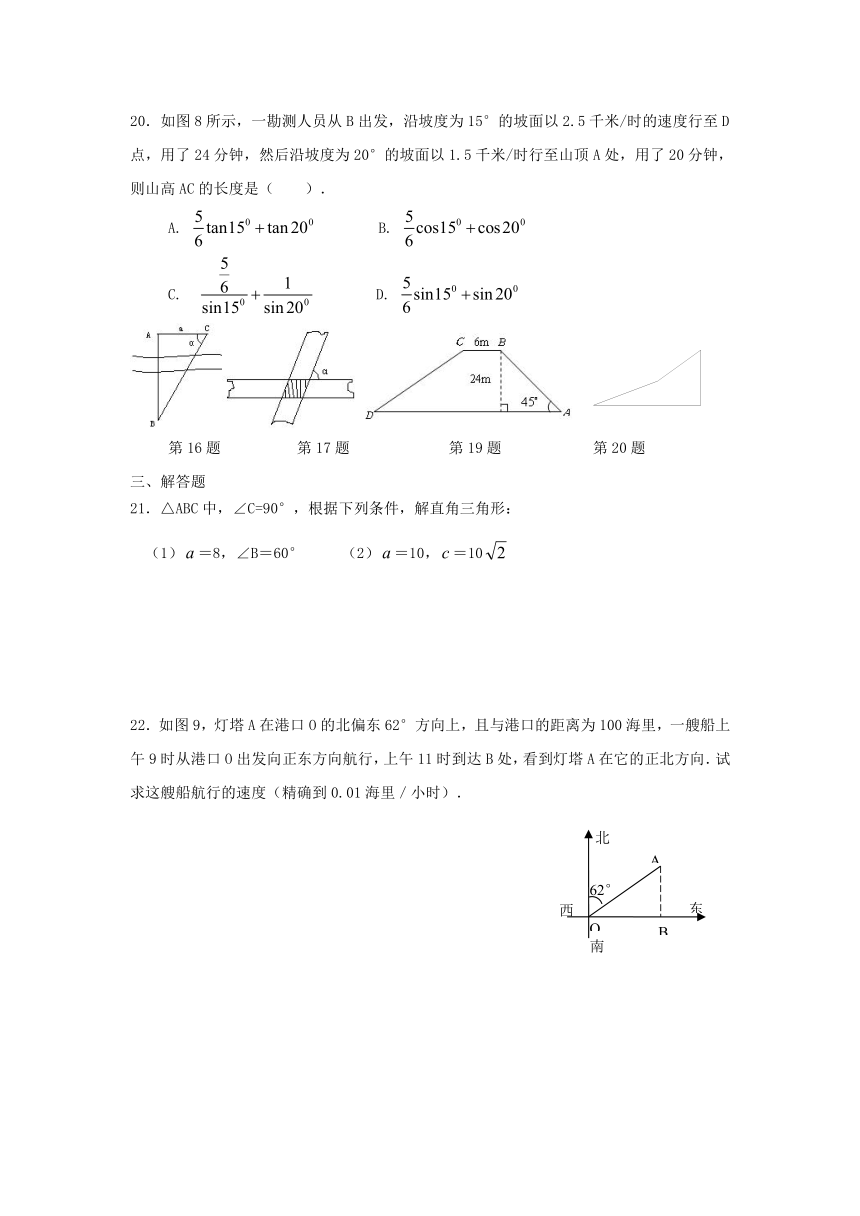
20.如图8所示,一勘测人员从B出发,沿坡度为15°的坡面以2.5千米/时的速度行至D点,用了24分钟,然后沿坡度为20°的坡面以1.5千米/时行至山顶A处,用了20分钟,则山高AC的长度是( ).
A. B.
C. D.
第16题 第17题 第19题 第20题
三、解答题
21.△ABC中,∠C=90°,根据下列条件,解直角三角形:
(1)=8,∠B=60° (2)=10,=10
22.如图9,灯塔A在港口O的北偏东62°方向上,且与港口的距离为100海里,一艘船上午9时从港口O出发向正东方向航行,上午11时到达B处,看到灯塔A在它的正北方向.试求这艘船航行的速度(精确到0.01海里/小时).
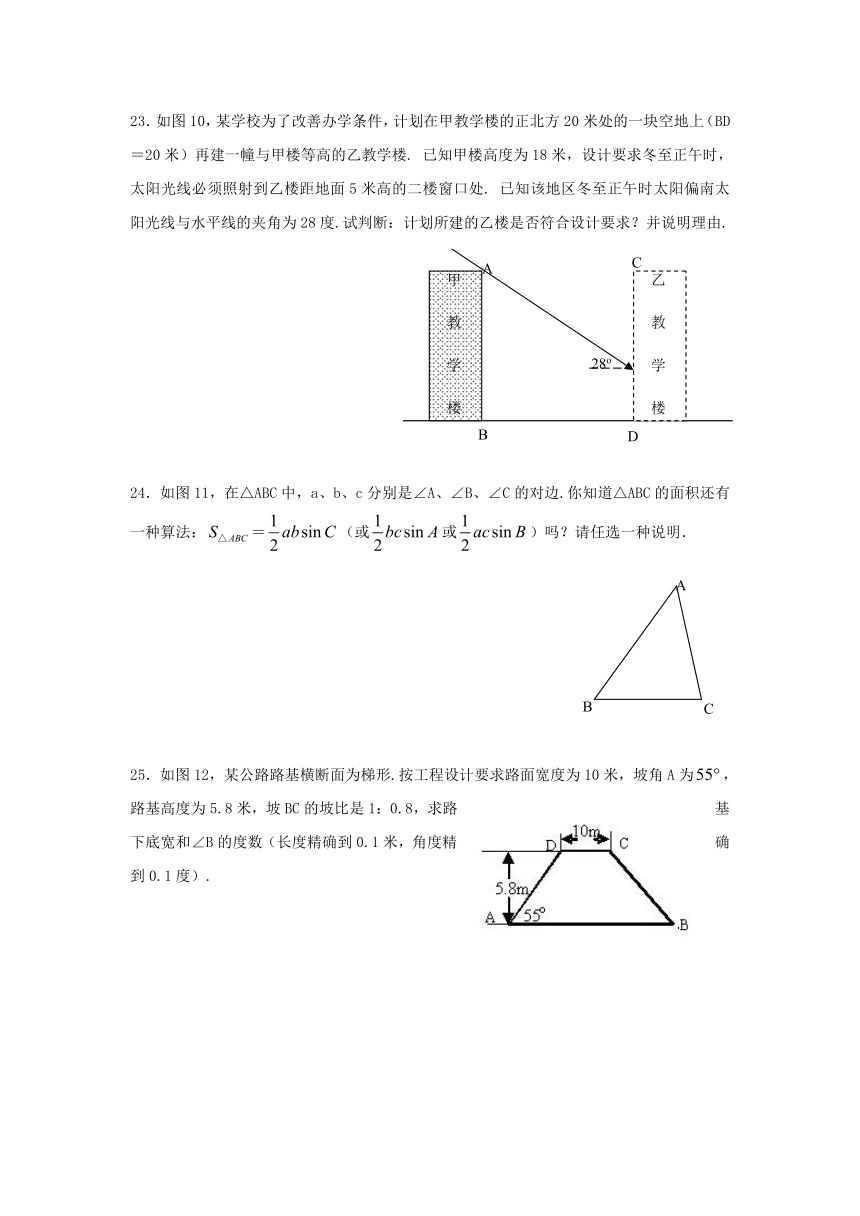
23.如图10,某学校为了改善办学条件,计划在甲教学楼的正北方20米处的一块空地上(BD=20米)再建一幢与甲楼等高的乙教学楼. 已知甲楼高度为18米,设计要求冬至正午时,太阳光线必须照射到乙楼距地面5米高的二楼窗口处. 已知该地区冬至正午时太阳偏南太阳光线与水平线的夹角为28度.试判断:计划所建的乙楼是否符合设计要求?并说明理由.
24.如图11,在△ABC中,a、b、c分别是∠A、∠B、∠C的对边.你知道△ABC的面积还有一种算法:=(或或)吗?请任选一种说明.
25.如图12,某公路路基横断面为梯形.按工程设计要求路面宽度为10米,坡角A为,路基高度为5.8米,坡BC的坡比是1:0.8,求路基下底宽和∠B的度数(长度精确到0.1米,角度精确到0.1度).
26.如图13,在一个坡角为15°的斜坡上,有一根垂直于水平面的旗杆,从点C测得对旗杆顶A的视线与斜坡面的夹角为50°,C到旗杆底部B的距离为2.5米,求旗杆AB的高.
(精确到0.01米)
综合提高
27. 如图14,挂着广告标语的氢气球升在广场上空,已知气球的直径为4m,在地面A点测得气球中心O的仰角为∠OAD=60°,测得气球的视角∠BAC=2°(AB、AC为⊙O的切线,B、C为切点).求气球中心O离地面的高度OD.(精确到1m )
28.为了测量某段河面的宽度,小亮同学设计了如图15所示的测量方案:
① 先在河的北岸选一定点A,
② 再在河的南岸选定相距a米的两点B、C,
③ 分别测得∠ABC=α,∠ACB=β;
请你根据小亮同学测得的数据,计算出河宽AD.(结果用含a和含α、β的三角函数表示)
解直角三角形参考答案
一、填空题:
1. 2. 3.36.9 4.4 5.0.2554、0.9730 6.5.0
7. 8.,80.4 9.38.5 10.9、12、15 11.19°2’
12.
二、选择题:
13.A 14.A 15.B 16.C 17.D 18.C 19.B 20.D
三、解答题
21.(1)=16,,∠A=30° (2)10,∠A =∠B= 45°
22.在Rt△AOB中,∵,∴∠AOB,
∵∠AOB=28°,∴=46.95.46.95÷2=23.475≈23.48.
这艘船航行的速度是23.48海里/小时.
23.方法一:如图,在△ACE中,∠ACE=90°,
∵∠CAE=,∴∠CAE ≈35.8°,
∵35.8°>28°,∴乙楼符合设计要求.
方法二:冬至正午时甲楼落在乙楼的影子高度
为20-2028°=20-20×0.5317≈9.4(米),
9.4>5,∴乙楼符合设计要求.
24.如图,过A点作AD⊥BC,垂足为D,
∵在△ABD中,∠ADB=90°,
∴,即AD=,
∵=,∴=.
25.如图,分别过点D、C作DE⊥AB,CF⊥AB,
垂足分别是E、F,
在△ADE中,∠DEA=90°,∠DAE=55°,
∴=55°,AE==≈4.06,
∵在△BFC中,∠BFC=90°,CF=5.8
∴=1:0.8,∴∠B≈51.3°,BF=5.8×0.8=4.64,
∵四边形DEFC是矩形,∴EF=CD,∴AB=4.06+10+4.64=18.7(米)
答:路基下底宽约是18.7米,∠B约是51.3°.
26.如图,过C点作CD⊥AB,交AB延长线于点D,
∵CD平行于水平面,∴∠BCD=15°,
在△BCD中,∠BDC=90°,∠BCD=15°,CB=2.5,
∵∠BCD,∴BD==2.5×0.2588=0.647,
∵∠BCD,∴CD==2.5×0.9659≈2.415,
在△ACD中,∠ADC=90°,
∵∠ACD,∠ACD=∠ACB+∠BCD=65°,CD=2.415
∴AD===2.415×2.145≈5.180,
∴AB=AD-BD=5.180-0.647≈4.53(米),
答:旗杆AB的高约为4.53米.
综合提高
27.连结OC,
∵AB、AC切⊙O于B、C,O是圆心,∴AO平分∠BAC,∴∠OAC=∠BAC=1°,
∵在Rt△OAC中,∠OAC ,∴=228.57()
∵在Rt△OAD中,∠OAD,∴=228.57×≈198()
答:气球中心O离地面的高度OD约是198.
28.因为tanα= ,所以BD=,同理,CD= ,所以+=,所以AD=(米).
B
A
O
北
东
西
南
62°
甲教学楼
乙教学楼
28o
A
B
D
C
A
B
C
B
D
A
C
O
一、填空题:
1.在△ABC中,C=90°,若=1,sinA=,则= .
2.旗杆的上一段BC被风吹断(C处仍连接),顶端着地与地面成30°角,顶端着地处B与旗杆底端相距4米,则旗杆原来高度为_________米. (结果保留根号)
3.已知直角三角形的两直角边的比为3:4,则最小角度数为_______°.(精确到0.1度)
4.已知△ABC的周长为4+2,则BC= .
5.利用计算器求值(保留4位有效数字):cos75°12′= ; 44°13′= .
6.伽利略曾用“比萨斜塔”进行重力定律实验.他从55米长的塔顶让一重物自由下落,物体的着地点离塔底4.8米,斜塔偏离铅垂线的角度是 °(精确到0.1度)
7.一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A测得某灯塔位于它的北偏东30°的B处(如图1).上午九时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里.(结果保留根号)
8.若一个等腰三角形的两边长分别为2cm和6cm,则底边上的高为__________cm,底角的度数是__________(精确到0.1度).
9.小强和小明去测量一座古塔的高度(如图2),他们在离古塔60米的A处,用测角仪测得古塔塔顶的仰角为32°,已知测角仪器高AD=1米,则古塔BE的高度为_______米.(精确到0.1米)
10.在Rt△ABC中,∠C=90°,,,则a=__________,b=__________,=__________.
11.如图,一护栏AB被一钢缆CD固定,CD与地面成25°36’的角,且DB=5,现再在C点上方2处加固另一钢缆ED,那么∠EDC=___________.(精确到分)
12.如图4,从楼顶A点测得电视塔CD的仰角为α,俯角为β,若楼房与电视塔之间的水平距离为m,则电视塔的高度CD是__________.
第7题 第9题 第11题 第12题
二、选择题:
13.在Rt△ABC中,∠C=90°,cosA=,=,则等于( ).
A.1 B. C.2 D.3
14.已知A=1.7321,锐角A=( ).
A. 60° B.58° C.40° D. 10°
15.甲、乙、丙三人放风筝,各人放出的风筝线长分别为60m、50m、40m,线与地平面所成的角分别为30o、45o、60o,假设风筝线近似看作是拉直的,则所放风筝最高的是( ).
A.甲 B.乙 C.丙 D.不能确定
16.如图5,为了测量河两岸的A、B两点间的距离,在与AB垂直的方向上取点C,测得AC=a,∠ACB=α,则AB的长为 ( ).
A. B. C. D.
17.如图6,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为( ).
A. 1 B. C. D.
18.在Rt△ABC中,∠B=90°,∠ACB=45°,点D在BC的延长线上,且CD=CA,则和tan22°30′的值相等的是( ).
A. B. C. D.
19.如图7,水库大坝的横断面是梯形,坝顶宽6,坝高24,斜坡的坡角为,斜坡的坡角D的正切值为,则坡底AD的长为( ).
A. B.42 C. D.
20.如图8所示,一勘测人员从B出发,沿坡度为15°的坡面以2.5千米/时的速度行至D点,用了24分钟,然后沿坡度为20°的坡面以1.5千米/时行至山顶A处,用了20分钟,则山高AC的长度是( ).
A. B.
C. D.
第16题 第17题 第19题 第20题
三、解答题
21.△ABC中,∠C=90°,根据下列条件,解直角三角形:
(1)=8,∠B=60° (2)=10,=10
22.如图9,灯塔A在港口O的北偏东62°方向上,且与港口的距离为100海里,一艘船上午9时从港口O出发向正东方向航行,上午11时到达B处,看到灯塔A在它的正北方向.试求这艘船航行的速度(精确到0.01海里/小时).
23.如图10,某学校为了改善办学条件,计划在甲教学楼的正北方20米处的一块空地上(BD=20米)再建一幢与甲楼等高的乙教学楼. 已知甲楼高度为18米,设计要求冬至正午时,太阳光线必须照射到乙楼距地面5米高的二楼窗口处. 已知该地区冬至正午时太阳偏南太阳光线与水平线的夹角为28度.试判断:计划所建的乙楼是否符合设计要求?并说明理由.
24.如图11,在△ABC中,a、b、c分别是∠A、∠B、∠C的对边.你知道△ABC的面积还有一种算法:=(或或)吗?请任选一种说明.
25.如图12,某公路路基横断面为梯形.按工程设计要求路面宽度为10米,坡角A为,路基高度为5.8米,坡BC的坡比是1:0.8,求路基下底宽和∠B的度数(长度精确到0.1米,角度精确到0.1度).
26.如图13,在一个坡角为15°的斜坡上,有一根垂直于水平面的旗杆,从点C测得对旗杆顶A的视线与斜坡面的夹角为50°,C到旗杆底部B的距离为2.5米,求旗杆AB的高.
(精确到0.01米)
综合提高
27. 如图14,挂着广告标语的氢气球升在广场上空,已知气球的直径为4m,在地面A点测得气球中心O的仰角为∠OAD=60°,测得气球的视角∠BAC=2°(AB、AC为⊙O的切线,B、C为切点).求气球中心O离地面的高度OD.(精确到1m )
28.为了测量某段河面的宽度,小亮同学设计了如图15所示的测量方案:
① 先在河的北岸选一定点A,
② 再在河的南岸选定相距a米的两点B、C,
③ 分别测得∠ABC=α,∠ACB=β;
请你根据小亮同学测得的数据,计算出河宽AD.(结果用含a和含α、β的三角函数表示)
解直角三角形参考答案
一、填空题:
1. 2. 3.36.9 4.4 5.0.2554、0.9730 6.5.0
7. 8.,80.4 9.38.5 10.9、12、15 11.19°2’
12.
二、选择题:
13.A 14.A 15.B 16.C 17.D 18.C 19.B 20.D
三、解答题
21.(1)=16,,∠A=30° (2)10,∠A =∠B= 45°
22.在Rt△AOB中,∵,∴∠AOB,
∵∠AOB=28°,∴=46.95.46.95÷2=23.475≈23.48.
这艘船航行的速度是23.48海里/小时.
23.方法一:如图,在△ACE中,∠ACE=90°,
∵∠CAE=,∴∠CAE ≈35.8°,
∵35.8°>28°,∴乙楼符合设计要求.
方法二:冬至正午时甲楼落在乙楼的影子高度
为20-2028°=20-20×0.5317≈9.4(米),
9.4>5,∴乙楼符合设计要求.
24.如图,过A点作AD⊥BC,垂足为D,
∵在△ABD中,∠ADB=90°,
∴,即AD=,
∵=,∴=.
25.如图,分别过点D、C作DE⊥AB,CF⊥AB,
垂足分别是E、F,
在△ADE中,∠DEA=90°,∠DAE=55°,
∴=55°,AE==≈4.06,
∵在△BFC中,∠BFC=90°,CF=5.8
∴=1:0.8,∴∠B≈51.3°,BF=5.8×0.8=4.64,
∵四边形DEFC是矩形,∴EF=CD,∴AB=4.06+10+4.64=18.7(米)
答:路基下底宽约是18.7米,∠B约是51.3°.
26.如图,过C点作CD⊥AB,交AB延长线于点D,
∵CD平行于水平面,∴∠BCD=15°,
在△BCD中,∠BDC=90°,∠BCD=15°,CB=2.5,
∵∠BCD,∴BD==2.5×0.2588=0.647,
∵∠BCD,∴CD==2.5×0.9659≈2.415,
在△ACD中,∠ADC=90°,
∵∠ACD,∠ACD=∠ACB+∠BCD=65°,CD=2.415
∴AD===2.415×2.145≈5.180,
∴AB=AD-BD=5.180-0.647≈4.53(米),
答:旗杆AB的高约为4.53米.
综合提高
27.连结OC,
∵AB、AC切⊙O于B、C,O是圆心,∴AO平分∠BAC,∴∠OAC=∠BAC=1°,
∵在Rt△OAC中,∠OAC ,∴=228.57()
∵在Rt△OAD中,∠OAD,∴=228.57×≈198()
答:气球中心O离地面的高度OD约是198.
28.因为tanα= ,所以BD=,同理,CD= ,所以+=,所以AD=(米).
B
A
O
北
东
西
南
62°
甲教学楼
乙教学楼
28o
A
B
D
C
A
B
C
B
D
A
C
O
