数学人教A版(2019)必修第二册6.4.1平面几何中的向量方法 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.4.1平面几何中的向量方法 课件(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 330.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-18 20:24:01 | ||
图片预览




文档简介
(共15张PPT)
6.4.1 平面几何中的向量方法
复习提问
(1)向量共线的等价条件:
与 共线
(2)平面向量基本定理
(3)平面向量的数量积
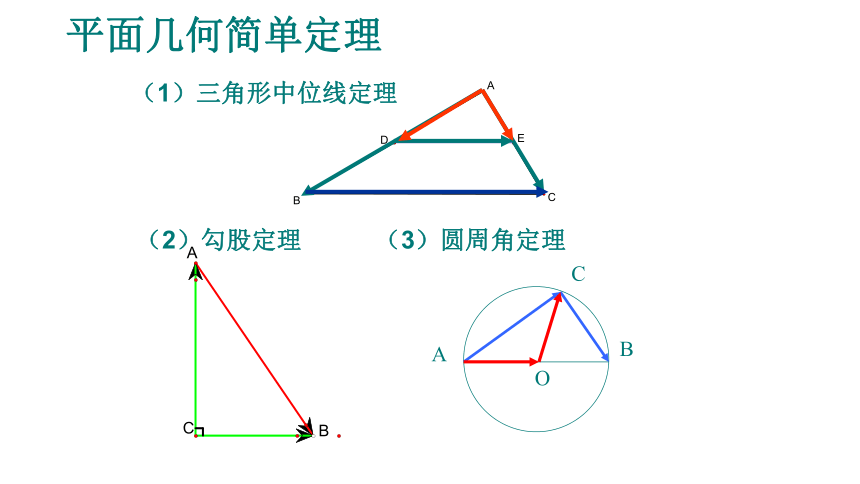
平面几何简单定理
(1)三角形中位线定理
(2)勾股定理
(3)圆周角定理
A
B
C
O
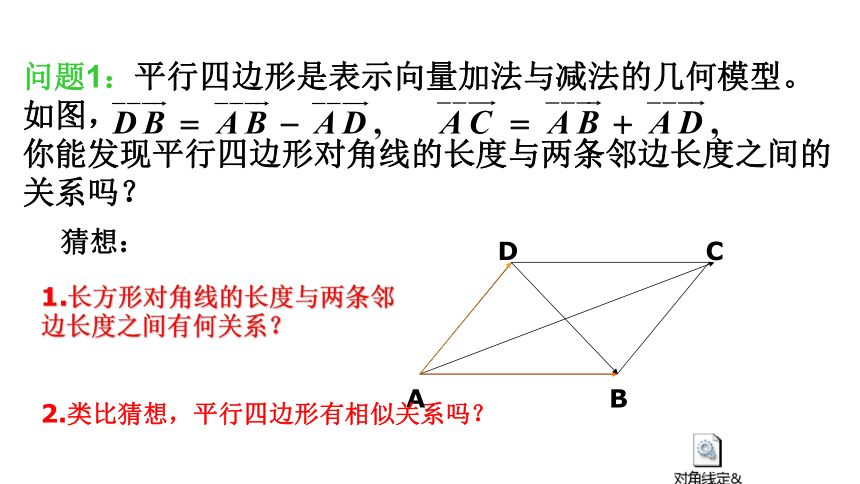
问题1:平行四边形是表示向量加法与减法的几何模型。如图,
你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?
A
B
C
D
猜想:
1.长方形对角线的长度与两条邻边长度之间有何关系?
2.类比猜想,平行四边形有相似关系吗?
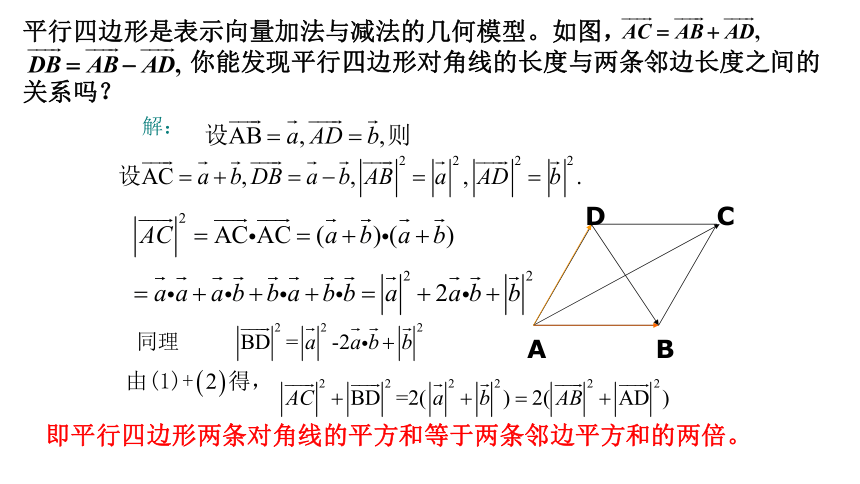
平行四边形是表示向量加法与减法的几何模型。如图,
你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?
A
B
C
D
解:
即平行四边形两条对角线的平方和等于两条邻边平方和的两倍。
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
一 用向量方法解决平面几何问题的“三步曲”:
简述:形到向量 向量的运算 向量和数到形
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。
二、利用向量证明平面几何的两种经典方法及步骤:1、线性运算法(1)选取合适的基底(一般选择夹角和模长已知的两个向量);(2)利用基底表示相关向量;(3)利用向量的线性运算或数量积找到相应关系;(4)把计算结果“翻译”为几何问题。2、坐标运算法(1)建立适当的直角坐标系(尽可能让更多的点在坐标系上);(2)把相关向量坐标化;(3)用向量的坐标运算找到相应关系;(4)利用向量关系回答几何问题。
题型一 利用向量证明线段垂直
题型二 利用向量证明线段平行
D
题型三 利用向量求线段长度
探究1、已知:如图AD、BE、CF是△ABC三条高,求证:AD、BE、CF交于一点
F
A
B
C
D
E
A
B
C
D
E
H
分析:
思路一:设AD与BE交于H,只要证
CH⊥AB,即高CF与CH重合,即CF
过点H
由此可设
利用AD⊥BC,BE⊥CA,对应向量垂直。
探究与思考
课堂小结
用向量方法解决平面几何问题的“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题
中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。
平面几何中证明问题的具体转化方法
因为有了运算,向量的力量无限,如果不能进行运算,向量只是示意方向的路标。
课后作业
1、6.4.1册子
2、预习,思考下列问题
(1)怎么样把物理问题转化为数学问题?
(2)如何用数学模型解释相应的物理现象?
6.4.1 平面几何中的向量方法
复习提问
(1)向量共线的等价条件:
与 共线
(2)平面向量基本定理
(3)平面向量的数量积
平面几何简单定理
(1)三角形中位线定理
(2)勾股定理
(3)圆周角定理
A
B
C
O
问题1:平行四边形是表示向量加法与减法的几何模型。如图,
你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?
A
B
C
D
猜想:
1.长方形对角线的长度与两条邻边长度之间有何关系?
2.类比猜想,平行四边形有相似关系吗?
平行四边形是表示向量加法与减法的几何模型。如图,
你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?
A
B
C
D
解:
即平行四边形两条对角线的平方和等于两条邻边平方和的两倍。
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
一 用向量方法解决平面几何问题的“三步曲”:
简述:形到向量 向量的运算 向量和数到形
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。
二、利用向量证明平面几何的两种经典方法及步骤:1、线性运算法(1)选取合适的基底(一般选择夹角和模长已知的两个向量);(2)利用基底表示相关向量;(3)利用向量的线性运算或数量积找到相应关系;(4)把计算结果“翻译”为几何问题。2、坐标运算法(1)建立适当的直角坐标系(尽可能让更多的点在坐标系上);(2)把相关向量坐标化;(3)用向量的坐标运算找到相应关系;(4)利用向量关系回答几何问题。
题型一 利用向量证明线段垂直
题型二 利用向量证明线段平行
D
题型三 利用向量求线段长度
探究1、已知:如图AD、BE、CF是△ABC三条高,求证:AD、BE、CF交于一点
F
A
B
C
D
E
A
B
C
D
E
H
分析:
思路一:设AD与BE交于H,只要证
CH⊥AB,即高CF与CH重合,即CF
过点H
由此可设
利用AD⊥BC,BE⊥CA,对应向量垂直。
探究与思考
课堂小结
用向量方法解决平面几何问题的“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题
中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。
平面几何中证明问题的具体转化方法
因为有了运算,向量的力量无限,如果不能进行运算,向量只是示意方向的路标。
课后作业
1、6.4.1册子
2、预习,思考下列问题
(1)怎么样把物理问题转化为数学问题?
(2)如何用数学模型解释相应的物理现象?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
