6.1平面向量的概念 同步练习(含答案)
文档属性
| 名称 | 6.1平面向量的概念 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 06:19:38 | ||
图片预览

文档简介
6.1 平面向量的概念
(同步练习)
一、单选题
1.如图,在四边形ABCD中,若,则图中相等的向量是( )
A.与 B.与 C.与 D.与
2.给出下列说法:①零向量是没有方向的;②零向量的长度为0;③零向量的方向是任意的;④单位向量的模都相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.设是非零向量,分别是的单位向量,则下列各式中正确的是( )
A. B.或
C. D.
4.下列说法正确的是( )
①有向线段三要素是始点、方向、长度;
②向量两要素是大小和方向;
③同向且等长的有向线段表示同一向量;
④在平行四边形中,.
A.① B.①② C.①②③ D.①②③④
5.下列命题中正确的是( )
A.单位向量都相等 B.相等向量一定是共线向量
C.若,则 D.任意向量的模都是正数
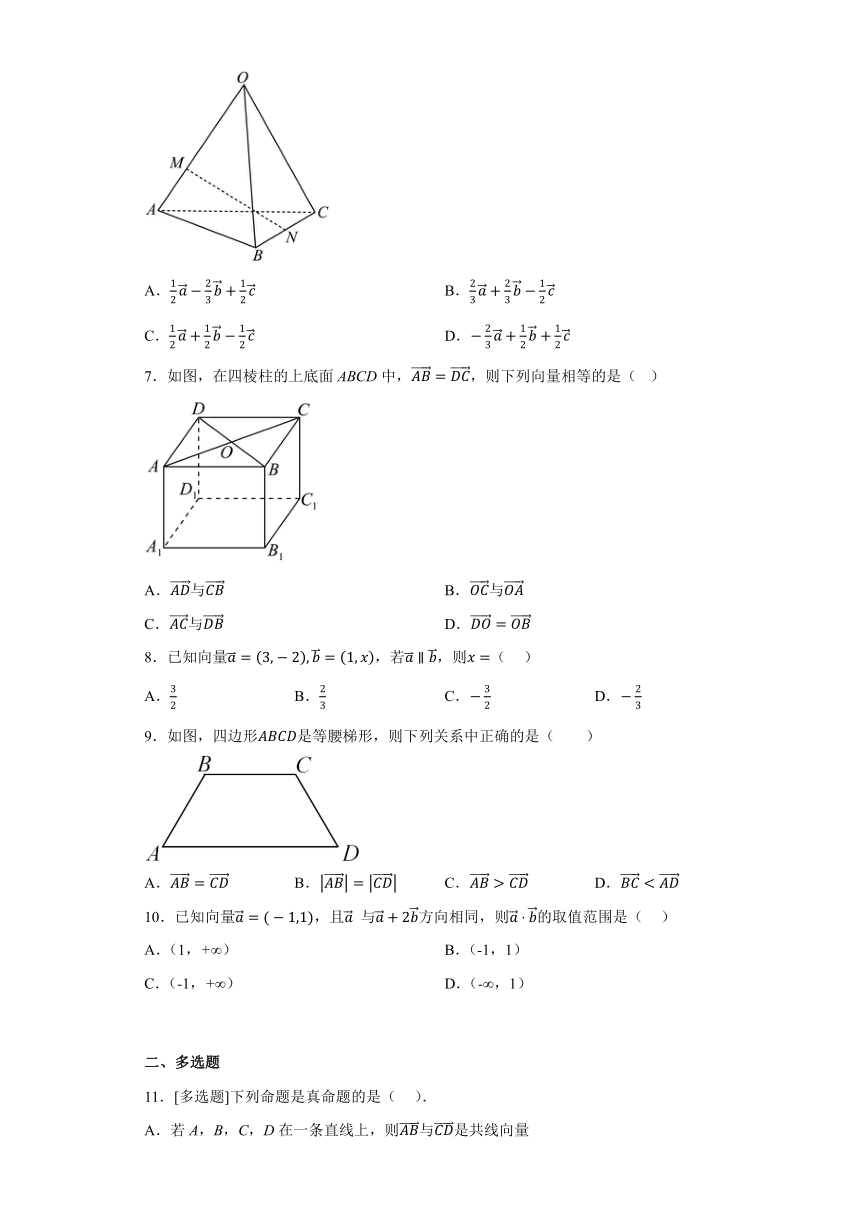
6.如图.空间四边形OABC中,,点M在OA上,且满足,点N为BC的中点,则( )
A. B.
C. D.
7.如图,在四棱柱的上底面ABCD中,,则下列向量相等的是( )
A.与 B.与
C.与 D.
8.已知向量,若,则( )
A. B. C. D.
9.如图,四边形是等腰梯形,则下列关系中正确的是( )
A. B. C. D.
10.已知向量,且 与方向相同,则的取值范围是( )
A.(1,+∞) B.(-1,1)
C.(-1,+∞) D.(-∞,1)
二、多选题
11.[多选题]下列命题是真命题的是( ).
A.若A,B,C,D在一条直线上,则与是共线向量
B.若A,B,C,D不在一条直线上,则与不是共线向量
C.若向量与是共线向量,则A,B,C,D四点必在一条直线上
D.若向量与是共线向量,则A,B,C三点必在一条直线上
12.下列说法中正确的是( )
A.若为单位向量,则 B.若与共线,则或
C.若,则 D.是与非零向量共线的单位向量
13.下列结论中正确的是( )
A.若,则
B.若,则
C.若A,B,C,D是不共线的四点,则“”是“四边形ABCD为平行四边形”的充要条件
D.“”的充要条件是“且”
14.下列结论中正确的是( )
A.与是否相等与,的方向无关 B.零向量相等,零向量的相反向量是零向量
C.若,都是单位向量,则 D.向量与相等
三、填空题
15.下列各量中,向量有:______.(填写序号)
①浓度;②年龄;③风力;④面积;⑤位移;⑥人造卫星的速度;⑦电量;⑧向心力;⑨盈利;⑩加速度.
16.已知点满足,若,,则点的坐标为______.
17.,,,均为非零向量,且,,,则四边形ABCD的形状是______.
18.如图,B是线段AC的中点,若分别以图中各点为起点和终点,则最多可以写出______个互不相等的非零向量.
19.已知向量,,且与共线,则实数______.
四、解答题
20.如图,多边形ABCDEF为正六边形,在以此六边形各顶点和中心为起点、终点的向量中:
(1)写出与相等的向量;
(2)写出的负向量;
(3)写出与平行的向量;
(4)写出与长度相等的向量.
21.在平面直角坐标系中,已知,与x轴的正方向所成的角为30°,与y轴的正方向所成的角为120°,试作出.
22.如图所示,在平行四边形中,,分别是,的中点.
(1)写出与向量共线的向量;
(2)求证:.
23.如图是4×3的矩形(每个小方格的边长都是1),在起点和终点都在小方格的顶点处的向量中,与向量平行且模为的向量共有几个?与向量方向相同且模为的向量共有几个?
24.已知向量.
(1)求证:三点共线.
(2)若,求的值.
25.已知向量.
(1)求与平行的单位向量;
(2)设,若存在,使得成立,求k的取值范围.
参考答案:
1.C2.C3.D4.D5.B6.D7.D8.D9.B10.C
11.AD
12.CD
13.BC
14.AB
15.③⑤⑥⑧⑩
16.
17.矩形
18.4
19.2
20.(1),,
(2),,,
(3),,,,,,,,
(4),,,,
21.(1)解:因为在平行四边形中,,分别是,的中点,,,
所以四边形为平行四边形,所以.
所以与向量共线的向量为:,,.
(2)证明:在平行四边形中,,.
因为,分别是,的中点,
所以且,
所以四边形是平行四边形,
所以,,
故.
23.24个;2个.
24.(1)证明:∵,故三点共线;
(2),,
则有,即,解得
25.(1)或
(2)
(同步练习)
一、单选题
1.如图,在四边形ABCD中,若,则图中相等的向量是( )
A.与 B.与 C.与 D.与
2.给出下列说法:①零向量是没有方向的;②零向量的长度为0;③零向量的方向是任意的;④单位向量的模都相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.设是非零向量,分别是的单位向量,则下列各式中正确的是( )
A. B.或
C. D.
4.下列说法正确的是( )
①有向线段三要素是始点、方向、长度;
②向量两要素是大小和方向;
③同向且等长的有向线段表示同一向量;
④在平行四边形中,.
A.① B.①② C.①②③ D.①②③④
5.下列命题中正确的是( )
A.单位向量都相等 B.相等向量一定是共线向量
C.若,则 D.任意向量的模都是正数
6.如图.空间四边形OABC中,,点M在OA上,且满足,点N为BC的中点,则( )
A. B.
C. D.
7.如图,在四棱柱的上底面ABCD中,,则下列向量相等的是( )
A.与 B.与
C.与 D.
8.已知向量,若,则( )
A. B. C. D.
9.如图,四边形是等腰梯形,则下列关系中正确的是( )
A. B. C. D.
10.已知向量,且 与方向相同,则的取值范围是( )
A.(1,+∞) B.(-1,1)
C.(-1,+∞) D.(-∞,1)
二、多选题
11.[多选题]下列命题是真命题的是( ).
A.若A,B,C,D在一条直线上,则与是共线向量
B.若A,B,C,D不在一条直线上,则与不是共线向量
C.若向量与是共线向量,则A,B,C,D四点必在一条直线上
D.若向量与是共线向量,则A,B,C三点必在一条直线上
12.下列说法中正确的是( )
A.若为单位向量,则 B.若与共线,则或
C.若,则 D.是与非零向量共线的单位向量
13.下列结论中正确的是( )
A.若,则
B.若,则
C.若A,B,C,D是不共线的四点,则“”是“四边形ABCD为平行四边形”的充要条件
D.“”的充要条件是“且”
14.下列结论中正确的是( )
A.与是否相等与,的方向无关 B.零向量相等,零向量的相反向量是零向量
C.若,都是单位向量,则 D.向量与相等
三、填空题
15.下列各量中,向量有:______.(填写序号)
①浓度;②年龄;③风力;④面积;⑤位移;⑥人造卫星的速度;⑦电量;⑧向心力;⑨盈利;⑩加速度.
16.已知点满足,若,,则点的坐标为______.
17.,,,均为非零向量,且,,,则四边形ABCD的形状是______.
18.如图,B是线段AC的中点,若分别以图中各点为起点和终点,则最多可以写出______个互不相等的非零向量.
19.已知向量,,且与共线,则实数______.
四、解答题
20.如图,多边形ABCDEF为正六边形,在以此六边形各顶点和中心为起点、终点的向量中:
(1)写出与相等的向量;
(2)写出的负向量;
(3)写出与平行的向量;
(4)写出与长度相等的向量.
21.在平面直角坐标系中,已知,与x轴的正方向所成的角为30°,与y轴的正方向所成的角为120°,试作出.
22.如图所示,在平行四边形中,,分别是,的中点.
(1)写出与向量共线的向量;
(2)求证:.
23.如图是4×3的矩形(每个小方格的边长都是1),在起点和终点都在小方格的顶点处的向量中,与向量平行且模为的向量共有几个?与向量方向相同且模为的向量共有几个?
24.已知向量.
(1)求证:三点共线.
(2)若,求的值.
25.已知向量.
(1)求与平行的单位向量;
(2)设,若存在,使得成立,求k的取值范围.
参考答案:
1.C2.C3.D4.D5.B6.D7.D8.D9.B10.C
11.AD
12.CD
13.BC
14.AB
15.③⑤⑥⑧⑩
16.
17.矩形
18.4
19.2
20.(1),,
(2),,,
(3),,,,,,,,
(4),,,,
21.(1)解:因为在平行四边形中,,分别是,的中点,,,
所以四边形为平行四边形,所以.
所以与向量共线的向量为:,,.
(2)证明:在平行四边形中,,.
因为,分别是,的中点,
所以且,
所以四边形是平行四边形,
所以,,
故.
23.24个;2个.
24.(1)证明:∵,故三点共线;
(2),,
则有,即,解得
25.(1)或
(2)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
