8.3.1 棱柱、棱锥、棱台的表面积和体积 同步练习-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案)
文档属性
| 名称 | 8.3.1 棱柱、棱锥、棱台的表面积和体积 同步练习-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 964.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 06:34:04 | ||
图片预览




文档简介
8.3.1 棱柱、棱锥、棱台的表面积和体积 同步练习
一、单选题
1.已知斜三棱柱的一个侧面的面积为10,该侧面与其相对侧棱的距离为3,则此斜三棱柱的体积为( )
A.30 B.15 C.10 D.60
2.一件刚出土的珍费文物要在博物馆大厅中央展出,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积为0.5立方米,其底部是直径为0.9米的圆(如图),要求文物底部与玻璃罩底边间隔0.3米,文物顶部与玻璃罩上底面间隔0.2米,气体每立方米1000元,则气体费用为( )
A.4500元 B.4000元 C.2880元 D.2380元
3.过棱长为2的正方体的三个顶点作一截面,此截面恰好切去一个三棱锥,则该正方体剩余几何体的体积为( )
A.4 B.6 C. D.
4.已知用斜二测画法画梯形OABC的直观图如图所示,,,,轴,,为的三等分点,则四边形OABC绕y轴旋转一周形成的空间几何体的体积为( )
A. B. C. D.
5.已知四棱台的上、下底面分别是边长为和的正方形,侧面均为腰长为的等腰梯形,则该四棱台的表面积为( )
A. B.
C. D.
6.如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )
A.258 B.234 C.222 D.210
7.在棱长为1的正方体的表面上任取4个点构成一个三棱锥,则这个三棱锥体积的取值范围是( )
A. B. C. D.
8.若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的表面积为( )
A. B. C. D.
二、多选题
9.有一个三棱锥,其中一个面为边长为2的正三角形,有两个面为等腰直角三角形,则该几何体的体积可能是( )
A. B. C. D.
10.“堑堵”“阳马”和“鳖臑”是我国古代对一些特殊几何体的称谓.《九章算术·商功》有如下叙述:“斜解立方,得两堑堵,斜解堑堵.其一为阳马,其一为鳖臑”.意思是说:将一个长方体沿对角面斜截(图1),得到一模一样的两个堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜截(图2),得一个四棱锥称为阳马(图3),一个三棱锥称为鳖臑(图4).
若长方体的体积为V,由该长方体斜截所得到的堑堵、阳马和鳖臑的体积分别为,则下列选项不正确的是( )
A. B. C. D.
11.如图,直三棱柱中,,,,侧面中心为O,点E是侧棱上的一个动点,有下列判断,正确的是( )
A.直三棱柱侧面积是 B.直三棱柱体积是
C.三棱锥的体积为定值 D.的最小值为
12.如图,已知四棱锥中,底面,分别是的中点,且,记三棱锥的体积分别为,则( )
A. B.
C. D.
三、填空题
13.已知平行六面体各棱长均为,在由顶点出发的三条棱上,取,,,则棱锥的体积是该平行六面体体积的______.
14.某正三棱台的各顶点之间的距离构成的集合为,则该棱台的体积为______.
15.如图,直四棱柱中,底面,四边形为梯形,,且,过,,三点的平面记为,与平面的交点为.则此四棱柱被平面分成上、下两部分的体积之比为__.
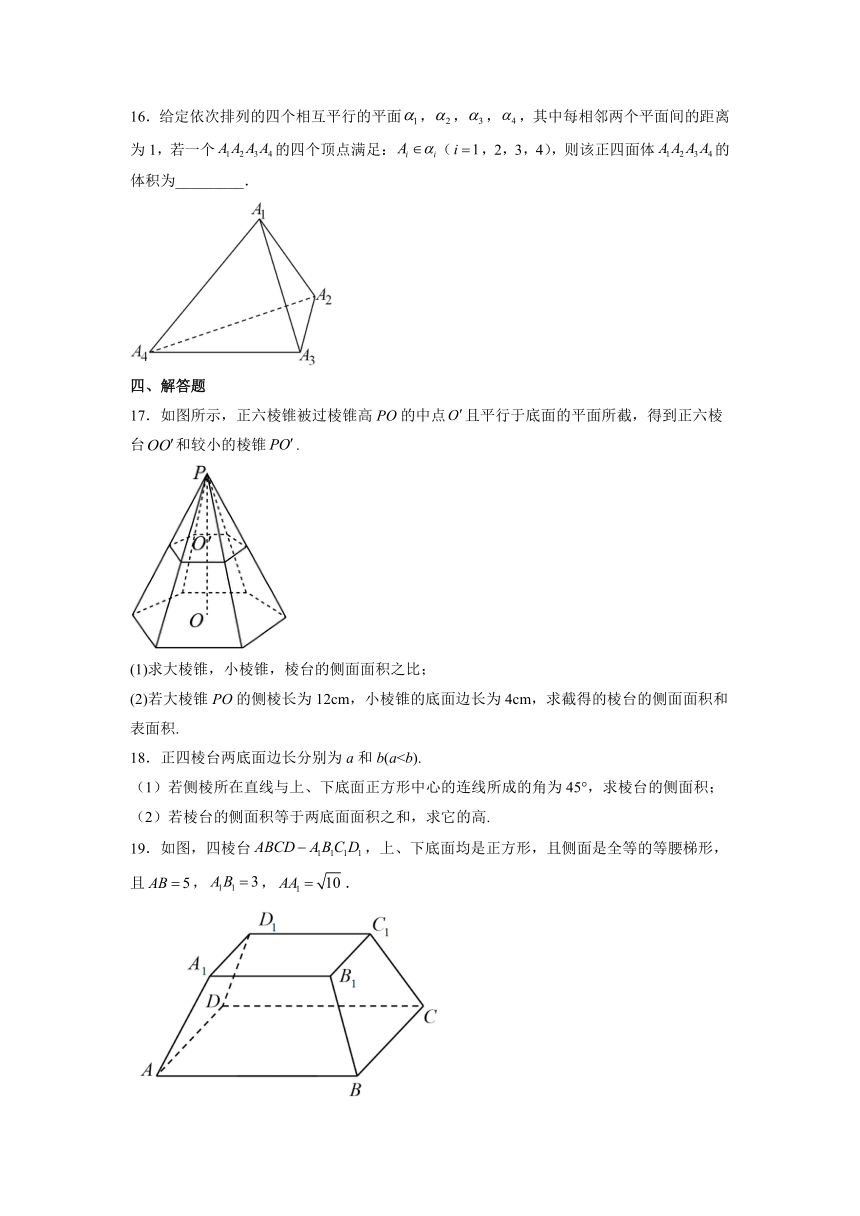
16.给定依次排列的四个相互平行的平面,,,,其中每相邻两个平面间的距离为1,若一个的四个顶点满足:(,2,3,4),则该正四面体的体积为_________.
四、解答题
17.如图所示,正六棱锥被过棱锥高PO的中点且平行于底面的平面所截,得到正六棱台和较小的棱锥.
(1)求大棱锥,小棱锥,棱台的侧面面积之比;
(2)若大棱锥PO的侧棱长为12cm,小棱锥的底面边长为4cm,求截得的棱台的侧面面积和表面积.
18.正四棱台两底面边长分别为a和b(a(1)若侧棱所在直线与上、下底面正方形中心的连线所成的角为45°,求棱台的侧面积;
(2)若棱台的侧面积等于两底面面积之和,求它的高.
19.如图,四棱台,上、下底面均是正方形,且侧面是全等的等腰梯形,且,,.
(1)求四棱台的侧面积;
(2)求四棱台的体积.
20.正三棱柱侧面展开图是边长为2和4的矩形,求它的表面积.
21.棱锥是生活中最常见的空间图形之一,譬如我们熟悉的埃及金字塔,它的形状可视为一个正四棱锥.我国数学家很早就开始研究棱锥问题,公元一世纪左右成书的《九章算术》第五章中的第十二题,计算了正方锥、直方锥(阳马)、直三角锥(鳖臑)的体积,并给出了通用公式.公元三世纪中叶,数学家刘徽在给《九章算术》作的注中,运用极限思想证明了棱锥的体积公式.请你使用学过的相关知识,解决下列问题:如图,正三棱锥中,三条侧棱SA,SB,SC两两垂直,侧棱长是3,底面内一点P到侧面的距离分别为x,y,z.
(1)求证:;
(2)若,试确定点P在底面内的位置.
22.正四棱台的下底边长,它的内切球半径为3.
(1)求正四棱台的表面积;
(2)求与底面所成角的正弦值.
参考答案
1--8BBCBC CBB
9.BCD 10.ACD 11.ACD 12.ACD
13.
14.
15.
16.
17.(1)设小棱锥的底面边长为,斜高为,则大棱锥的底面边长为,斜高为,
所以大棱锥的侧面积为,小棱锥的侧面积为,
棱台的侧面积为,
所以大棱锥,小棱锥,棱台的侧面积之比.
(2)因为小棱锥的底面边长为4cm,所以大棱锥的底面边长为8cm,
因为大棱锥的侧棱长为12cm,所以大棱锥的斜高为cm,
所以大棱锥的侧面积为,
所以棱台的侧面积为,
棱台的上,下底面的面积和为,
所以棱台的表面积为.
18.解:(1)如图所示:
平面,侧棱所在直线与上、下底面正方形中心的连线所成的角为,
,,.
分别取,的中点,,连接,.
则,.
斜高.
棱台的侧面积;
(2)棱台的侧面积等于两底面面积之和,
,
.
.
19.(1)设棱台是由棱锥截出的,如图,
棱台的侧面是全等的等腰梯形,则棱锥的侧面是全等的等腰三角形,显然侧棱都相等,
设是底面上与的交点,则是的中点也是中点,
所以,,则平面,正方形中心,因此是正棱锥,棱台是正棱台,
在侧面内过作于点,
则,
棱台的侧面积为侧=;
(2)设是的中心,显然,
是直角梯形,,,
高,
棱台的体积为.
20.因为正三棱柱的侧面展开图是边长分别为2和4的矩形,
所以有以下两种情况:
当2是下底面的周长,4是正三棱柱的高时,
正三棱柱的表面积为;
当4是下底面的周长,2是正三棱柱的高时,
正三棱柱的表面积为;
故答案为:或.
21.(1)在正三棱锥中,SA,SB,SC两两垂直且AB=BC=CA,P为底面ABC内的一点,连接PA,PB,PC,PS,如图,可将原三棱锥分成三个三棱锥,
它们的高分别为,由,
即,
得
(2)由,得.
又,∴,∴,
当且仅当时取等号.
故当时,点P为正三角形的中心.
22.
(1)如图,做该正棱台的轴截面, 中, ,
所以 ,根据对称性, ,
故 所以 ,
正四棱台上底面是一个边长为 的正方形,
即
(2)正四棱台中,上下底面均为正方形,且侧棱长相等, 在底面的射影为 ,
所以 , 与底面所成角为 ,
,
, , .
一、单选题
1.已知斜三棱柱的一个侧面的面积为10,该侧面与其相对侧棱的距离为3,则此斜三棱柱的体积为( )
A.30 B.15 C.10 D.60
2.一件刚出土的珍费文物要在博物馆大厅中央展出,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积为0.5立方米,其底部是直径为0.9米的圆(如图),要求文物底部与玻璃罩底边间隔0.3米,文物顶部与玻璃罩上底面间隔0.2米,气体每立方米1000元,则气体费用为( )
A.4500元 B.4000元 C.2880元 D.2380元
3.过棱长为2的正方体的三个顶点作一截面,此截面恰好切去一个三棱锥,则该正方体剩余几何体的体积为( )
A.4 B.6 C. D.
4.已知用斜二测画法画梯形OABC的直观图如图所示,,,,轴,,为的三等分点,则四边形OABC绕y轴旋转一周形成的空间几何体的体积为( )
A. B. C. D.
5.已知四棱台的上、下底面分别是边长为和的正方形,侧面均为腰长为的等腰梯形,则该四棱台的表面积为( )
A. B.
C. D.
6.如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )
A.258 B.234 C.222 D.210
7.在棱长为1的正方体的表面上任取4个点构成一个三棱锥,则这个三棱锥体积的取值范围是( )
A. B. C. D.
8.若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的表面积为( )
A. B. C. D.
二、多选题
9.有一个三棱锥,其中一个面为边长为2的正三角形,有两个面为等腰直角三角形,则该几何体的体积可能是( )
A. B. C. D.
10.“堑堵”“阳马”和“鳖臑”是我国古代对一些特殊几何体的称谓.《九章算术·商功》有如下叙述:“斜解立方,得两堑堵,斜解堑堵.其一为阳马,其一为鳖臑”.意思是说:将一个长方体沿对角面斜截(图1),得到一模一样的两个堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜截(图2),得一个四棱锥称为阳马(图3),一个三棱锥称为鳖臑(图4).
若长方体的体积为V,由该长方体斜截所得到的堑堵、阳马和鳖臑的体积分别为,则下列选项不正确的是( )
A. B. C. D.
11.如图,直三棱柱中,,,,侧面中心为O,点E是侧棱上的一个动点,有下列判断,正确的是( )
A.直三棱柱侧面积是 B.直三棱柱体积是
C.三棱锥的体积为定值 D.的最小值为
12.如图,已知四棱锥中,底面,分别是的中点,且,记三棱锥的体积分别为,则( )
A. B.
C. D.
三、填空题
13.已知平行六面体各棱长均为,在由顶点出发的三条棱上,取,,,则棱锥的体积是该平行六面体体积的______.
14.某正三棱台的各顶点之间的距离构成的集合为,则该棱台的体积为______.
15.如图,直四棱柱中,底面,四边形为梯形,,且,过,,三点的平面记为,与平面的交点为.则此四棱柱被平面分成上、下两部分的体积之比为__.
16.给定依次排列的四个相互平行的平面,,,,其中每相邻两个平面间的距离为1,若一个的四个顶点满足:(,2,3,4),则该正四面体的体积为_________.
四、解答题
17.如图所示,正六棱锥被过棱锥高PO的中点且平行于底面的平面所截,得到正六棱台和较小的棱锥.
(1)求大棱锥,小棱锥,棱台的侧面面积之比;
(2)若大棱锥PO的侧棱长为12cm,小棱锥的底面边长为4cm,求截得的棱台的侧面面积和表面积.
18.正四棱台两底面边长分别为a和b(a
(2)若棱台的侧面积等于两底面面积之和,求它的高.
19.如图,四棱台,上、下底面均是正方形,且侧面是全等的等腰梯形,且,,.
(1)求四棱台的侧面积;
(2)求四棱台的体积.
20.正三棱柱侧面展开图是边长为2和4的矩形,求它的表面积.
21.棱锥是生活中最常见的空间图形之一,譬如我们熟悉的埃及金字塔,它的形状可视为一个正四棱锥.我国数学家很早就开始研究棱锥问题,公元一世纪左右成书的《九章算术》第五章中的第十二题,计算了正方锥、直方锥(阳马)、直三角锥(鳖臑)的体积,并给出了通用公式.公元三世纪中叶,数学家刘徽在给《九章算术》作的注中,运用极限思想证明了棱锥的体积公式.请你使用学过的相关知识,解决下列问题:如图,正三棱锥中,三条侧棱SA,SB,SC两两垂直,侧棱长是3,底面内一点P到侧面的距离分别为x,y,z.
(1)求证:;
(2)若,试确定点P在底面内的位置.
22.正四棱台的下底边长,它的内切球半径为3.
(1)求正四棱台的表面积;
(2)求与底面所成角的正弦值.
参考答案
1--8BBCBC CBB
9.BCD 10.ACD 11.ACD 12.ACD
13.
14.
15.
16.
17.(1)设小棱锥的底面边长为,斜高为,则大棱锥的底面边长为,斜高为,
所以大棱锥的侧面积为,小棱锥的侧面积为,
棱台的侧面积为,
所以大棱锥,小棱锥,棱台的侧面积之比.
(2)因为小棱锥的底面边长为4cm,所以大棱锥的底面边长为8cm,
因为大棱锥的侧棱长为12cm,所以大棱锥的斜高为cm,
所以大棱锥的侧面积为,
所以棱台的侧面积为,
棱台的上,下底面的面积和为,
所以棱台的表面积为.
18.解:(1)如图所示:
平面,侧棱所在直线与上、下底面正方形中心的连线所成的角为,
,,.
分别取,的中点,,连接,.
则,.
斜高.
棱台的侧面积;
(2)棱台的侧面积等于两底面面积之和,
,
.
.
19.(1)设棱台是由棱锥截出的,如图,
棱台的侧面是全等的等腰梯形,则棱锥的侧面是全等的等腰三角形,显然侧棱都相等,
设是底面上与的交点,则是的中点也是中点,
所以,,则平面,正方形中心,因此是正棱锥,棱台是正棱台,
在侧面内过作于点,
则,
棱台的侧面积为侧=;
(2)设是的中心,显然,
是直角梯形,,,
高,
棱台的体积为.
20.因为正三棱柱的侧面展开图是边长分别为2和4的矩形,
所以有以下两种情况:
当2是下底面的周长,4是正三棱柱的高时,
正三棱柱的表面积为;
当4是下底面的周长,2是正三棱柱的高时,
正三棱柱的表面积为;
故答案为:或.
21.(1)在正三棱锥中,SA,SB,SC两两垂直且AB=BC=CA,P为底面ABC内的一点,连接PA,PB,PC,PS,如图,可将原三棱锥分成三个三棱锥,
它们的高分别为,由,
即,
得
(2)由,得.
又,∴,∴,
当且仅当时取等号.
故当时,点P为正三角形的中心.
22.
(1)如图,做该正棱台的轴截面, 中, ,
所以 ,根据对称性, ,
故 所以 ,
正四棱台上底面是一个边长为 的正方形,
即
(2)正四棱台中,上下底面均为正方形,且侧棱长相等, 在底面的射影为 ,
所以 , 与底面所成角为 ,
,
, , .
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
