人教A版(2019)必修第一册 5.1.1 任意角 课件(共26张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册 5.1.1 任意角 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
任意角
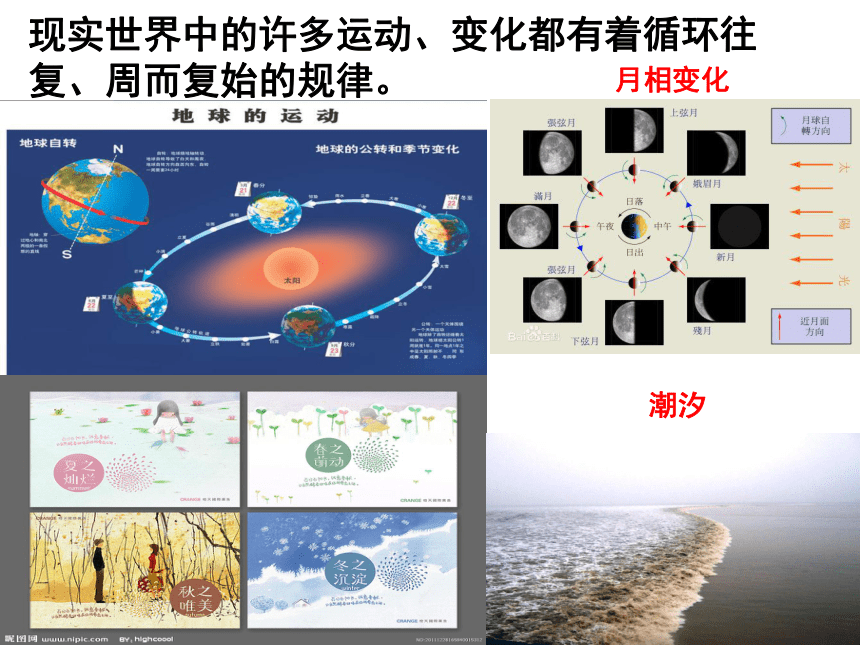
现实世界中的许多运动、变化都有着循环往复、周而复始的规律。
月相变化
潮汐
月相变化
潮汐
如何用数学的方法来刻画这种变化规律呢?
“周期性现象”
简谐运动
摩天轮
函数
一次函数模型
二次函数模型
“周期性现象”
火箭发射,高度与时间
匀速直线运动,路程与时间
三角函数模型
三角学起源于对三角形边角关系的定量考察,这始于古希腊一批天文学家对天文的测量。
三角函数是高中数学的一个重要内容,它能够简单地解决许多数学问题,在中学
数学中有着非常广泛的应用。
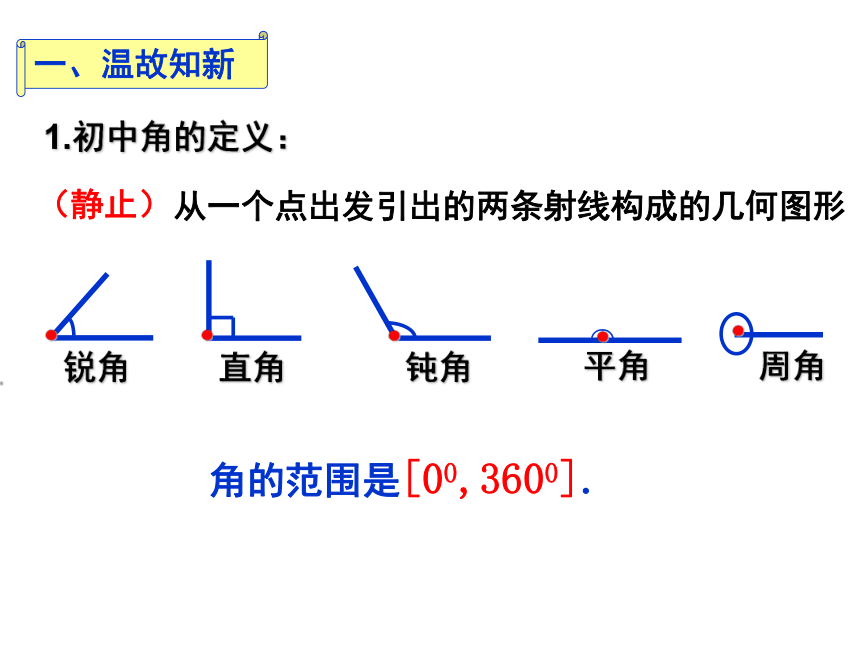
1.初中角的定义:
从一个点出发引出的两条射线构成的几何图形
一、温故知新
(静止)
锐角
直角
钝角
平角
周角
╭╮
●
●
●
●
●
角的范围是[00,3600].
这些角不仅不在范围[0 ,360 ]内,而且旋转的方向不同.
有必要将角的概念推广到任意角,
想想用什么办法才能推广到任意角?
(1)跳水运动员“前空翻或后空翻了900 .
(2)经过2小时,时针、分针、秒针转了的度数。
(3) 工人师傅在拧紧或拧松螺丝时,转动的角度
如何表示比较合适
二、设置情景
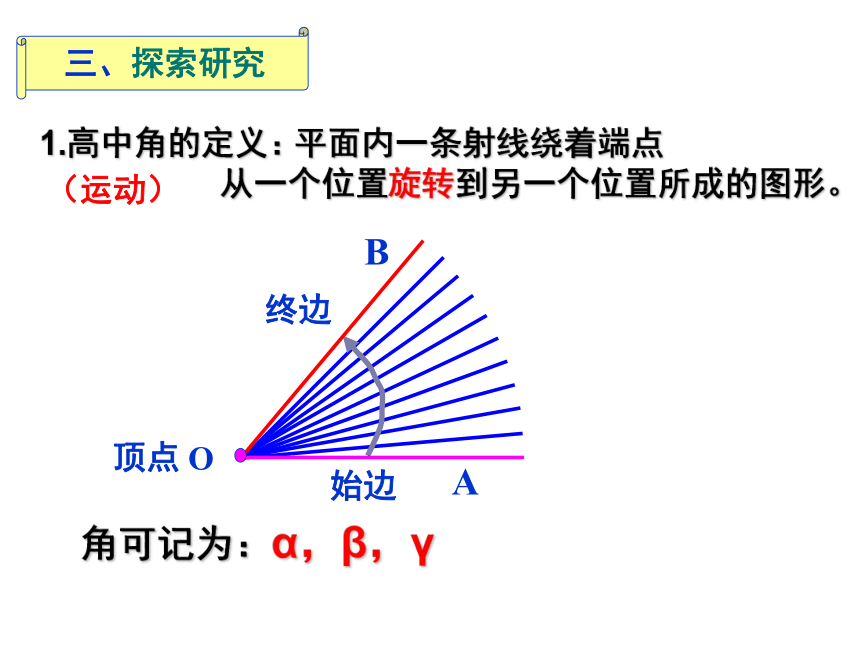
1.高中角的定义:
平面内一条射线绕着端点
从一个位置旋转到另一个位置所成的图形。
(运动)
B
终边
顶点
A
始边
O
三、探索研究
角可记为:α,β,γ
问题:
对于“大于360°的角或按不同方向旋转而成的角” 如何表示和区分这些角呢
逆时针
顺时针
正角
负角
零角
角
任意角
负角:按顺时针方向旋转而成的角;
零角:射线没有作任何旋转时的角。
正角:按逆时针方向旋转而成的角;
2、角的推广
任
意
角
三、探索研究
问:① - 30 与30 有何区别?
负角:按顺时针方向旋转而成的角;
零角:射线没有作任何旋转时的角。
正角:按逆时针方向旋转而成的角;
2、角的推广
任
意
角
三、探索研究
互为相反角:如果两个角的旋转方向相反且旋转量相等,那么这两个角就叫做互为相反角。
如果两个角的旋转方向相同且旋转量相等,那么就称两个角相等。
类比于实数运算,角的减法运算可以转化为加法运算
②钟表的指针旋转所成的角是什么角
③零角的始边与终边是重合的,
反之,始边与终边是重合的一定是零角吗?
练习1: 钟表经过4小时,时针与分针各
旋转 和 (填度数).
象限角:终边落在第几象限就是第几象限角
y
x
o
始边
终边
(1)角的顶点与坐标原点重合
(2)角的始边与X轴的非负半轴重合
为了讨论问题方便,在直角坐标系中研究角
请作出-150°,120°, 30°,-330°, 390°,750° , 270°的角。
C
D
E
B
A
Ⅰ
Ⅱ
Ⅲ
Ⅳ
轴线角:角的终边在坐标轴上的角(角的终边不在任何象限的角),则这个角不属于任何一个象限.我们称为轴角。
请同学们思考:
(2)小于900的角就是锐角吗?
小于900的角可能是零角或负角,故它不一定
是锐角。
(3)锐角就是00~900的角吗?
锐角:{θ|00<θ<900};
00~900的角:{θ|00≤θ<900}.
(1)锐角是第一象限角吗?第一象限角是锐角吗?
为什么?
请作出30°,-330°,
390°,750° 的角。
③终边相同的角有无限多个,它们相差360 的整数倍.
② k Z
3.终边相同角
所有与 角终边相同的角,连同 角在内,
可构成一个集合
说明:与 角终边相同的角的一般形式为 +k·360
① 为任意角
请作出30°,-330°,
390°,750° 的角。
y
x
o
始边
终边
[例1]:在00到3600范围内,找出与下列各角终边
相同的角,并判断他们是第几象限角
(1) 6400 (2) -1200
四、知识应用
指包含0 ,但不包含360
变式: 写出与-21°的角终边相同的角的集合S,并把S中适合不等式
O
x
y
O
x
y
O
x
y
[例2]写出终边在y轴上的角的集合(用0到360度的角表示).
分解
S2={ | =270 +k 360 ,k Z}
S1={ | =90 + k 360 ,k Z},
s={ | =k 180 +90 ,k Z}
{ | =k 180 ,k Z}
{ | =k 90 , k Z}
{ | = 45 +k 180 ,k Z}
O
x
y
O
x
y
①
②
③
变式1:用集合的形式表示象限角
第一象限的角表示为
第二象限的角表示为
第三象限的角表示为
第四象限的角表示为
{ |k 360 <{ |k 360 +90 < { |k 360 +180 < { |k 360 +270 < 或{ |k 360 -90 < 变式2 :如图,求终边在阴影部分的角的集合。
(1)
30
O
A
x
y
(2)
30
O
x
y
练习:写出如图终边落在阴影部分的角的集合。
30
O
x
y
45
30
O
A
x
y
B
45
注意:角的终边逆时针旋转由小变大
30
O
x
y
30
(3)
30
O
A
x
y
B
45
例3:如果角 是第二象限角,那么 是哪个象限角? 2 呢?
2
解:
O
x
y
45
45
1
2
3
1
2
4
4
3
图示记忆法
1、3
2、4
1、3
2、4
2.若α是第四象限角,则1800-α一定是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
例4 已知 、 有下列关系,分别求 、 之间的关系:
(1) 、 的终边关于X轴对称;
(2) 、 的终边关于Y轴对称;
(3) 、 的终边关于原点对称;
(4) 、 的终边在一条直线上。
小结与作业
(1).掌握正角,负角和零角的概念
(2).掌握象限角的概念,并会判断一个角是第几象限角
(3).掌握终边相同角的表示方法和判断方法
任意角
现实世界中的许多运动、变化都有着循环往复、周而复始的规律。
月相变化
潮汐
月相变化
潮汐
如何用数学的方法来刻画这种变化规律呢?
“周期性现象”
简谐运动
摩天轮
函数
一次函数模型
二次函数模型
“周期性现象”
火箭发射,高度与时间
匀速直线运动,路程与时间
三角函数模型
三角学起源于对三角形边角关系的定量考察,这始于古希腊一批天文学家对天文的测量。
三角函数是高中数学的一个重要内容,它能够简单地解决许多数学问题,在中学
数学中有着非常广泛的应用。
1.初中角的定义:
从一个点出发引出的两条射线构成的几何图形
一、温故知新
(静止)
锐角
直角
钝角
平角
周角
╭╮
●
●
●
●
●
角的范围是[00,3600].
这些角不仅不在范围[0 ,360 ]内,而且旋转的方向不同.
有必要将角的概念推广到任意角,
想想用什么办法才能推广到任意角?
(1)跳水运动员“前空翻或后空翻了900 .
(2)经过2小时,时针、分针、秒针转了的度数。
(3) 工人师傅在拧紧或拧松螺丝时,转动的角度
如何表示比较合适
二、设置情景
1.高中角的定义:
平面内一条射线绕着端点
从一个位置旋转到另一个位置所成的图形。
(运动)
B
终边
顶点
A
始边
O
三、探索研究
角可记为:α,β,γ
问题:
对于“大于360°的角或按不同方向旋转而成的角” 如何表示和区分这些角呢
逆时针
顺时针
正角
负角
零角
角
任意角
负角:按顺时针方向旋转而成的角;
零角:射线没有作任何旋转时的角。
正角:按逆时针方向旋转而成的角;
2、角的推广
任
意
角
三、探索研究
问:① - 30 与30 有何区别?
负角:按顺时针方向旋转而成的角;
零角:射线没有作任何旋转时的角。
正角:按逆时针方向旋转而成的角;
2、角的推广
任
意
角
三、探索研究
互为相反角:如果两个角的旋转方向相反且旋转量相等,那么这两个角就叫做互为相反角。
如果两个角的旋转方向相同且旋转量相等,那么就称两个角相等。
类比于实数运算,角的减法运算可以转化为加法运算
②钟表的指针旋转所成的角是什么角
③零角的始边与终边是重合的,
反之,始边与终边是重合的一定是零角吗?
练习1: 钟表经过4小时,时针与分针各
旋转 和 (填度数).
象限角:终边落在第几象限就是第几象限角
y
x
o
始边
终边
(1)角的顶点与坐标原点重合
(2)角的始边与X轴的非负半轴重合
为了讨论问题方便,在直角坐标系中研究角
请作出-150°,120°, 30°,-330°, 390°,750° , 270°的角。
C
D
E
B
A
Ⅰ
Ⅱ
Ⅲ
Ⅳ
轴线角:角的终边在坐标轴上的角(角的终边不在任何象限的角),则这个角不属于任何一个象限.我们称为轴角。
请同学们思考:
(2)小于900的角就是锐角吗?
小于900的角可能是零角或负角,故它不一定
是锐角。
(3)锐角就是00~900的角吗?
锐角:{θ|00<θ<900};
00~900的角:{θ|00≤θ<900}.
(1)锐角是第一象限角吗?第一象限角是锐角吗?
为什么?
请作出30°,-330°,
390°,750° 的角。
③终边相同的角有无限多个,它们相差360 的整数倍.
② k Z
3.终边相同角
所有与 角终边相同的角,连同 角在内,
可构成一个集合
说明:与 角终边相同的角的一般形式为 +k·360
① 为任意角
请作出30°,-330°,
390°,750° 的角。
y
x
o
始边
终边
[例1]:在00到3600范围内,找出与下列各角终边
相同的角,并判断他们是第几象限角
(1) 6400 (2) -1200
四、知识应用
指包含0 ,但不包含360
变式: 写出与-21°的角终边相同的角的集合S,并把S中适合不等式
O
x
y
O
x
y
O
x
y
[例2]写出终边在y轴上的角的集合(用0到360度的角表示).
分解
S2={ | =270 +k 360 ,k Z}
S1={ | =90 + k 360 ,k Z},
s={ | =k 180 +90 ,k Z}
{ | =k 180 ,k Z}
{ | =k 90 , k Z}
{ | = 45 +k 180 ,k Z}
O
x
y
O
x
y
①
②
③
变式1:用集合的形式表示象限角
第一象限的角表示为
第二象限的角表示为
第三象限的角表示为
第四象限的角表示为
{ |k 360 <
(1)
30
O
A
x
y
(2)
30
O
x
y
练习:写出如图终边落在阴影部分的角的集合。
30
O
x
y
45
30
O
A
x
y
B
45
注意:角的终边逆时针旋转由小变大
30
O
x
y
30
(3)
30
O
A
x
y
B
45
例3:如果角 是第二象限角,那么 是哪个象限角? 2 呢?
2
解:
O
x
y
45
45
1
2
3
1
2
4
4
3
图示记忆法
1、3
2、4
1、3
2、4
2.若α是第四象限角,则1800-α一定是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
例4 已知 、 有下列关系,分别求 、 之间的关系:
(1) 、 的终边关于X轴对称;
(2) 、 的终边关于Y轴对称;
(3) 、 的终边关于原点对称;
(4) 、 的终边在一条直线上。
小结与作业
(1).掌握正角,负角和零角的概念
(2).掌握象限角的概念,并会判断一个角是第几象限角
(3).掌握终边相同角的表示方法和判断方法
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
