人教A版(2019)必修第一册 5.1.2 弧度制 课件(共29张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册 5.1.2 弧度制 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 399.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 06:51:10 | ||
图片预览







文档简介
(共29张PPT)
5.1.2 弧度制
一.复习填空:
O
x
y
45
45
1
2
3
1
2
4
4
3
引言:
度量长度可以用米、英尺、公里的不同的单位制,度量重量可以用千克、磅、吨等不同单位制,不同的单位制可以给解决问题带来方便,初中时,角是用什么单位度量的呢?
在角度制下,当把两个带着度、分、秒各单位的角相加、相减时,由于运算进率非十进制,总给我们带来不少困难.那么我们能否重新选择角单位,使在该单位制下两角的加、减运算与常规的十进制加减法一样去做呢?
角度制的单位有:度、分、秒。
1、角度制
用“度”作单位来度量角的单位制称作 “角度制”,规定:圆周1/360的圆心角称作1°角。
弧度制
60进制
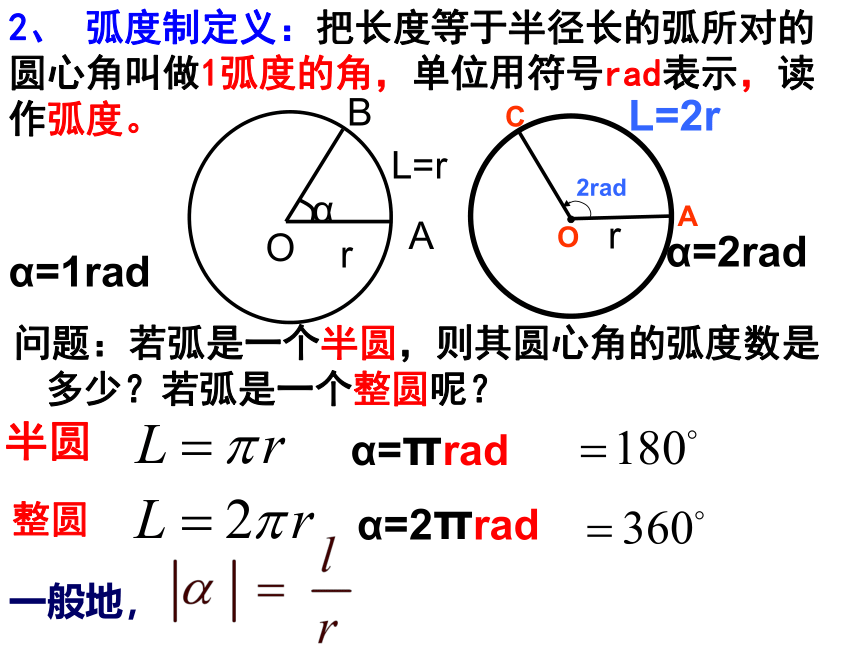
2、 弧度制定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,单位用符号rad表示,读作弧度。
α=1rad
问题:若弧是一个半圆,则其圆心角的弧度数是多少?若弧是一个整圆呢?
B
α
L=r
A
O
r
O
A
C
L=2r
2rad
r
α=2rad
半圆
整圆
α=πrad
α=2πrad
一般地,
为什么可以用弧长与其半径的比值来度量角的大小呢?即这个比值是否与所取的圆的半径大小无关呢?
B
α
A
O
r
A’
B’
r’
练习 :在半径不等的两个圆内,1弧度的圆心角( )
A.所对弧长相等
B.所对的弦长相等
C.所对弧长等于各自半径
D.所对的弧长为
C
角度制与弧度制的互换:
(1)把角度换成弧度
(2)把弧度换成角度
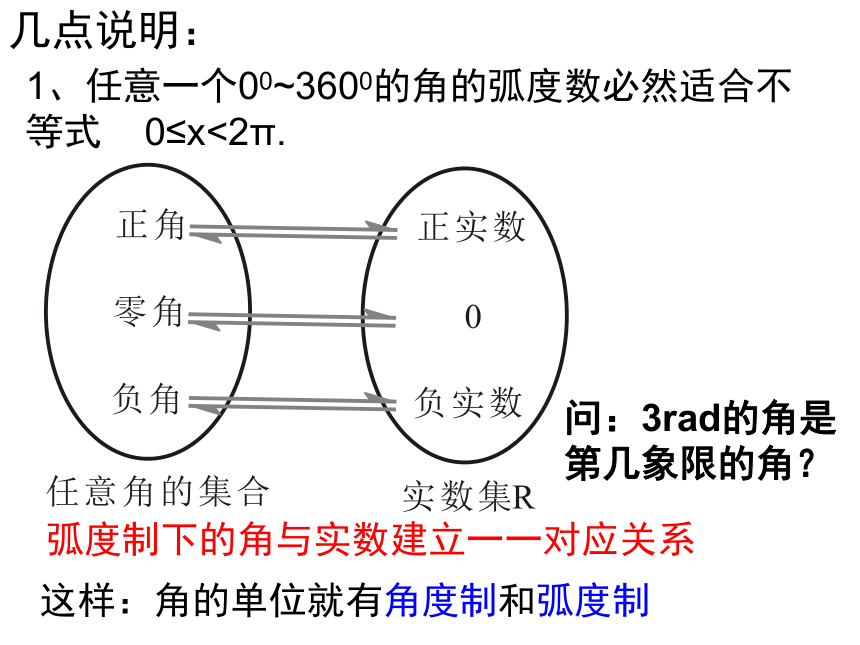
1、任意一个00~3600的角的弧度数必然适合不等式 0≤x<2π.
这样:角的单位就有角度制和弧度制
几点说明:
弧度制下的角与实数建立一一对应关系
问:3rad的角是第几象限的角?
3、例题讲解
解:∵
把 化成弧度。
例1:
∴
把 化成度。
例2:
解:
角度制与弧度制互化的关键:
角度
弧度
0
练习1:写出一些特殊角的弧度数
O
x
y
练习
1)用弧度制写出与300同终边的角的集合;
2)用弧度制写出第四象限角的集合;
3)用弧度制表示 坐标轴上角的集合;
4)指出下列用弧度制表示的角是第几象限角
注意:弧度数来表示或角度来表示,不可混用于一式中。
例4:利用弧度制证明下列关于扇形的公式
小结:
1、弧度制的意义——角与实数一一对应;
3、弧度制下的弧长公式、扇形面积公式及应用
2、换算公式及方法;
学后反思
一一对应关系,同时也揭示了圆中弧长与半径之间的
1、弧度制的引进,使“角度”与“实数”之间建立了
关系,即弧长公式:l=|α|r
2、弧度制下的弧长公式为l=|α|r;扇形面积公式为
在角度制下则是
这里,α,n分别是圆心角的弧度数与角度数,R为圆
的半径。
3、在具体求弧长和扇形面积时,弧度制下的弧长
公式及扇形面积公式既形式简单又便于计算,但要
注意适用条件是在弧度制下,角的单位要统一,都用
弧度数来表示或角度来表示,不可混用于一式中。
应用1:如图,扇形AOB的面积为4cm2,周长为10cm,求扇形的中心角α及AB的长。
B
A
O
解:设扇形半径为r,
应用2:已知扇形的周长为20cm,当扇形的中心角为多少时,它有最大面积?
解:设扇形的弧长为L,半径为R,由已知条件
L+2R=20,即L=20-2R。
由0扇形面积为S=
当R=5时,S最大,此时L=10
时它有最大面积。
变式:已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是多少?
这个圆心角所夹扇形的面积是多少?
该弧所在的弓形面积是多少?
变式:已知扇形面积为S(S>0),当扇形的圆心角为多少弧度时,它的周长最小?
解:
扇形周长
∴m的最小值为
此时
由对勾函数的单调性知
9.已知 、 有下列关系,分别求 、 之间的关系:
(1) 、 的终边关于X轴对称;
(2) 、 的终边关于Y轴对称;
(3) 、 的终边关于原点对称;
(4) 、 的终边在一条直线上。
随堂练习
1、圆的半径变为原来的2倍,而弧长也增加到原来的2倍,则
A、扇形的面积不变
B、扇形的圆心角不变
C、扇形的面积增大到原来的2倍
D、扇形的圆心角增大到原来的2倍
B
2、时钟经过一小时,时针转过
B
3、已知扇形周长为6cm,面积为2cm2,则扇形圆心角的弧度数为
A、1 B、4 C、1或4 D、2或4
C
4、当圆心角α=-216o,弧长L=7πcm时,其半径r=________
5、在半径为 的圆中,圆心角为周角的 的角所对圆弧的长为___________
40
6、若2 rad的圆心角所对的弧长是4cm,则这个圆心角所在扇形的面积为_________
4cm2
7. 在半径为R的圆中,240 的中心角所对的弧长为 ,面积为2R2的扇形的中心角等于 弧度。
解:(1)240 = ,根据l=αR,得
(2)根据S= lR= αR2,且S=2R2.
所以 α=4.
8. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?
解:周长=2πR=2R+l,所以l=2(π-1)R.
所以扇形的中心角是2(π-1) rad.
合( )
扇形面积是
学后反思
一一对应关系,同时也揭示了圆中弧长与半径之间的
1、弧度制的引进,使“角度”与“实数”之间建立了
关系,即弧长公式:l=|α|r
2、弧度制下的弧长公式为l=|α|r;扇形面积公式为
在角度制下则是
这里,α,n分别是圆心角的弧度数与角度数,R为圆
的半径。
3、在具体求弧长和扇形面积时,弧度制下的弧长
公式及扇形面积公式既形式简单又便于计算,但要
注意适用条件是在弧度制下,角的单位要统一,都用
弧度数来表示或角度来表示,不可混用于一式中。
5.1.2 弧度制
一.复习填空:
O
x
y
45
45
1
2
3
1
2
4
4
3
引言:
度量长度可以用米、英尺、公里的不同的单位制,度量重量可以用千克、磅、吨等不同单位制,不同的单位制可以给解决问题带来方便,初中时,角是用什么单位度量的呢?
在角度制下,当把两个带着度、分、秒各单位的角相加、相减时,由于运算进率非十进制,总给我们带来不少困难.那么我们能否重新选择角单位,使在该单位制下两角的加、减运算与常规的十进制加减法一样去做呢?
角度制的单位有:度、分、秒。
1、角度制
用“度”作单位来度量角的单位制称作 “角度制”,规定:圆周1/360的圆心角称作1°角。
弧度制
60进制
2、 弧度制定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,单位用符号rad表示,读作弧度。
α=1rad
问题:若弧是一个半圆,则其圆心角的弧度数是多少?若弧是一个整圆呢?
B
α
L=r
A
O
r
O
A
C
L=2r
2rad
r
α=2rad
半圆
整圆
α=πrad
α=2πrad
一般地,
为什么可以用弧长与其半径的比值来度量角的大小呢?即这个比值是否与所取的圆的半径大小无关呢?
B
α
A
O
r
A’
B’
r’
练习 :在半径不等的两个圆内,1弧度的圆心角( )
A.所对弧长相等
B.所对的弦长相等
C.所对弧长等于各自半径
D.所对的弧长为
C
角度制与弧度制的互换:
(1)把角度换成弧度
(2)把弧度换成角度
1、任意一个00~3600的角的弧度数必然适合不等式 0≤x<2π.
这样:角的单位就有角度制和弧度制
几点说明:
弧度制下的角与实数建立一一对应关系
问:3rad的角是第几象限的角?
3、例题讲解
解:∵
把 化成弧度。
例1:
∴
把 化成度。
例2:
解:
角度制与弧度制互化的关键:
角度
弧度
0
练习1:写出一些特殊角的弧度数
O
x
y
练习
1)用弧度制写出与300同终边的角的集合;
2)用弧度制写出第四象限角的集合;
3)用弧度制表示 坐标轴上角的集合;
4)指出下列用弧度制表示的角是第几象限角
注意:弧度数来表示或角度来表示,不可混用于一式中。
例4:利用弧度制证明下列关于扇形的公式
小结:
1、弧度制的意义——角与实数一一对应;
3、弧度制下的弧长公式、扇形面积公式及应用
2、换算公式及方法;
学后反思
一一对应关系,同时也揭示了圆中弧长与半径之间的
1、弧度制的引进,使“角度”与“实数”之间建立了
关系,即弧长公式:l=|α|r
2、弧度制下的弧长公式为l=|α|r;扇形面积公式为
在角度制下则是
这里,α,n分别是圆心角的弧度数与角度数,R为圆
的半径。
3、在具体求弧长和扇形面积时,弧度制下的弧长
公式及扇形面积公式既形式简单又便于计算,但要
注意适用条件是在弧度制下,角的单位要统一,都用
弧度数来表示或角度来表示,不可混用于一式中。
应用1:如图,扇形AOB的面积为4cm2,周长为10cm,求扇形的中心角α及AB的长。
B
A
O
解:设扇形半径为r,
应用2:已知扇形的周长为20cm,当扇形的中心角为多少时,它有最大面积?
解:设扇形的弧长为L,半径为R,由已知条件
L+2R=20,即L=20-2R。
由0
当R=5时,S最大,此时L=10
时它有最大面积。
变式:已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是多少?
这个圆心角所夹扇形的面积是多少?
该弧所在的弓形面积是多少?
变式:已知扇形面积为S(S>0),当扇形的圆心角为多少弧度时,它的周长最小?
解:
扇形周长
∴m的最小值为
此时
由对勾函数的单调性知
9.已知 、 有下列关系,分别求 、 之间的关系:
(1) 、 的终边关于X轴对称;
(2) 、 的终边关于Y轴对称;
(3) 、 的终边关于原点对称;
(4) 、 的终边在一条直线上。
随堂练习
1、圆的半径变为原来的2倍,而弧长也增加到原来的2倍,则
A、扇形的面积不变
B、扇形的圆心角不变
C、扇形的面积增大到原来的2倍
D、扇形的圆心角增大到原来的2倍
B
2、时钟经过一小时,时针转过
B
3、已知扇形周长为6cm,面积为2cm2,则扇形圆心角的弧度数为
A、1 B、4 C、1或4 D、2或4
C
4、当圆心角α=-216o,弧长L=7πcm时,其半径r=________
5、在半径为 的圆中,圆心角为周角的 的角所对圆弧的长为___________
40
6、若2 rad的圆心角所对的弧长是4cm,则这个圆心角所在扇形的面积为_________
4cm2
7. 在半径为R的圆中,240 的中心角所对的弧长为 ,面积为2R2的扇形的中心角等于 弧度。
解:(1)240 = ,根据l=αR,得
(2)根据S= lR= αR2,且S=2R2.
所以 α=4.
8. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?
解:周长=2πR=2R+l,所以l=2(π-1)R.
所以扇形的中心角是2(π-1) rad.
合( )
扇形面积是
学后反思
一一对应关系,同时也揭示了圆中弧长与半径之间的
1、弧度制的引进,使“角度”与“实数”之间建立了
关系,即弧长公式:l=|α|r
2、弧度制下的弧长公式为l=|α|r;扇形面积公式为
在角度制下则是
这里,α,n分别是圆心角的弧度数与角度数,R为圆
的半径。
3、在具体求弧长和扇形面积时,弧度制下的弧长
公式及扇形面积公式既形式简单又便于计算,但要
注意适用条件是在弧度制下,角的单位要统一,都用
弧度数来表示或角度来表示,不可混用于一式中。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
