人教A版(2019)选修第一册 3.1.2 椭圆的简单几何性质 课件(共22张PPT)
文档属性
| 名称 | 人教A版(2019)选修第一册 3.1.2 椭圆的简单几何性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 07:36:28 | ||
图片预览






文档简介
3.1.2 椭圆的简单几何性质
第三章 圆锥曲线
学习目标
1.椭圆的定义:
平面内与两个定点????????、????????的距离之和为常数(大于|????????????????|)的动点????的轨迹叫做椭圆.
?
2.椭圆的标准方程:
3.椭圆中????,????,????的关系:
?
当焦点在x轴上时
当焦点在y轴上时
????????=????????+???????? (????>????>????)
?
这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距。
复习回回顾
设点M的坐标为(x, y),点P的坐标为(x0, y0),则点D的坐标为(x0, 0).
由点M是线段PD的中点,得
例2 如图,在圆 上任意一点P , 过点P作x轴的垂线段 PD, D为垂足. 当点P在圆上运动时, 线段 PD中点M的轨迹方程是什么?为什么?
x
y
P
M
O
?
D
?
解:(相关点代入法)
例3
x
y
B
M
O
A
?
解: 设点M (x, y),由A(-5, 0), B(5, 0),可得
新知探索
l
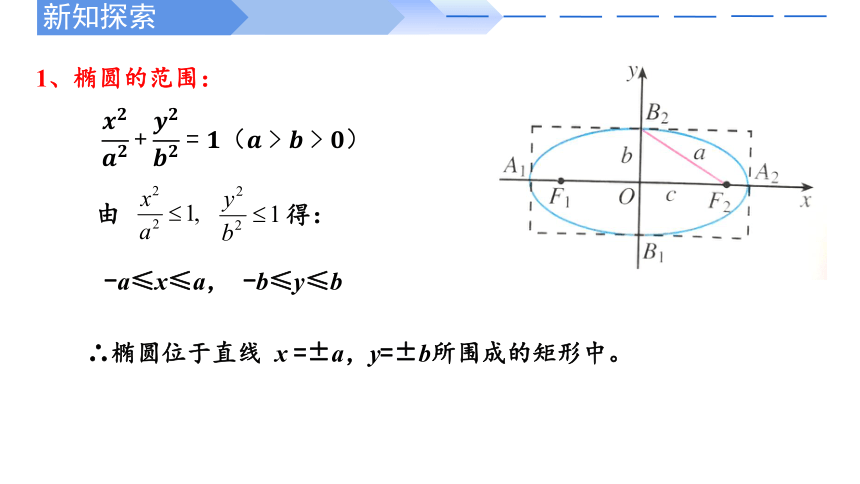
1、椭圆的范围:
由 得:
-a≤x≤a, -b≤y≤b
∴椭圆位于直线 x =±a,y=±b所围成的矩形中。
????????????????+????????????????=????(????>????>????)
?
新知探索
l
l
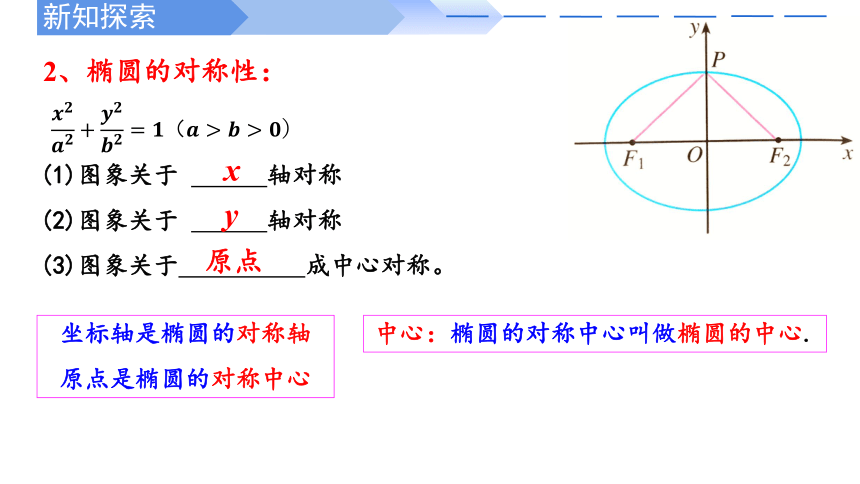
2、椭圆的对称性:
(1)图象关于 轴对称
(2)图象关于 轴对称
(3)图象关于 成中心对称。
y
x
原点
坐标轴是椭圆的对称轴
原点是椭圆的对称中心
中心:椭圆的对称中心叫做椭圆的中心.
????????????????+????????????????=????(????>????>????)
?
新知探索
3、椭圆的顶点:
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
椭圆顶点坐标:????????(?????,????)、????????(????,????)、????????(????,?????)、????????(????,????)
?
长轴:线段A1A2 长轴长:|A1A2|=2a 长半轴长:a
短轴:线段B1B2 短轴长:|B1B2|=2b 短半轴长:b
????????????????+????????????????=????(????>????>????)
?
新知探索
l
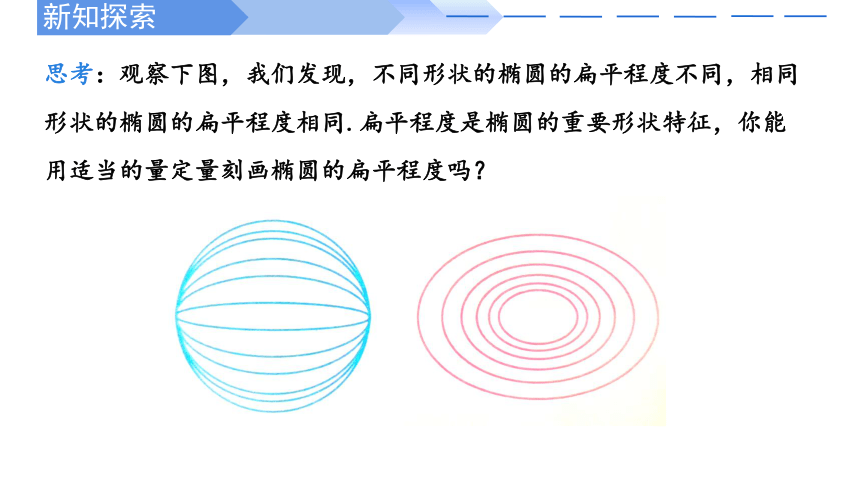
思考:观察下图,我们发现,不同形状的椭圆的扁平程度不同,相同形状的椭圆的扁平程度相同.扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗?
l
4、离心率
如图, 椭圆 的长
半轴为a, 半焦距为c.
利用信息技术,保持长半轴a不变,改变椭圆的半焦距c,
可以发现,c越接近a,椭圆越扁平. 类似的,保持c不变,改变a的大小,则a越接近c,椭圆越扁平;而当a, c扩大或缩小相同倍数时,椭圆的形状不变.
这样, 利用a和c这两个量, 可以刻画椭圆的扁平程度.
?
离心率越大,椭圆越扁
离心率越小,椭圆越圆
注:因为在椭圆中,????2=????2+????2,所以????=????????=(????????)2=????2?????2????2=1?????2????2.
?
椭圆的简单几何性质
例题
题型一:由椭圆的标准方程研究其几何性质用
例1.求椭圆9????2+16????2=144的长轴长、短轴长、离心率、焦点和顶点坐标,并画出图形。
?
椭圆的长轴长2????=8,短轴长2????=6,离心率????=????????=74,
两个焦点坐标分别是????1(?7,0)和????2(7,0),
四个顶点坐标分别是????1(?4,0),????2(4,0),????1(0,?3)和????2(0,3).
?
解:把原方程化为标准方程为????216+????29=1,
?
于是????=4,????=3,????=16?9=7,
?
例题
题型二:利用几何性质求椭圆的标准方程
例2.求适合下列条件的椭圆的标准方程.
(1)长轴长是10,离心率是45;
?
解(1):设椭圆方程为????2????2+????2????2=1(????>????>0)或????2????2+????2????2=1(????>????>0).
由已知得2????=10,????=5.
?
又∵????=????????=45,∴????=4.
∴????2=????2?????2=9.
∴椭圆方程为????225+????29=1或????225+????29=1.
?
(2)在????轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
?
例题
(2)在????轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
?
解(2):依题意可设椭圆方程为????2????2+????2????2=1(????>????>0).
如图所示,?????1????????2为等腰直角三角形,
|????????|=????,|????????2|=????,
则????=????=3,????2=????2+????2=18,
故所求椭圆的方程为????218+????29=1.
?
B2
B1
练习
题型三:椭圆离心率的求法及应用
例3.(2018年全卷Ⅱ)已知????1,????2是椭圆????的两个焦点,????是上????的一点.若????????1⊥????????2,且∠????????2????1=60°,则????的离心率为( ).
A.1?32 B.2?3 C.3?12 D.3?1
?
D
y
O
F1
F2
P
x
练习
变式:如图,设椭圆的左、右焦点分别为F1,F2,过F1作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,求椭圆的离心率.
椭圆的通径:过焦点垂直于长轴的直线与椭圆相交所得的线段长度,椭圆的通径长为
y
O
F1
F2
P
x
解:
由已知可得,
y
O
F1
F2
P
x
解得
证明:
椭圆的焦点三角形面积公式:
y
O
F1
F2
P
x
法2:
【练习】1、
2、
3
椭圆的简单几何性质
课堂小结
第三章 圆锥曲线
学习目标
1.椭圆的定义:
平面内与两个定点????????、????????的距离之和为常数(大于|????????????????|)的动点????的轨迹叫做椭圆.
?
2.椭圆的标准方程:
3.椭圆中????,????,????的关系:
?
当焦点在x轴上时
当焦点在y轴上时
????????=????????+???????? (????>????>????)
?
这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距。
复习回回顾
设点M的坐标为(x, y),点P的坐标为(x0, y0),则点D的坐标为(x0, 0).
由点M是线段PD的中点,得
例2 如图,在圆 上任意一点P , 过点P作x轴的垂线段 PD, D为垂足. 当点P在圆上运动时, 线段 PD中点M的轨迹方程是什么?为什么?
x
y
P
M
O
?
D
?
解:(相关点代入法)
例3
x
y
B
M
O
A
?
解: 设点M (x, y),由A(-5, 0), B(5, 0),可得
新知探索
l
1、椭圆的范围:
由 得:
-a≤x≤a, -b≤y≤b
∴椭圆位于直线 x =±a,y=±b所围成的矩形中。
????????????????+????????????????=????(????>????>????)
?
新知探索
l
l
2、椭圆的对称性:
(1)图象关于 轴对称
(2)图象关于 轴对称
(3)图象关于 成中心对称。
y
x
原点
坐标轴是椭圆的对称轴
原点是椭圆的对称中心
中心:椭圆的对称中心叫做椭圆的中心.
????????????????+????????????????=????(????>????>????)
?
新知探索
3、椭圆的顶点:
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
椭圆顶点坐标:????????(?????,????)、????????(????,????)、????????(????,?????)、????????(????,????)
?
长轴:线段A1A2 长轴长:|A1A2|=2a 长半轴长:a
短轴:线段B1B2 短轴长:|B1B2|=2b 短半轴长:b
????????????????+????????????????=????(????>????>????)
?
新知探索
l
思考:观察下图,我们发现,不同形状的椭圆的扁平程度不同,相同形状的椭圆的扁平程度相同.扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗?
l
4、离心率
如图, 椭圆 的长
半轴为a, 半焦距为c.
利用信息技术,保持长半轴a不变,改变椭圆的半焦距c,
可以发现,c越接近a,椭圆越扁平. 类似的,保持c不变,改变a的大小,则a越接近c,椭圆越扁平;而当a, c扩大或缩小相同倍数时,椭圆的形状不变.
这样, 利用a和c这两个量, 可以刻画椭圆的扁平程度.
?
离心率越大,椭圆越扁
离心率越小,椭圆越圆
注:因为在椭圆中,????2=????2+????2,所以????=????????=(????????)2=????2?????2????2=1?????2????2.
?
椭圆的简单几何性质
例题
题型一:由椭圆的标准方程研究其几何性质用
例1.求椭圆9????2+16????2=144的长轴长、短轴长、离心率、焦点和顶点坐标,并画出图形。
?
椭圆的长轴长2????=8,短轴长2????=6,离心率????=????????=74,
两个焦点坐标分别是????1(?7,0)和????2(7,0),
四个顶点坐标分别是????1(?4,0),????2(4,0),????1(0,?3)和????2(0,3).
?
解:把原方程化为标准方程为????216+????29=1,
?
于是????=4,????=3,????=16?9=7,
?
例题
题型二:利用几何性质求椭圆的标准方程
例2.求适合下列条件的椭圆的标准方程.
(1)长轴长是10,离心率是45;
?
解(1):设椭圆方程为????2????2+????2????2=1(????>????>0)或????2????2+????2????2=1(????>????>0).
由已知得2????=10,????=5.
?
又∵????=????????=45,∴????=4.
∴????2=????2?????2=9.
∴椭圆方程为????225+????29=1或????225+????29=1.
?
(2)在????轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
?
例题
(2)在????轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
?
解(2):依题意可设椭圆方程为????2????2+????2????2=1(????>????>0).
如图所示,?????1????????2为等腰直角三角形,
|????????|=????,|????????2|=????,
则????=????=3,????2=????2+????2=18,
故所求椭圆的方程为????218+????29=1.
?
B2
B1
练习
题型三:椭圆离心率的求法及应用
例3.(2018年全卷Ⅱ)已知????1,????2是椭圆????的两个焦点,????是上????的一点.若????????1⊥????????2,且∠????????2????1=60°,则????的离心率为( ).
A.1?32 B.2?3 C.3?12 D.3?1
?
D
y
O
F1
F2
P
x
练习
变式:如图,设椭圆的左、右焦点分别为F1,F2,过F1作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,求椭圆的离心率.
椭圆的通径:过焦点垂直于长轴的直线与椭圆相交所得的线段长度,椭圆的通径长为
y
O
F1
F2
P
x
解:
由已知可得,
y
O
F1
F2
P
x
解得
证明:
椭圆的焦点三角形面积公式:
y
O
F1
F2
P
x
法2:
【练习】1、
2、
3
椭圆的简单几何性质
课堂小结
