人教版(2019)必修第三册 9.2 库仑定律 课件(16张PPT)
文档属性
| 名称 | 人教版(2019)必修第三册 9.2 库仑定律 课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 282.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-19 13:37:17 | ||
图片预览





文档简介
(共16张PPT)
库仑定律
2
2
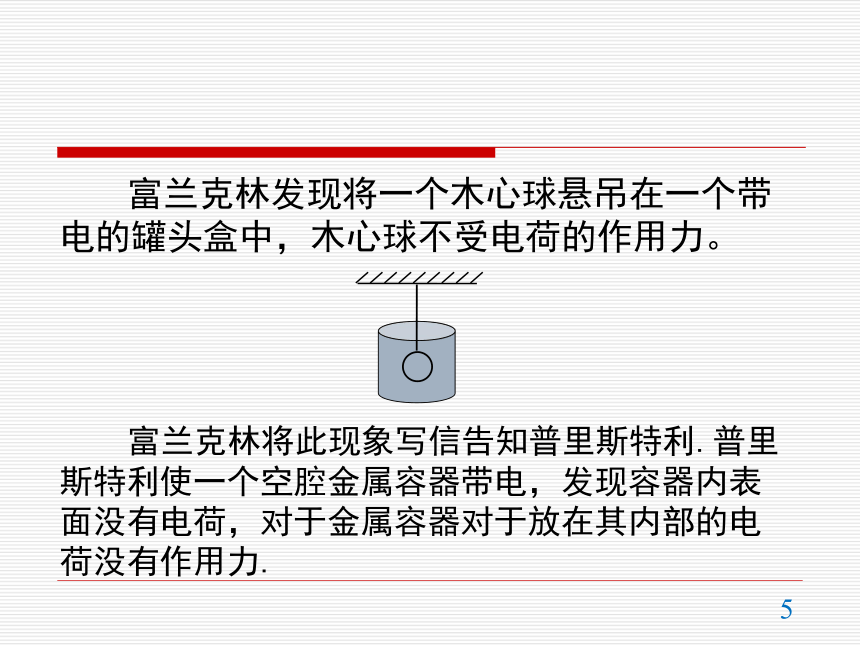
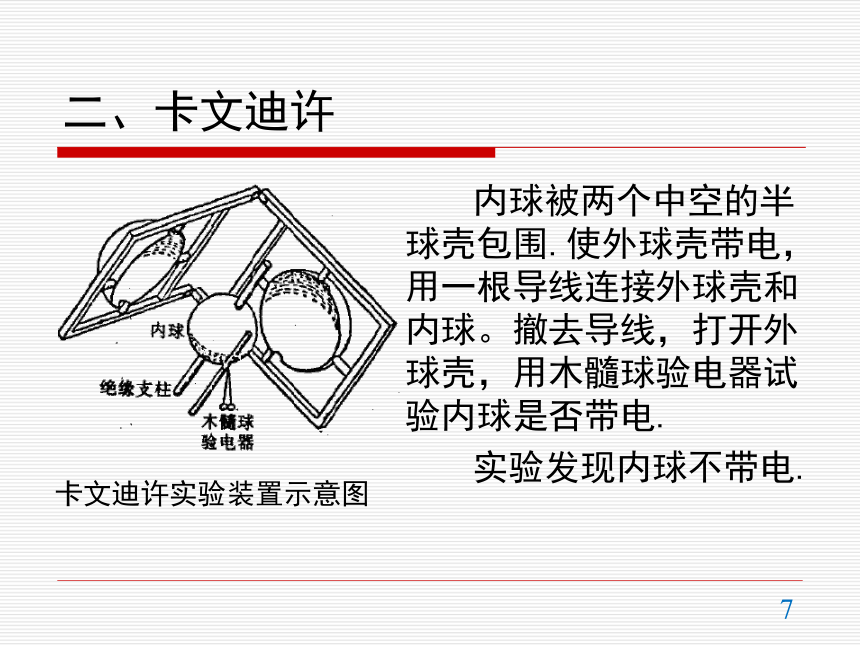
18世纪中叶以后,在已认识同种电荷相斥,异种电荷相吸基础上,不少学者对电荷间的相互作用力规律进行了猜测和实验探索.牛顿力学取得很大的成功,当时的电学家米谢尔、普里斯特利、卡文迪许和库仑等人类比引力定律猜测电力亦遵循平方反比定律.法国科学家库仑通过扭力称实验给予平方反比律严格的实验基础.库仑以其精妙的实验技巧和对物理学的贡献名垂科学史.约1750年,德国柏林科学院院士爱皮努斯发现两带电体之间的距离缩短时,两者之间的吸引力或排斥力明显增加,但没有继续研究下去.大约1760年,丹尼尔·伯努利从牛顿力学自然观出发,猜测电力跟万有引力一样,服从平方反比定律.其想法具有一定的代表性,引力平方反比定律早已确立,对人们的自然观具有深刻的影响。一、普里斯特利的贡献普里斯特利是英国著名物理学家,氧的发现者,第一个提出电力与距离平方成反比。1767年出版《电学的历史和现状及其原始实验》,是科学史上的第一部电学史,总结了前人和当时重要的电学发现。普里斯特利在研究富兰克林的一个实验中提出了电力平方反比律。富兰克林发现将一个木心球悬吊在一个带电的罐头盒中,木心球不受电荷的作用力。富兰克林将此现象写信告知普里斯特利.普里斯特利使一个空腔金属容器带电,发现容器内表面没有电荷,对于金属容器对于放在其内部的电荷没有作用力.“难道我们不能从这个实验推出这样的结论,即电吸引力作用服从于与万有引力相同的定律,从而也就是服从距离平方的反比定律吗 因为假如地球像一个壳体那样,就不难证明在它里面的物体受到一边的吸引不会大于来自另一边的吸引”二、卡文迪许卡文迪许实验装置示意图内球被两个中空的半球壳包围.使外球壳带电,用一根导线连接外球壳和内球。撤去导线,打开外球壳,用木髓球验电器试验内球是否带电.实验发现内球不带电.卡文迪许通过实验到结论:电荷间作用力与距离的(2±1/50)次方成反比.由于实验仪器简陋,卡文迪许实验的精度并不高,但却是精确验证电力平方反比律的起点.后来英国科学家麦克斯韦(J.C.Maxwell,1831-1879)将卡文迪许实验进行改进,重做实验,实验精度提高3个数量级.库仑在论文中列举一组数据,两小球相距36个刻度、18个刻度和8.5个刻度,即间距大体上是1:1/2:1/4,得到银丝分别扭转了36个刻度、144个刻度和576个刻度,即电力约为1:22:42.库仑得出“带同号电荷的两球之间的斥力,与两球中心之间距离的平方成反比”的结论。振荡电扭称实验在可活动挂码下用蚕丝悬吊一根针,针的一头固定一片金箔圆盘.圆盘前方正对一带电球,直径1英尺.库仑测得距离分别为9、18、24英寸时,摆动15次时间分别为20、41、60秒,证明振荡周期与距离基本成正比。而力与振荡周期的平方成反比,所以电吸引力与距离平方成反比。类比方法的应用库仑类比万有引力定律与质量乘积成正比,认为电力与电荷的乘积成正比,认为“假说的前一部分无需证明”.电力与距离的平方成反比也受到万有引力的启发.带电球壳对内部电荷没有电力作用、电荷分布在外表面和球壳对内部物体没有引力都强烈启发了当时的电学家。当时的科学家把引力定律和超距作用的哲学自然观用于电学和磁学。四、库仑定律真空中两个静止点电荷之间的相互作用力,与它们的电荷量的乘积成正比,与它们距离的二次方成反比,作用力的方向在它们的连线上.k=9.0×109N·m2/C2.点电荷是理想化的模型,当带电体自身大小远小于带电体间的距离,可以把带电体当作点电荷.叠加原理实验发现:两个点电荷之间的作用力不因第三个点电荷的存在而改变.两个或两个以上点电荷对某一个点电荷的作用力,等于各点电荷单独对这个电荷作用力的矢量和.【例1】试计算质子与电子间的静电力与万有引力的比值.【例2】两带正电均为Q的点电荷位于(-a,0)和(a,0).求位于(0,y)处点电荷q所受的静电力.qQQyF电练习两点电荷带电分别为+Q和-Q,位于(-a,0)和(a,0).求位于(0,y)处点电荷q所受的静电力表达式,定性画出电力的变化图像。
库仑定律
2
2
18世纪中叶以后,在已认识同种电荷相斥,异种电荷相吸基础上,不少学者对电荷间的相互作用力规律进行了猜测和实验探索.牛顿力学取得很大的成功,当时的电学家米谢尔、普里斯特利、卡文迪许和库仑等人类比引力定律猜测电力亦遵循平方反比定律.法国科学家库仑通过扭力称实验给予平方反比律严格的实验基础.库仑以其精妙的实验技巧和对物理学的贡献名垂科学史.约1750年,德国柏林科学院院士爱皮努斯发现两带电体之间的距离缩短时,两者之间的吸引力或排斥力明显增加,但没有继续研究下去.大约1760年,丹尼尔·伯努利从牛顿力学自然观出发,猜测电力跟万有引力一样,服从平方反比定律.其想法具有一定的代表性,引力平方反比定律早已确立,对人们的自然观具有深刻的影响。一、普里斯特利的贡献普里斯特利是英国著名物理学家,氧的发现者,第一个提出电力与距离平方成反比。1767年出版《电学的历史和现状及其原始实验》,是科学史上的第一部电学史,总结了前人和当时重要的电学发现。普里斯特利在研究富兰克林的一个实验中提出了电力平方反比律。富兰克林发现将一个木心球悬吊在一个带电的罐头盒中,木心球不受电荷的作用力。富兰克林将此现象写信告知普里斯特利.普里斯特利使一个空腔金属容器带电,发现容器内表面没有电荷,对于金属容器对于放在其内部的电荷没有作用力.“难道我们不能从这个实验推出这样的结论,即电吸引力作用服从于与万有引力相同的定律,从而也就是服从距离平方的反比定律吗 因为假如地球像一个壳体那样,就不难证明在它里面的物体受到一边的吸引不会大于来自另一边的吸引”二、卡文迪许卡文迪许实验装置示意图内球被两个中空的半球壳包围.使外球壳带电,用一根导线连接外球壳和内球。撤去导线,打开外球壳,用木髓球验电器试验内球是否带电.实验发现内球不带电.卡文迪许通过实验到结论:电荷间作用力与距离的(2±1/50)次方成反比.由于实验仪器简陋,卡文迪许实验的精度并不高,但却是精确验证电力平方反比律的起点.后来英国科学家麦克斯韦(J.C.Maxwell,1831-1879)将卡文迪许实验进行改进,重做实验,实验精度提高3个数量级.库仑在论文中列举一组数据,两小球相距36个刻度、18个刻度和8.5个刻度,即间距大体上是1:1/2:1/4,得到银丝分别扭转了36个刻度、144个刻度和576个刻度,即电力约为1:22:42.库仑得出“带同号电荷的两球之间的斥力,与两球中心之间距离的平方成反比”的结论。振荡电扭称实验在可活动挂码下用蚕丝悬吊一根针,针的一头固定一片金箔圆盘.圆盘前方正对一带电球,直径1英尺.库仑测得距离分别为9、18、24英寸时,摆动15次时间分别为20、41、60秒,证明振荡周期与距离基本成正比。而力与振荡周期的平方成反比,所以电吸引力与距离平方成反比。类比方法的应用库仑类比万有引力定律与质量乘积成正比,认为电力与电荷的乘积成正比,认为“假说的前一部分无需证明”.电力与距离的平方成反比也受到万有引力的启发.带电球壳对内部电荷没有电力作用、电荷分布在外表面和球壳对内部物体没有引力都强烈启发了当时的电学家。当时的科学家把引力定律和超距作用的哲学自然观用于电学和磁学。四、库仑定律真空中两个静止点电荷之间的相互作用力,与它们的电荷量的乘积成正比,与它们距离的二次方成反比,作用力的方向在它们的连线上.k=9.0×109N·m2/C2.点电荷是理想化的模型,当带电体自身大小远小于带电体间的距离,可以把带电体当作点电荷.叠加原理实验发现:两个点电荷之间的作用力不因第三个点电荷的存在而改变.两个或两个以上点电荷对某一个点电荷的作用力,等于各点电荷单独对这个电荷作用力的矢量和.【例1】试计算质子与电子间的静电力与万有引力的比值.【例2】两带正电均为Q的点电荷位于(-a,0)和(a,0).求位于(0,y)处点电荷q所受的静电力.qQQyF电练习两点电荷带电分别为+Q和-Q,位于(-a,0)和(a,0).求位于(0,y)处点电荷q所受的静电力表达式,定性画出电力的变化图像。
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
