人教版(2019)选修第二册 1.4 质谱仪与回旋加速器 课件(共31张PPT)
文档属性
| 名称 | 人教版(2019)选修第二册 1.4 质谱仪与回旋加速器 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-19 13:50:17 | ||
图片预览









文档简介
(共31张PPT)
第一章 安培力与洛伦兹力
1.4 质谱仪与回旋加速器
在科学研究和工业生产中,常需要将一束带等量电荷的粒子分开,以便知道其中所含物质的成分。利用所学的知识,你能设计一个方案,以便分开电荷量相同、质量不同的带电粒子吗?
一、质谱仪
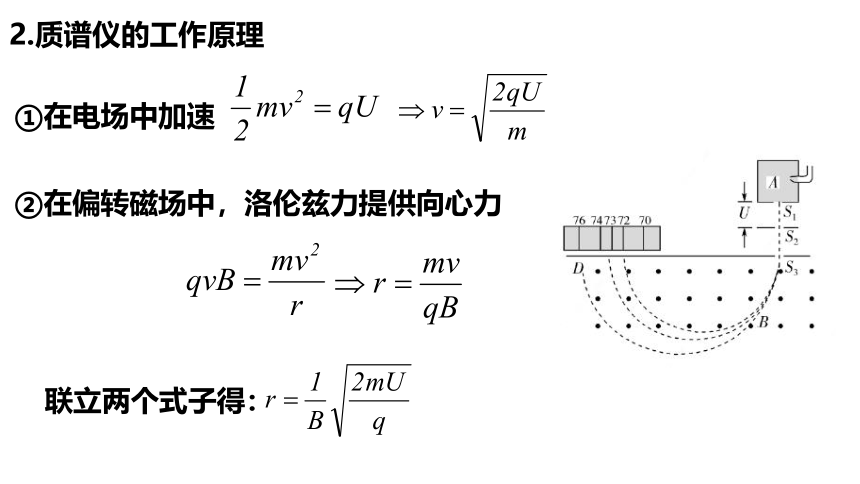
1.质谱仪的基本结构
离子源
加速电场U
偏转磁场B
照相底片
2.质谱仪的工作原理
①在电场中加速
②在偏转磁场中,洛伦兹力提供向心力
联立两个式子得:
③在偏转磁场中,偏转的距离为x
x
x=2r
④由上式可得粒子的质量和比荷
质谱仪是测量带电粒子的质量和分析同位素的重要工具。如图所示为质谱仪的原理示意图,现利用质谱仪对氢元素进行测量。让氢的三种同位素的离子流从容器A下方的小孔S无初速度飘入电势差为U的加速电场,加速后垂直进入磁感应强度为B的匀强磁场中、氢的三种同位素分别为氕(即为质子)、氘(质量约为质子的2倍,电荷量与质子相同)、氚(质量约为质子的3倍,电荷量与质子相同),最后打在照相底片D上,形成a、b、c三条“质谱线”。则下列判断正确的是( )
A.进入磁场时速度从大到小排列的顺序是氕、氘、氚
B.进入磁场时动能从大到小排列的顺序是氕、氘、氚
C.在磁场中运动时间由大到小排列的顺序是氕、氘、氚
D.a、b、c三条“质谱线”依次排列的顺序是氕、氘、氚
A
质谱仪的原理如图所示,由加速电场和偏转磁场组成,虚线AD上方区域存在垂直纸面向外的匀强磁场。同位素离子源产生a、b两种电荷量相同的离子,无初速度进入加速电场,经同一电压加速后,垂直进入磁场,a离子恰好打在C点,b离子恰好打在D点。离子重力不计。则( )
A.两个离子均为负离子
B.a离子质量比b离子质量小
C.a、b离子在磁场中的运动时间相等
D.若增大加速电场的电压U,则两离子在偏转
磁场中运动的半径都变大
BD
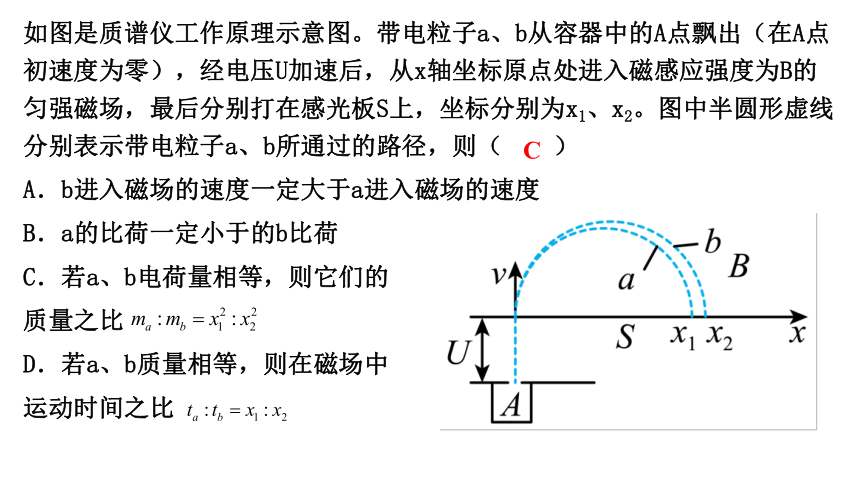
如图是质谱仪工作原理示意图。带电粒子a、b从容器中的A点飘出(在A点初速度为零),经电压U加速后,从x轴坐标原点处进入磁感应强度为B的匀强磁场,最后分别打在感光板S上,坐标分别为x1、x2。图中半圆形虚线分别表示带电粒子a、b所通过的路径,则( )
A.b进入磁场的速度一定大于a进入磁场的速度
B.a的比荷一定小于的b比荷
C.若a、b电荷量相等,则它们的
质量之比
D.若a、b质量相等,则在磁场中
运动时间之比
C
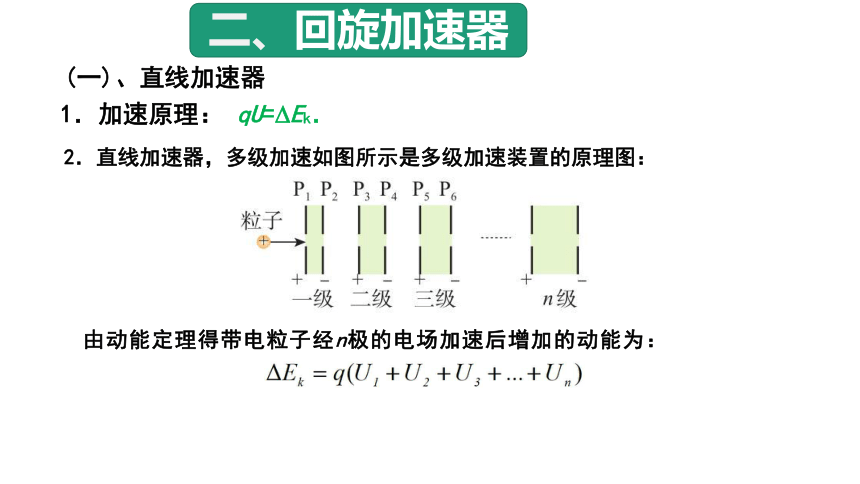
1.加速原理: qU= Ek.
2.直线加速器,多级加速如图所示是多级加速装置的原理图:
(一)、直线加速器
由动能定理得带电粒子经n极的电场加速后增加的动能为:
二、回旋加速器
有的长达几十千米,坐落在两个城市之间……
了解劳伦斯
劳伦斯(Ernest Orlando Rawrence)是美国著名物理学家、回旋加速器的发明者,1901年8月8日出生于美国达科他州南部的坎顿,是一个教书世家,其祖父及父母都是教师,他年仅30岁就闻名于全世界。1930年,劳伦斯受聘于伯克利加利福尼亚大学担任物理学教授。为了研究核物理,劳伦斯提出一种使粒子作曲线运动并同时加速的方案。因人工放射性方面的成果于1939年获诺贝尔物理学奖。1940年,劳伦斯成为麻省理工学院内的另一辐射实验室的美国物理学家之一。在他的实验室中工作过的人,有八人获诺贝尔奖的殊荣,其中四人是劳伦斯的徒弟或低级合作者,另外四人则是以别的方式同“辐射实验室”有联系的。
此加速器可将质子和氘核加速到1MeV的能量,为此1939年劳伦斯获得诺贝尔物理学奖.
1932年劳伦斯研制第一台回旋加速器的D型室.
2.回旋加速器
①基本结构
粒子源
接交流电源
金属盒内部的电场为零
D形盒
②工作原理
正电
A0
v0
A/2
v1
A1
A/1
A2
v2
粒子就会不断的加速
a、粒子源发出粒子
b、在磁场中做半个周期的匀速圆周运动
c、在电场中加速
①带电粒子在D形盒中运行的周期:
(1)加速条件
②每过 电场方向要改变一次,以保证带电粒子始终被加速。
③电场的周期 粒子在磁场圆运动的周期
与速度无关,故周期始终不变。
等于
粒子半径多大时飞出D形盒?
D形盒半径为R
r=R
最大速度
最大动能
(2)粒子最大动能:
对某种粒子q、m一定,粒子获得的最大动能与?有关,
与?无关。
由B 、 D形盒半径R 决定
与加速度电压的大小无关
这个过程看似可以一直进行下去,但实际上由于相对论的效应,粒子的质量会随着速度增,圆周运动的周期也增加,这样电场于运动不在同步,也就没办法加速了。
(3)回旋加速器不可无限加速。
粒子速度v接近光速c时,质量变大,在磁场中运动周期改变,与交变电场周期不同步。
改进:
所以加速次数:
所以加速总时间:
如已知加速电压为U,忽略在电场中运动时间,求加速的次数和加速的总时间。
解:每次加速得到的动能
EK=qU
由于圆周运动的周期:
真空中的D形金属盒半径为R,两盒间狭缝间距为d,磁感应强度为B的匀强磁场与盒面垂直,被加速粒子m、+q,加在狭缝间的交变电压U0,周期T= 。t=0时刻初速度视为零从A处进入电场。现考虑粒子在狭缝中的运动时间,假设能够出射的粒子每次经过狭缝均做加速运动,不考虑粒子间的相互作用。求:
(1)出射粒子的动能Em;
离子在磁场中做匀速圆周运动:
(2)粒子在回旋加速器中运动的总时间。
(2)粒子运动存在于两个空间,一是狭缝间电场力使之做匀加速运动,二是D形金属盒中洛伦兹力使之做匀速圆周运动。粒子在狭缝间的运动可等效成连续的匀加速直线运动,根据最大动能可求得加速的时间;根据最大动能可求得加速的次数,从而求得粒子做完整圆周运动的次数,进而求得粒子圆周运动的时间。
所以粒子运动的总时间:
设粒子被加速n次达到动能Em
则Em=nqU0,解得
粒子在狭缝间的运动可等效成匀加速直线运动,设n次经过狭缝的总时间为Δt
粒子做圆周运动的总时间
则:
又:
即:
1.在磁场中做圆周运动,周期不变
2.每一个周期加速两次
3.电场的周期与粒子在磁场中做圆周运动周期相同
4.电场一个周期中方向变化两次
5.粒子加速的最大速度由盒的半径决定(BR共同决定,与电压无关)
6.电场加速过程中,时间极短,一般可忽略(电压决定加速次数)
4.回旋加速器的特点总结
——同步加速器
法国东南部格勒诺布尔
我国首台超导回旋加速器
如图所示,回旋加速器D形盒的半径为R,用来加速质量为m,电量为q的质子,质子每次经过电场区时,都恰好在电压为U时被加速,且电场可视为匀强电场,使质子由静止加速到能量为E后,由A孔射出。下列说法正确的是( )
A.D形盒半径R、磁感应强度B不变,若加速电压U越高,
质子的能量E将越大
B.磁感应强度B不变,若加速电压U不变,D形盒半径R越大,
质子的能量E将越大
C.D形盒半径R、磁感应强度B不变,若加速电压U越高,
质子在加速器中的运动时间将越长
D.D形盒半径R、磁感应强度B不变,若加速电压U越高,
质子在加速器中的运动时间将越短
BD
如图为回旋加速器的示意图,两个靠得很近的D形金属盒处在与盒面垂直的匀强磁场中,磁场的磁感应强度为B,已知D形盒的半径为R,高频交变电源的电压为U、频率为f,质子质量为m,电荷量为q,已知质子在磁场中运动的周期等于交变电源的周期,下列说法正确的是( )
A.粒子由加速器的边缘进入加速器
B.质子的最大速度不超过2πRf
C.质子的最大动能与U无关
D.粒子在狭缝和D形盒中运动时都能获得加速
BC
为回旋加速器的原理图.其中D1和D2是两个中空的半径为R的半圆形金属盒,接在电压为U的加速电源上,位于D2圆心处的粒子源A能不断释放出一种带电粒子(初速度可以忽略,重力不计),粒子在两盒之间被电场加速,D1、D2置于与盒面垂直的磁感应强度为B的匀强磁场中。已知粒子电荷量为q、质量为m,忽略粒子在电场中运动的时间,不考虑加速过程中引起的粒子质量变化,下列说法正确的是( )
A.加速电源可以用直流电源,也可以用任意频率的交流电源
B.加速交流电源的周期为
C.粒子第一次进入D1盒与第一次进入盒D2的半径之比为1:2
D.粒子在电场中加速的次数为
BD
6.如图所示,回旋加速器由两个铜质半圆D形金属盒D1、D2构成,其间留有缝隙,缝隙处接交流电源。D形盒处于匀强磁场中,磁场方向垂直于盒底面,盒的圆心附近置有粒子源,若粒子源射出的粒子带电荷量为q(q>0),质量为m,粒子最大回旋半径为R,下列说法正确的是( )
A.回旋加速器的磁场方向一定做周期性变化
B.粒子被加速后的最大速度随加速电压增大而增大
C.交流电压的周期
D.粒子飞出加速器的动能为
CD
课堂小结
1.质谱仪
①在电场中加速
②在偏转磁场中,洛伦兹力提供向心力
③在偏转磁场中,偏转的距离为
x=2r
④由上式可得粒子的质量和比荷
2.多级直线加速器
①加速原理:在电场中加速,qU = ΔEk。
②缺点:占有的空间范围大
两场周期相等 ( 频率相等)
当粒子做圆周运动的半径与D形盒半径R相同时:
r=R
最大速度
最大动能
加速次数
加速总时间
(忽略电场运动时间)
3.回旋加速器 加速条件 最大速度 加速次数 加速时间
第一章 安培力与洛伦兹力
1.4 质谱仪与回旋加速器
在科学研究和工业生产中,常需要将一束带等量电荷的粒子分开,以便知道其中所含物质的成分。利用所学的知识,你能设计一个方案,以便分开电荷量相同、质量不同的带电粒子吗?
一、质谱仪
1.质谱仪的基本结构
离子源
加速电场U
偏转磁场B
照相底片
2.质谱仪的工作原理
①在电场中加速
②在偏转磁场中,洛伦兹力提供向心力
联立两个式子得:
③在偏转磁场中,偏转的距离为x
x
x=2r
④由上式可得粒子的质量和比荷
质谱仪是测量带电粒子的质量和分析同位素的重要工具。如图所示为质谱仪的原理示意图,现利用质谱仪对氢元素进行测量。让氢的三种同位素的离子流从容器A下方的小孔S无初速度飘入电势差为U的加速电场,加速后垂直进入磁感应强度为B的匀强磁场中、氢的三种同位素分别为氕(即为质子)、氘(质量约为质子的2倍,电荷量与质子相同)、氚(质量约为质子的3倍,电荷量与质子相同),最后打在照相底片D上,形成a、b、c三条“质谱线”。则下列判断正确的是( )
A.进入磁场时速度从大到小排列的顺序是氕、氘、氚
B.进入磁场时动能从大到小排列的顺序是氕、氘、氚
C.在磁场中运动时间由大到小排列的顺序是氕、氘、氚
D.a、b、c三条“质谱线”依次排列的顺序是氕、氘、氚
A
质谱仪的原理如图所示,由加速电场和偏转磁场组成,虚线AD上方区域存在垂直纸面向外的匀强磁场。同位素离子源产生a、b两种电荷量相同的离子,无初速度进入加速电场,经同一电压加速后,垂直进入磁场,a离子恰好打在C点,b离子恰好打在D点。离子重力不计。则( )
A.两个离子均为负离子
B.a离子质量比b离子质量小
C.a、b离子在磁场中的运动时间相等
D.若增大加速电场的电压U,则两离子在偏转
磁场中运动的半径都变大
BD
如图是质谱仪工作原理示意图。带电粒子a、b从容器中的A点飘出(在A点初速度为零),经电压U加速后,从x轴坐标原点处进入磁感应强度为B的匀强磁场,最后分别打在感光板S上,坐标分别为x1、x2。图中半圆形虚线分别表示带电粒子a、b所通过的路径,则( )
A.b进入磁场的速度一定大于a进入磁场的速度
B.a的比荷一定小于的b比荷
C.若a、b电荷量相等,则它们的
质量之比
D.若a、b质量相等,则在磁场中
运动时间之比
C
1.加速原理: qU= Ek.
2.直线加速器,多级加速如图所示是多级加速装置的原理图:
(一)、直线加速器
由动能定理得带电粒子经n极的电场加速后增加的动能为:
二、回旋加速器
有的长达几十千米,坐落在两个城市之间……
了解劳伦斯
劳伦斯(Ernest Orlando Rawrence)是美国著名物理学家、回旋加速器的发明者,1901年8月8日出生于美国达科他州南部的坎顿,是一个教书世家,其祖父及父母都是教师,他年仅30岁就闻名于全世界。1930年,劳伦斯受聘于伯克利加利福尼亚大学担任物理学教授。为了研究核物理,劳伦斯提出一种使粒子作曲线运动并同时加速的方案。因人工放射性方面的成果于1939年获诺贝尔物理学奖。1940年,劳伦斯成为麻省理工学院内的另一辐射实验室的美国物理学家之一。在他的实验室中工作过的人,有八人获诺贝尔奖的殊荣,其中四人是劳伦斯的徒弟或低级合作者,另外四人则是以别的方式同“辐射实验室”有联系的。
此加速器可将质子和氘核加速到1MeV的能量,为此1939年劳伦斯获得诺贝尔物理学奖.
1932年劳伦斯研制第一台回旋加速器的D型室.
2.回旋加速器
①基本结构
粒子源
接交流电源
金属盒内部的电场为零
D形盒
②工作原理
正电
A0
v0
A/2
v1
A1
A/1
A2
v2
粒子就会不断的加速
a、粒子源发出粒子
b、在磁场中做半个周期的匀速圆周运动
c、在电场中加速
①带电粒子在D形盒中运行的周期:
(1)加速条件
②每过 电场方向要改变一次,以保证带电粒子始终被加速。
③电场的周期 粒子在磁场圆运动的周期
与速度无关,故周期始终不变。
等于
粒子半径多大时飞出D形盒?
D形盒半径为R
r=R
最大速度
最大动能
(2)粒子最大动能:
对某种粒子q、m一定,粒子获得的最大动能与?有关,
与?无关。
由B 、 D形盒半径R 决定
与加速度电压的大小无关
这个过程看似可以一直进行下去,但实际上由于相对论的效应,粒子的质量会随着速度增,圆周运动的周期也增加,这样电场于运动不在同步,也就没办法加速了。
(3)回旋加速器不可无限加速。
粒子速度v接近光速c时,质量变大,在磁场中运动周期改变,与交变电场周期不同步。
改进:
所以加速次数:
所以加速总时间:
如已知加速电压为U,忽略在电场中运动时间,求加速的次数和加速的总时间。
解:每次加速得到的动能
EK=qU
由于圆周运动的周期:
真空中的D形金属盒半径为R,两盒间狭缝间距为d,磁感应强度为B的匀强磁场与盒面垂直,被加速粒子m、+q,加在狭缝间的交变电压U0,周期T= 。t=0时刻初速度视为零从A处进入电场。现考虑粒子在狭缝中的运动时间,假设能够出射的粒子每次经过狭缝均做加速运动,不考虑粒子间的相互作用。求:
(1)出射粒子的动能Em;
离子在磁场中做匀速圆周运动:
(2)粒子在回旋加速器中运动的总时间。
(2)粒子运动存在于两个空间,一是狭缝间电场力使之做匀加速运动,二是D形金属盒中洛伦兹力使之做匀速圆周运动。粒子在狭缝间的运动可等效成连续的匀加速直线运动,根据最大动能可求得加速的时间;根据最大动能可求得加速的次数,从而求得粒子做完整圆周运动的次数,进而求得粒子圆周运动的时间。
所以粒子运动的总时间:
设粒子被加速n次达到动能Em
则Em=nqU0,解得
粒子在狭缝间的运动可等效成匀加速直线运动,设n次经过狭缝的总时间为Δt
粒子做圆周运动的总时间
则:
又:
即:
1.在磁场中做圆周运动,周期不变
2.每一个周期加速两次
3.电场的周期与粒子在磁场中做圆周运动周期相同
4.电场一个周期中方向变化两次
5.粒子加速的最大速度由盒的半径决定(BR共同决定,与电压无关)
6.电场加速过程中,时间极短,一般可忽略(电压决定加速次数)
4.回旋加速器的特点总结
——同步加速器
法国东南部格勒诺布尔
我国首台超导回旋加速器
如图所示,回旋加速器D形盒的半径为R,用来加速质量为m,电量为q的质子,质子每次经过电场区时,都恰好在电压为U时被加速,且电场可视为匀强电场,使质子由静止加速到能量为E后,由A孔射出。下列说法正确的是( )
A.D形盒半径R、磁感应强度B不变,若加速电压U越高,
质子的能量E将越大
B.磁感应强度B不变,若加速电压U不变,D形盒半径R越大,
质子的能量E将越大
C.D形盒半径R、磁感应强度B不变,若加速电压U越高,
质子在加速器中的运动时间将越长
D.D形盒半径R、磁感应强度B不变,若加速电压U越高,
质子在加速器中的运动时间将越短
BD
如图为回旋加速器的示意图,两个靠得很近的D形金属盒处在与盒面垂直的匀强磁场中,磁场的磁感应强度为B,已知D形盒的半径为R,高频交变电源的电压为U、频率为f,质子质量为m,电荷量为q,已知质子在磁场中运动的周期等于交变电源的周期,下列说法正确的是( )
A.粒子由加速器的边缘进入加速器
B.质子的最大速度不超过2πRf
C.质子的最大动能与U无关
D.粒子在狭缝和D形盒中运动时都能获得加速
BC
为回旋加速器的原理图.其中D1和D2是两个中空的半径为R的半圆形金属盒,接在电压为U的加速电源上,位于D2圆心处的粒子源A能不断释放出一种带电粒子(初速度可以忽略,重力不计),粒子在两盒之间被电场加速,D1、D2置于与盒面垂直的磁感应强度为B的匀强磁场中。已知粒子电荷量为q、质量为m,忽略粒子在电场中运动的时间,不考虑加速过程中引起的粒子质量变化,下列说法正确的是( )
A.加速电源可以用直流电源,也可以用任意频率的交流电源
B.加速交流电源的周期为
C.粒子第一次进入D1盒与第一次进入盒D2的半径之比为1:2
D.粒子在电场中加速的次数为
BD
6.如图所示,回旋加速器由两个铜质半圆D形金属盒D1、D2构成,其间留有缝隙,缝隙处接交流电源。D形盒处于匀强磁场中,磁场方向垂直于盒底面,盒的圆心附近置有粒子源,若粒子源射出的粒子带电荷量为q(q>0),质量为m,粒子最大回旋半径为R,下列说法正确的是( )
A.回旋加速器的磁场方向一定做周期性变化
B.粒子被加速后的最大速度随加速电压增大而增大
C.交流电压的周期
D.粒子飞出加速器的动能为
CD
课堂小结
1.质谱仪
①在电场中加速
②在偏转磁场中,洛伦兹力提供向心力
③在偏转磁场中,偏转的距离为
x=2r
④由上式可得粒子的质量和比荷
2.多级直线加速器
①加速原理:在电场中加速,qU = ΔEk。
②缺点:占有的空间范围大
两场周期相等 ( 频率相等)
当粒子做圆周运动的半径与D形盒半径R相同时:
r=R
最大速度
最大动能
加速次数
加速总时间
(忽略电场运动时间)
3.回旋加速器 加速条件 最大速度 加速次数 加速时间
